The $\epsilon \to 0$ Limit

In a previously mentioned paper [9] it was shown that the first-order linear low-pass filter, in its real form, tends to the identity operator almost everywhere in the $\epsilon \to 0$ limit. In Section 6 of Appendix A of that paper one can find a simple proof that in this limit the filtered function reproduces the value of the original function whenever that function is continuous, that is

$$\lim_{\epsilon\to 0} f_{\epsilon}(\theta) = f(\theta),$$

which holds at every point where $f(\theta)$ is continuous. At isolated points of discontinuity where the two lateral limits of the original function to the point of discontinuity exist, the filtered function converges, in the $\epsilon \to 0$ limit, to the average of the two lateral limits, as shown in Section 7 of that same Appendix,

$$\lim_{\varepsilon\to 0}f_{\varepsilon}(\theta_{0}) = \frac{1}{2}\left({\cal L}_{\oplus}+{\cal L}_{\ominus}\right),$$

where

$$\begin{eqnarray*} {\cal L}_{\oplus} & = & \hspace{-1em} \lim_{\hspace{0.8em}... ...space{-1em} \lim_{\hspace{0.8em}\theta\to\theta_{0-}}f(\theta). \end{eqnarray*}$$

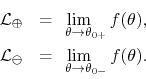
When the two limits coincide, and therefore the original function is continuous at the point $\theta_{0}$, this of course reduces to the previous property. At isolated points of non-differentiability where the two lateral limits to that point of the derivative of the original function exist, the derivative of the filtered function converges, in the $\epsilon \to 0$ limit, to the average of these two lateral limits, as shown in Section 8 of that same Appendix,

$$\lim_{\varepsilon\to 0} \frac{df_{\varepsilon}}{d\theta}(\... ...frac{1}{2}\left({\cal L'}_{\oplus}+{\cal L'}_{\ominus}\right),$$

where

$$\begin{eqnarray*} {\cal L'}_{\oplus} & = & \hspace{-1em} \lim_{\hspace{0.8em... ..._{\hspace{0.8em}\theta\to\theta_{0-}}\frac{df}{d\theta}(\theta). \end{eqnarray*}$$

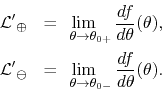
Of course, this implies that, at points where the function $f(\theta)$ is differentiable, the derivative of the filtered function converges, in the $\epsilon \to 0$ limit, to the derivative of the original function. From all this we may conclude that, so long as there is only a finite number of singular points, or at most an infinite but zero-measure set of such points, in the $\epsilon \to 0$ limit the real filter becomes the identity operator almost everywhere.

In addition to this, one can easily prove that the corresponding complex filter always becomes exactly the identity operator in the $\epsilon \to 0$ limit, within the open unit disk. This was commented on in [3], but since it is quite crucial to our current argument let us repeat the demonstration here. We can see this from the complex-plane definition in Equation (4). If we consider the variation of $\theta$ between the extremes $z_{\oplus }$ and $z_{\ominus }$, which is given in terms of the parameter $\epsilon$ by $\delta\theta=2\epsilon$, and we take the $\epsilon \to 0$ limit of that expression, we get

$$\begin{eqnarray*} \lim_{\epsilon\to 0} w_{\epsilon}(z) & = & -\mbox{\boldmat... ...\oplus})-w^{-1\!\mbox{\Large$\cdot$}\!}(z_{\ominus})}{\delta z}, \end{eqnarray*}$$

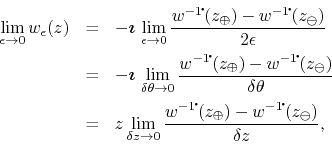
where we used the fact that in the limit $\delta z=\mbox{\boldmath$\imath$}z\delta\theta$. Since we have that $\delta z=z_{\oplus}-z_{\ominus}$, we see that the limit above defines the logarithmic derivative of $w^{-1\!\mbox{\Large$\cdot$}\!}(z)$. In addition to this, since that function is analytic in the open unit disk, the limit necessarily exists. Therefore, we have

$$\begin{eqnarray*} \lim_{\epsilon\to 0} w_{\epsilon}(z) & = & z\, \frac{d}{dz}w^{-1\!\mbox{\Large$\cdot$}\!}(z) \\ & = & w(z), \end{eqnarray*}$$

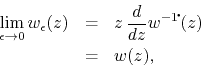
since we have here the logarithmic derivative of the logarithmic primitive, and the operations of logarithmic differentiation and logarithmic integration are the inverses of one another, as shown in [2]. We see, therefore, that this property within the open unit disk is stronger than the corresponding property on the unit circle, since in this case we have exactly the identity in all cases, while in the real case we had only the identity almost everywhere. We have therefore that, for all inner analytic functions $w(z)$,

$$\lim_{\epsilon\to 0}w_{\epsilon}(z) = w(z),$$

which holds in the whole open unit disk. Since every inner analytic function, filtered or not, corresponds to a real generalized function on the unit circle in the $\rho\to 1$ limit, defined at all points where this limit exists, the one-parameter family of inner analytic functions $w_{\epsilon}(z)$ corresponds to a one-parameter family of real generalized functions $f_{\epsilon}(\theta)$ on the unit circle. It is therefore clear that as $w_{\epsilon}(z)$ approaches $w(z)$ in the $\epsilon \to 0$ limit, so does $f_{\epsilon}(\theta)$ approach $f(\theta)$ in that same limit, at all points of the unit circle where the $\rho\to 1$ limit exists, that is, at least almost everywhere.