The Low-Pass Filters

Consider a real function $f(\theta)$ defined within the periodic interval $[-\pi,\pi]$, or equivalently on the unit circle. In this paper we assume that all real functions to be discussed are Lebesgue-measurable functions [10]. Let us recall that for Lebesgue-measurable real functions defined within a compact domain the conditions of integrability, absolute integrability and local integrability are all equivalent to one another, as discussed in [5]. The real functions we are to deal with here may be integrable in the whole domain, or they may be what we call locally non-integrable, as defined in [5]. This means that they are not integrable on the whole domain, but are integrable in all closed sub-intervals of the domain that do not contain any of the non-integrable singular points of the function, of which we assume there is at most a finite number. Therefore the term ``locally non-integrable'' is to be understood as meaning ``locally integrable almost everywhere''. An integrable singularity is one around which the asymptotic integral of the function exists, while around a non-integrable one the asymptotic integral does not exist, or diverges to infinity.

Figure 1: Illustration of the definition of the complex first-order linear low-pass filter within the unit disk of the complex plane. The integral giving the average is taken over the arc of circle from $z_{\ominus }$ to $z_{\oplus }$. The points $z_{\ominus }$, $z_{\oplus }$ and $0$ form a closed contour.

For such functions we may define the action of the first-order linear low-pass filter as an operator acting on the space of real functions, which from the real function $f(\theta)$ produces another real function $f_{\epsilon}(\theta)$ by means of the integral

$$f_{\epsilon}(\theta) = \frac{1}{2\epsilon} \int_{\theta-\epsilon}^{\theta+\epsilon}d\theta'\, f\!\left(\theta'\right),$$ (1)

which is well-defined at the point $\theta$ so long as the interval $[\theta-\epsilon,\theta+\epsilon]$ does not contain any of the non-integrable singularities of the original function. Since we are on the unit circle, the parameter $\epsilon$ must satisfy $0<\epsilon\leq\pi$. In this paper we will be interested mostly in the limit $\epsilon \to 0$, and in this limit this definition suffices to determine $f_{\epsilon}(\theta)$ at all points except for the non-integrable singular points of $f(\theta)$, that is to say almost everywhere, and strictly everywhere within the domain of definition of $f(\theta)$ itself. The low-pass filter can also be defined in terms of an integration kernel $K_{\epsilon}\!\left(\theta-\theta'\right)$,

$$f_{\epsilon}(\theta) = \int_{-\pi}^{\pi}d\theta'\, K_{\epsilon}\!\left(\theta-\theta'\right) f\!\left(\theta'\right),$$

where the kernel is defined as

$$% \renewedcommand{arraystretch}{2.0} \begin{array}{rclcc... ... & \left\vert\theta-\theta'\right\vert>\epsilon. \end{array}$$

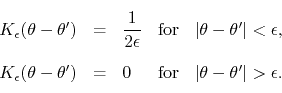
As was shown in [3], this real operator acting on the real functions can be obtained from a corresponding complex operator acting on the inner analytic functions, in the limit from the open unit disk to the unit circle, as follows. Consider an inner analytic function $w(z)$, with $z=\rho\exp(\mbox{\boldmath$\imath$}\theta)$ and $0\leq\rho\leq 1$. We define from it the corresponding filtered complex function $w_{\epsilon}(z)$, using the real angular range parameter $0<\epsilon\leq\pi$, by

$$w_{\epsilon}(z) = -\, \frac{\mbox{\boldmath$\imath$}}{2\... ...minus}}^{z_{\oplus}}dz'\, \frac{1}{z'}\, w\!\left(z'\right),$$ (2)

involving an integral over the arc of circle illustrated in Figure 1, where the two extremes are given by

$$\begin{eqnarray*} z_{\ominus} & = & z\,{\rm e}^{-\mbox{\boldmath$\imath$}\eps... ... = & \rho\,{\rm e}^{\mbox{\boldmath$\imath$}(\theta+\epsilon)}. \end{eqnarray*}$$

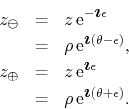
This definition can be implemented at all the points of the open unit disk. Note that if we make $z\to 0$, the integrand in Equation (2) converges to a finite number, since the Taylor series of $w(z)$ around $z=0$ has no constant term, given that $w(z)$ is an inner analytic function. It follows that in that limit the integral converges to zero, because the domain of integration becomes a single point in the limit. Therefore we conclude that $w_{\epsilon}(0)=0$, which means that the filter reduces to the local identity at $z=0$. Since on the arc of circle we have that $z'=\rho\exp(\mbox{\boldmath$\imath$}\theta')$ and hence that $dz'=\mbox{\boldmath$\imath$}z'd\theta'$, we may also write the definition of the complex filtered function as

$$w_{\epsilon}(z) = \frac{1}{2\epsilon} \int_{\theta-\epsilon}^{\theta+\epsilon}d\theta'\, w\!\left(\rho,\theta'\right),$$ (3)

which makes it explicitly clear that what we have here is a simple normalized integral over $\theta$. One can thus see that what we are doing is to map the value of the function $w(z)$ at $z$ to the average of $w(z)$ over the symmetric arc of circle of angular span $2\epsilon$ around $z$, with constant $\rho$. This defines a new complex function $w_{\epsilon}(z)$ at that point.

Repeating what was done in [3] in the context of the old-style inner analytic functions, and since it is a crucial part of our present argument, let us now show that this complex function is in fact analytic, and therefore that it is an inner analytic function according to the newer definition given in [5], since we have already shown that it has the property that $w_{\epsilon}(0)=0$. The definition in Equation (2) has the general form of a logarithmic integral, which is the inverse operation to the logarithmic derivative, as defined and discussed in [2], where the logarithmic primitive of $w(z)$ was defined as the integral

$$w^{-1\!\mbox{\Large$\cdot$}\!}(z) = \int_{0}^{z}dz'\, \frac{1}{z'}\, w\!\left(z'\right),$$

over any simple curve from $z'=0$ to $z'=z$ within the open unit disk, and where we are using the notation for the logarithmic primitive introduced in that paper. The logarithmic primitive $w^{-1\!\mbox{\Large$\cdot$}\!}(z)$ is an analytic function within the open unit disk, as shown in [2], and it clearly has the property that $w^{-1\!\mbox{\Large$\cdot$}\!}(0)=0$, so that it is an inner analytic function as well. In order to demonstrate the analyticity of $w_{\epsilon}(z)$ we consider the integral over the closed positively-oriented circuit shown in Figure 1, from which it follows that we have

$$\int_{0}^{z_{\ominus}}dz'\, \frac{1}{z'}\, w\!\left(z'\ri... ..._{\oplus}}^{0}dz'\, \frac{1}{z'}\, w\!\left(z'\right) = 0,$$

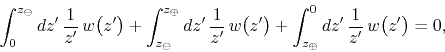
due to the Cauchy-Goursat theorem, since the contour is closed and the integrand is analytic on it and within it. It follows that we have

$$\int_{z_{\ominus}}^{z_{\oplus}}dz'\, \frac{1}{z'}\, w\!\l... ...}(z_{\oplus}) - w^{-1\!\mbox{\Large$\cdot$}\!}(z_{\ominus}).$$

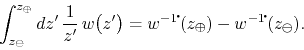
Since the logarithmic primitive $w^{-1\!\mbox{\Large$\cdot$}\!}(z)$ is an analytic function within the open unit disk, and since the functions $z_{\ominus}(z)$ and $z_{\oplus}(z)$ are also analytic functions in that domain, it follows that the right-hand side of this equation is an analytic function of $z$ within the open unit disk. We have therefore for the filtered complex function

$$w_{\epsilon}(z) = -\, \frac{\mbox{\boldmath$\imath$}}{2\... ...us}) - w^{-1\!\mbox{\Large$\cdot$}\!}(z_{\ominus}) \right],$$ (4)

which shows that $w_{\epsilon}(z)$ is an analytic function as well. Since we have already shown that $w_{\epsilon}(0)=0$, it follows that this complex filtered function is an inner analytic function.

Let us now show that this complex low-pass filter reduces to the real low-pass filter on the unit circle. If we write both the original function $w(z)$ and the filtered function $w_{\epsilon}(z)$ in terms of their real and imaginary parts, the expression in Equation (3) becomes

$$\left[ f_{\epsilon}(\rho,\theta) + \mbox{\boldmath$\imat... ...oldmath$\imath$} \bar{f}\!\left(\rho,\theta'\right) \right],$$

where $\bar{f}_{\epsilon}(\rho,\theta)$ and $\bar{f}(\rho,\theta)$ are the harmonic conjugate functions respectively of $f_{\epsilon}(\rho,\theta)$ and $f(\rho,\theta)$. If we now take the $\rho\to 1$ limit to the unit circle, we get from the real and imaginary parts of this expression

$$\begin{eqnarray*} f_{\epsilon}(1,\theta) & = & \frac{1}{2\epsilon} \int_{\th... ...n}^{\theta+\epsilon}d\theta'\, \bar{f}\!\left(1,\theta'\right), \end{eqnarray*}$$

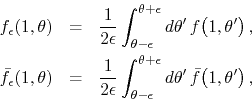
so long as the integration interval on the unit circle does not contain any non-integrable singularities of $w(z)$. Since the real part $f_{\epsilon}(\rho,\theta)$ of $w_{\epsilon}(z)$ tends in the $\rho\to 1$ limit to the real generalized function $f_{\epsilon}(\theta)$ corresponding to the inner analytic function $w_{\epsilon}(z)$, we may conclude that in the $\rho\to 1$ limit the complex filter reduces to the definition of the real filter given in Equation (1), for any real generalized function $f(\theta)=f(1,\theta)$ that can be obtained as the $\rho\to 1$ limit of the real part of an inner analytic function. The same is true for the imaginary part, of course, which converges to the corresponding ``Fourier Conjugate'' real generalized function, a concept which was defined in [1] and restated in [5].