Analytical Character of the Limits

It is interesting that one may establish without too much difficulty at least one analytical property of the functions to which the class of Fourier series studied here converge, which is related to their continuity over the unit circle. For simplicity, let us limit this discussion to the simplest type of series, the one which we discussed in detail in this paper. However, there should be no difficulty in extending the ideas to the generalizations mentioned before.

First let us observe that, for series of bounded functions such as the complex basis $v^{k}=\exp(\mbox{\boldmath$\imath$}k\theta)$, for which the modulus of each function is unity, and hence independent of the variable $\theta$, absolute convergence implies convergence with criteria which do not depend on the variable $\theta$, and therefore imply uniform convergence. This can also be established by the use of the Weierstrass $M$-test. Hence, given any closed interval of the unit circle which does not contain the special point $\theta=0$, for which $v=1$, the series in the following expression for $S(\theta)$,

$$S(\theta) = \frac{1}{1-v} \sum_{k=0}^{\infty}b_{k}v^{k},$$

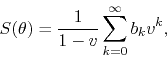
is uniformly convergent within that interval. Therefore, using the well-known fact that a series of continuous functions which converges uniformly over a closed interval does so to a continuous function, it follows that the series converges to a continuous function within that interval. This implies that the whole class of Fourier series discussed here, in this simplest case, converge to continuous functions, everywhere except for the special point $\theta=0$ over the unit circle. It is clear that similar properties hold for the extensions of the theorem in which there are several such special points.

However, the differentiability properties of these functions are not so easily determined. Since the series in the right-hand side is absolutely and hence uniformly convergent, it may be possible to differentiate it term-by-term to produce a convergent series, even if one certainly cannot do the same to the original series for $S(\theta)$, when that series is not absolutely convergent. Using the fact that

$$\frac{\partial v}{\partial \theta} = \mbox{\boldmath$\imath$}v,$$

we may attempt to calculate the derivative of $S(\theta)$, thus obtaining

$$\begin{eqnarray*} \frac{\partial S}{\partial\theta} & = & \frac{\mbox{\boldma... ...mbox{\boldmath$\imath$}}{1-v} \sum_{k=1}^{\infty}k\,b_{k}v^{k}. \end{eqnarray*}$$

The series contained within $S(\theta)$ in the first term is convergent due to our theorem, so the differentiability of the function is related to the convergence or lack of convergence of the series in the second term, which depends on the behavior of the coefficients $c_{k}=k\,b_{k}$. If these coefficients turn out to be such that the corresponding series is absolutely convergent within the closed interval mentioned before, then it follows that the function is differentiable in that interval.

Absolute convergence depends on the coefficients $c_{k}$ going to zero sufficiently fast with $k$, while term-by-term differentiation implies in a factor of $k$ multiplying $b_{k}$. Therefore, while it is possible that some of these functions are continuous, it seems likely that many are not. In fact, since the original series defining $S(\theta)$ may converge very slowly and may contain significant Fourier components for very large frequencies, it does lead to the impression that the limiting functions might not be differentiable at all, undergoing violent high-frequency oscillations everywhere. At first glance it certainly seems very unlikely that these functions may have more than the first derivative, due to the increasing powers of $k$ multiplying $b_{k}$, which are implied by multiple term-by-term differentiation.

However, there is another possibility, namely that the coefficients $c_{k}$ turn out to also satisfy the hypotheses of our theorem. In this case one would be able to transform the corresponding series once more into one which is absolutely convergent, which would then imply the differentiability of the function. For cases in which this procedure can be iterated, it might be possible to show that the functions also have the second derivative, or even higher-order ones. The crucial hypothesis is that of the monotonicity of $c_{k}$, and that depends essentially on the monotonicity of $b_{k}$. If there are series for which the transformation from $a_{k}$ to $b_{k}$ preserves the monotonic character of the sequence, then these series should converge to functions which are differentiable in the closed interval mentioned above.

Conceivably, there might even exist series for which this procedure of the transformation of the coefficients can be iterated indefinitely. In such a case the limiting functions would turn out to be infinitely differentiable within the closed interval, that is, of class ${\cal C}^{\infty}$. We must conclude, therefore, that the differentiability properties of these functions remain as completely open questions.