Final Comments

The result demonstrated here may constitute an useful tool for those who need to use Fourier series in their work, particularly in the solution of boundary value problems in the theory and the applications of partial differential equations. However, at least two interesting questions remain as open problems. One is of practical interest, and regards the issue of how to recognize, in general, when a given series can be decomposed as a finite sum of series with coefficients which satisfy our hypotheses.

Another question, of a more theoretical interest, is whether or not one can cover all possible convergent Fourier series with some form of decomposition in series such as those we studied here. In other words, whether or not there is a convergent Fourier series which is not absolutely convergent and cannot be so decomposed. This may constitute a new path of exploration for the old quest for a necessary and sufficient condition for the convergence of Fourier series to limiting functions.

It also is interesting that the theorem gives rise to the possibility of some numerical and possibly also symbolical experimentation with the construction of functions, via the evaluation of the limits of series which converge extremely slowly. Using the series with the $b_{k}$ coefficients, the limits can be easily evaluated, but the corresponding $S(\theta)$ functions, as defined by the series with the $a_{k}$ coefficients, will have significant components for very large frequencies. For example, one could consider further probing into the analytical nature of the limit of the series

$$S(\theta) = \sum_{k=1}^{\infty}\frac{v^{k}}{k^{p}},$$

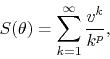
for small positive values of $p$, typically $p<1$, but preferably much smaller positive numbers. In particular, it would be interesting to determine whether or not there are any weakly-convergent Fourier series of this type which converge to ${\cal C}^{\infty}$ functions.

Finally, due to the question of the order of summation of series which are not absolutely convergent, and to the fact that a particular order was implicitly chosen in some of the extensions of the theorem which were discussed before, it may be interesting to examine more carefully these extensions, possibly aiming at the formulation of more precise proofs when appropriate.