Extension of the Result to Other Cases

The result demonstrated here, which we may refer to as the monotonicity convergence criterion, can be readily extended to some other cases, which are easily related to the one we examined in detail above. First of all, the condition that the coefficients $a_{n}$ decrease monotonically to zero need not apply to the whole sequence. It is enough if it holds for all $n$ above a certain minimum value $n_{0}$, because the sum up to this value $n_{0}$ is a finite sum and hence there are no convergence issues for this initial part of the complete sum. Also, it is obvious that we may exchange the overall sign of the series and still have the result hold true, so that the coefficients may as well be monotonically increasing to zero from negative values.

Some other extensions are a bit less obvious. A particularly interesting one is that in which all coefficients with a certain parity of $k$ are zero, while the others approach zero monotonically. For example, if the coefficients are only non-zero for $k=2j$, then the partial sums are given by

$$S_{n}(\theta) = \sum_{j=0}^{n}a_{2j}e^{\mbox{\boldmath$\imath$}2j\theta}.$$

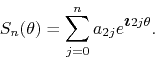
If we consider the angle $\theta'=2\theta$ and rename the coefficients as $a'_{j}=a_{2j}$, we may write this as

$$S_{n}(\theta') = \sum_{j=0}^{n}a'_{j}e^{\mbox{\boldmath$\imath$}j\theta'},$$

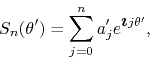
which has exactly the same structure as the case examined before, with only trivial differences in the names of the symbols. If we adopt $v=\exp(\mbox{\boldmath$\imath$}\theta')$, we may write

$$S_{n}(\theta') = \sum_{k=0}^{n}a'_{k}v^{k}.$$

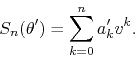
Therefore, so long as the coefficients $a'_{k}$ approach zero monotonically when $k\to\infty$, the result holds for this type of series as well. The only significant difference is that, since $\theta'$ has as its domain the periodic interval $[-2\pi,2\pi]$, there are now two special points, where the exceptional case $v=1$ applies, $\theta'=0$ and $\theta'=2\pi$, corresponding to $\theta=0$ and $\theta=\pi$. At these points the sine series will converge to a discontinuous function, while the cosine series will diverge, when the complex series is not absolutely convergent. On can easily see this because at $\theta=0$ and $\theta=\pi$ we have $\sin(k\theta)=0$ for all $k$, and therefore the sine series converges to zero, while at at $\theta=0$ we have $\cos(k\theta)=1$ for all $k$, and at $\theta=\pi$ we have $\cos(k\theta)=1$ for all terms of the series because $k$ is even, so that the cosine series diverges to infinity when the complex series is not absolutely convergent.

The complementary case can be treated as well. If the coefficients are only non-zero for $k=2j+1$, then the partial sums are given by

$$S_{n}(\theta) = \sum_{j=0}^{n}a_{2j+1}e^{\mbox{\boldmath$... ...} \sum_{j=0}^{n}a_{2j+1}e^{\mbox{\boldmath$\imath$}2j\theta}.$$

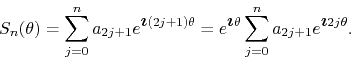
Using once again the variable $\theta'=2\theta$ and the coefficients $a'_{j}=a_{2j+1}$, we may write this as

$$S_{n}(\theta') = e^{\mbox{\boldmath$\imath$}\theta'/2} \sum_{k=0}^{n}a'_{k}e^{\mbox{\boldmath$\imath$}k\theta'},$$

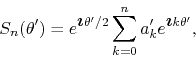
so that once more the problem can be reduced to the previous one, and so the result holds in this case as well. Just as in the previous case, there are two special points in this one, $\theta'=0$ and $\theta'=2\pi$, corresponding to $\theta=0$ and $\theta=\pi$. At these points the sine series converges to zero for the same reason as before, while at $\theta=0$ we have $\cos(k\theta)=1$ for all $k$, and at $\theta=\pi$ we have $\cos(k\theta)=-1$ for all terms of the series because $k$ is odd, so that the cosine series diverges to positive or negative infinity when the complex series is not absolutely convergent. This case includes the paradigmatic example of the square wave, that has a series of sines with this type of structure, and two points of discontinuity.

It is immediately apparent that we may further extend the results to series with coefficients having alternating signs, given for example by $(-1)^{k}$, so long as both the positive and negative coefficients approach zero monotonically. This type of series can be separated as the sum of two sub-series, either one of which is convergent by our theorem, and therefore they converge as well, possibly with the exception of a couple of special points in the case of the cosine series. In fact, this can be generalized to cases where the original series can be decomposed into a finite number of disjoint sub-series, each of which has coefficients that approach zero monotonically, but in order to do this we must first discuss series with non-zero terms only every so many terms, instead of every other term.

This type of extension can be generalized without difficulty to sparser series, with non-zero coefficients only every so many terms, so long as they come with a regular step. The extensions just discussed correspond to the case of step $2$, and in general the result holds as well for series with step $p$, which have then $p$ special points. Also, in this case there are $p$ alternatives for the position of the first element of the sequence of non-zero terms, which may lead to varying scenarios with regard to the convergence of the sine and cosine series at the special points. When there is no absolute convergence at least one of the two series, the sine series or the cosine series, will diverge at the special points. Any series which does converge will do so to a function which is discontinuous at these points. Except for these special points, any sparse series with a constant step and coefficients that approach zero monotonically for large values of $k$ is convergent in almost all the periodic interval.

The identification of the special points of a given series can always be accomplished, by the use of the algorithm that follows. The divergence of the complex series at these points is always caused by the alignment of all the vectors $v^{k}$ in the complex plane. This happens whenever the argument of the periodic functions returns to the same value from one element of the sequence of terms to the next, that is, when $k$ varies by the length one step of the series, $\Delta k=p$. Therefore the special points are determined by the condition

$$\begin{eqnarray*} \Delta k\theta & = & n\,2\pi \Rightarrow \\ \theta & = & \frac{n\,2\pi}{p}, \end{eqnarray*}$$

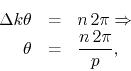
for some integer $n$. The values of $\theta$ at the special points are determined by the values of $n$ such that this angle falls within the periodic interval $[-\pi,\pi]$. One can verify that there are always $p$ such values of $n$. One can then determine whether the sine and cosine series converge or diverge by substituting these values in these periodic functions. The series can converge when there is no absolute convergence only if the periodic function is zero for all values of $k$. Otherwise the series diverges to infinity. By using this simple algorithm one can always determine the state of convergence of each series in each special point.

We may further extend our result to what we may call step-$\kappa$ monotonic series. These are series in which all the coefficients may be non-zero, but that can be separated into $\kappa$ sub-series, each one with a uniform step of size $\kappa$. These step-$\kappa$ monotonic series are those with coefficients which satisfy the condition

$$\lim_{k\to\infty}a_{k}=0,$$

and the condition that there exist an integer $\kappa$ such that

$$a_{k+\kappa}\leq a_{k},\,\forall k,$$

above a certain minimum value of $k$. Since the number of component sub-series is finite, so long as all $\kappa$ sub-series are convergent by the monotonicity criterion, it follows that their sum will necessarily converge as well. This establishes the convergence of the original series in all the domain except for a finite set of $\kappa$ special points, which are common to all the component sub-series, and for which we cannot conclude anything by this method.

Observe that we may have both positive and negative coefficients coexisting in such a series, so long as $a_{k}$ and $a_{k+\kappa}$ always have the same sign. The alternating-sign series discussed before, with coefficients with one sign for the even indices and the other sign for the odd indices, are simple examples of step-$2$ monotonic series.

A more general extension is simple to state, but is such that the series belonging to it are not so easy to identify. One may consider the set of all finite linear combinations of component series which have coefficients that approach zero monotonically. The component series may all have steps different from each other, and their coefficients may approach zero at different and arbitrary rates. So long as the number of series in the linear combination is finite, the resulting series is convergent, possibly with the exception of a finite set of special points. Note that in this case the resulting series may not have coefficients that approach zero monotonically at all.

At last, since the series $S(\theta)$ and $C(\theta)$ converge to the same point, so long as the coefficients $a_{k}$ tend to zero for $k\to\infty$, and since the series $C(\theta)$ converges typically much faster than $S(\theta)$, in any case in which the series $C(\theta)$ converges at all, even if does not do so absolutely, the series $S(\theta)$ must converge as well. Next we elaborate on the algorithmic significance of the relation between these two series.