Next: Extension of the Result Up: On the Convergence of Previous: Proof of a Simple
The same complex arithmetic used in the previous section can be employed
for the construction a rigorous and direct demonstration that the sequence
![]() is convergent. The argument is very similar to a demonstration of
the Dirichlet convergence test. In order to do this we show below that,
for
is convergent. The argument is very similar to a demonstration of
the Dirichlet convergence test. In order to do this we show below that,
for ![]() , the sequence
, the sequence ![]() is a Cauchy sequence within a closed
disc in the complex plane, which implies that it is convergent. The
demonstration is quite simple and short. We simply consider the partial
sums
is a Cauchy sequence within a closed
disc in the complex plane, which implies that it is convergent. The
demonstration is quite simple and short. We simply consider the partial
sums
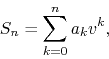
multiply by ![]() and manipulate the summation indices in order to
obtain, in a way similar to the manipulations done before,
and manipulate the summation indices in order to
obtain, in a way similar to the manipulations done before,
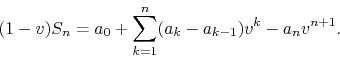
Taking now absolute values and using the triangular inequalities we get
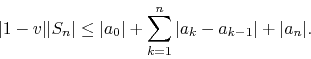
Assuming now that the sequence of coefficients ![]() decreases
monotonically to zero, we may write
decreases
monotonically to zero, we may write
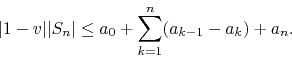
Once again almost all terms in the remaining sum cancel out in pairs, and we are left with
It follows that, so long as ![]() , we may write a finite upper bound
to the partial sum,
, we may write a finite upper bound
to the partial sum,
which does not depend on ![]() , and is therefore valid for all
, and is therefore valid for all ![]() . We
conclude therefore that the whole set of partial sums is contained within
a closed disc of radius
. We
conclude therefore that the whole set of partial sums is contained within
a closed disc of radius ![]() , centered at the origin, which is the
initial point of the sequence. As a consequence, given any two partial
sums
, centered at the origin, which is the
initial point of the sequence. As a consequence, given any two partial
sums ![]() and
and ![]() , the distance between them is less than
, the distance between them is less than ![]() ,
,
for any ![]() and any
and any ![]() . It is not difficult to repeat this argument for
a sum that starts at an arbitrary intermediate point
. It is not difficult to repeat this argument for
a sum that starts at an arbitrary intermediate point ![]() of the sequence,
and goes up to a point
of the sequence,
and goes up to a point ![]() . This is the difference of two partial sums
of the series,
. This is the difference of two partial sums
of the series,
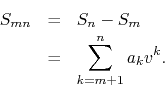
Repeating for ![]() the same manipulations executed before for
the same manipulations executed before for ![]() ,
we get this time
,
we get this time
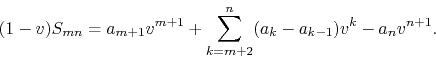
Taking now absolute values we get
In this way we see that, so long as ![]() , all the elements of the
sequence
, all the elements of the
sequence ![]() with
with ![]() are within a closed disc centered at
are within a closed disc centered at ![]() ,
with a finite radius
,
with a finite radius ![]() ,
,
which is independent of ![]() , so that this relation is valid for all
, so that this relation is valid for all ![]() .
It follows that any two elements
.
It follows that any two elements ![]() and
and ![]() of the sequence such
that
of the sequence such
that ![]() and
and ![]() are within this disc, and hence the distance between
them is bounded by the diameter of the disc,
are within this disc, and hence the distance between
them is bounded by the diameter of the disc,
This establishes the Cauchy-sequence structure of our sequence ![]() .
In order to complete the argument, let a real number
.
In order to complete the argument, let a real number ![]() be
given. We consider the infinite collection of positive real numbers
be
given. We consider the infinite collection of positive real numbers
all of which are finite so long as ![]() . Since we have by our
hypotheses that
. Since we have by our
hypotheses that ![]() when
when ![]() , it follows that there is
a value of
, it follows that there is
a value of ![]() such that
such that
If we consider this value of ![]() , then it follows that, for any
, then it follows that, for any ![]() and
any
and
any ![]() , it is true that
, it is true that
which establishes that there is a value of ![]() that satisfies the
criterion for a Cauchy sequence. Since
that satisfies the
criterion for a Cauchy sequence. Since ![]() is thus shown to be a
Cauchy sequence within a closed disc, which is a complete set, it follows
that it converges. As a consequence, so long as
is thus shown to be a
Cauchy sequence within a closed disc, which is a complete set, it follows
that it converges. As a consequence, so long as ![]() the Fourier
cosine and sine series that correspond to the sequence
the Fourier
cosine and sine series that correspond to the sequence ![]() are both
convergent. The same comments made before about the special case
are both
convergent. The same comments made before about the special case ![]() still apply, of course, so that the sine series converges everywhere,
while the cosine series converges at all points except
still apply, of course, so that the sine series converges everywhere,
while the cosine series converges at all points except ![]() .
.