Next: Rigorous Proof of the Up: On the Convergence of Previous: Geometrical Representation on the
Let us assume that the coefficients ![]() of
of ![]() are all
positive and that they constitute a sequence which decreases to zero
monotonically, that is, we assume the hypotheses
are all
positive and that they constitute a sequence which decreases to zero
monotonically, that is, we assume the hypotheses
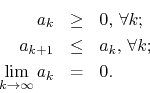
Note however that no statement at all is made about the rate in which
![]() approaches zero. This is enough to ensure that the series is
convergent for
approaches zero. This is enough to ensure that the series is
convergent for ![]() , as can be established by the use of the
Dirichlet convergence test. Nevertheless, we will give a proof based on
the geometrical representation of the series on the complex plane, because
it allows us to examine the behavior of the series in the case
, as can be established by the use of the
Dirichlet convergence test. Nevertheless, we will give a proof based on
the geometrical representation of the series on the complex plane, because
it allows us to examine the behavior of the series in the case ![]() and leads to an efficient summation technique in the convergent cases. We
will show that these simple hypotheses suffice to ensure the convergence
of the series
and leads to an efficient summation technique in the convergent cases. We
will show that these simple hypotheses suffice to ensure the convergence
of the series ![]() almost everywhere, in a sense which will be made
clear during the argument. The result we will obtain here can be easily
extended from this case to several others, but for definiteness let us
consider only this case for the moment.
almost everywhere, in a sense which will be made
clear during the argument. The result we will obtain here can be easily
extended from this case to several others, but for definiteness let us
consider only this case for the moment.
Interestingly, it is useful to analyze first a simple case that does not
quite satisfy these hypotheses, namely the case in which ![]() for all
values of
for all
values of ![]() . This case does not satisfy our hypotheses since this
sequence of coefficients fails to approach zero when
. This case does not satisfy our hypotheses since this
sequence of coefficients fails to approach zero when ![]() , which
implies that the series must diverge. From now on we will denote the
, which
implies that the series must diverge. From now on we will denote the ![]() basis element by
basis element by ![]() ,
,
so that in this simple case the partial sums of the series ![]() can
be written as sums of powers of
can
be written as sums of powers of ![]() ,
,
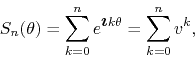
where ![]() is a unit vector making an angle of value
is a unit vector making an angle of value ![]() with the
real axis. In this simple case it is not difficult to verify, using the
geometry of the complex plane, that the partial sums of the vectors
with the
real axis. In this simple case it is not difficult to verify, using the
geometry of the complex plane, that the partial sums of the vectors
![]() run indefinitely around a circle, making infinite turns around it,
as illustrated in Figure 2. The series fails therefore
to converge, and oscillates indefinitely instead. There is, of course, an
exception in the case
run indefinitely around a circle, making infinite turns around it,
as illustrated in Figure 2. The series fails therefore
to converge, and oscillates indefinitely instead. There is, of course, an
exception in the case ![]() , since in this case all the vectors
, since in this case all the vectors
![]() are equal to one and therefore the series diverges linearly to
positive infinity along the real axis. For any other value of
are equal to one and therefore the series diverges linearly to
positive infinity along the real axis. For any other value of ![]() the
partial sums turn around a circle with a certain finite radius.
the
partial sums turn around a circle with a certain finite radius.
From the geometry shown in Figure 2 it is not difficult
to verify that the radius ![]() of the circle is given by
of the circle is given by
The position of the center of rotation ![]() is also easily verified to be
given by
is also easily verified to be
given by
so that regardless of the value of ![]() the center is over the
vertical line
the center is over the
vertical line ![]() of the complex plane
of the complex plane
![]() . However, it is
more interesting and useful to develop a different version of the formula
for the position of
. However, it is
more interesting and useful to develop a different version of the formula
for the position of ![]() , based solely on complex arithmetic, which
produces a simple result in terms of
, based solely on complex arithmetic, which
produces a simple result in terms of ![]() . We will do this in steps.
. We will do this in steps.
First, consider the first vector ![]() alone, and how to go from its
tip to the center
alone, and how to go from its
tip to the center ![]() . One can do this by going back to the middle of the
vector, and then proceeding perpendicularly to it by a length
. One can do this by going back to the middle of the
vector, and then proceeding perpendicularly to it by a length ![]() . The
first step is accomplished by subtracting
. The
first step is accomplished by subtracting ![]() . For the second step,
we consider the unit vector
. For the second step,
we consider the unit vector
![]() , which is perpendicular to
, which is perpendicular to
![]() , being rotated from it by
, being rotated from it by ![]() in the positive
(counterclockwise) direction. In order to go to the center, we must then
add
in the positive
(counterclockwise) direction. In order to go to the center, we must then
add
![]() , so that the complete path from the origin to
, so that the complete path from the origin to ![]() is
given arithmetically by
is
given arithmetically by
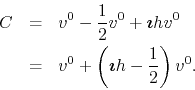
It is easy to verify that this is the same formula for ![]() given before.
Similarly, we can get to the center from the tip of the second vector
given before.
Similarly, we can get to the center from the tip of the second vector
![]() , and the complex arithmetic representing the complete path in this
case is
, and the complex arithmetic representing the complete path in this
case is
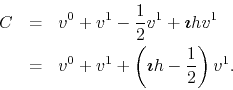
It is now easy to generalize this expression, representing arithmetically
the path from the origin to the center, through the tip of the ![]() -th
vector of the chain, by
-th
vector of the chain, by
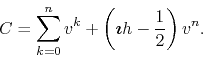
It is clear that, since the center of the circle is a fixed point in this
simple case, all these formulas, for any value of ![]() , produce the same
result, and that the complex number
, produce the same
result, and that the complex number ![]() above does not really depend on
above does not really depend on
![]() . The comparison of the first two formulas, for
. The comparison of the first two formulas, for ![]() and
and ![]() , allows
us to write the factor
, allows
us to write the factor
![]() in terms of
in terms of ![]() ,
,
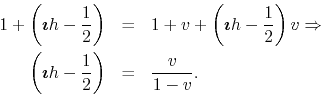
Therefore, the position of the center is given by any one of the family of formulas
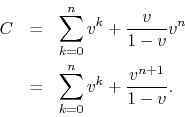
We see therefore that ![]() can be written in terms of the partial sums
can be written in terms of the partial sums
![]() of the
of the ![]() series,
series,
This is true even for the case ![]() , which gives us the simplest form for
, which gives us the simplest form for
![]() ,
,
We see here that, in the limit ![]() , for which
, for which ![]() , this
point diverges to infinity, and corresponds to a circle with infinite
radius that goes through the origin. This is the case in which the series
diverges to infinity along the real axis, while
, this
point diverges to infinity, and corresponds to a circle with infinite
radius that goes through the origin. This is the case in which the series
diverges to infinity along the real axis, while ![]() goes to infinity along
the line
goes to infinity along
the line ![]() . For any other value of
. For any other value of ![]() the center is at a
finite distance from the origin, and the series runs around it
indefinitely.
the center is at a
finite distance from the origin, and the series runs around it
indefinitely.
Let us now verify what happens when we generalize this analysis to the
case in which ![]() decreases monotonically to zero. We may limit the
discussion to the case in which
decreases monotonically to zero. We may limit the
discussion to the case in which ![]() without loss of generality,
since it is always possible to put
without loss of generality,
since it is always possible to put ![]() in evidence on the whole series
and rename the remaining coefficients accordingly. If we consider the new
sum and corresponding chain of vectors, each vector has the same direction
as before, but their lengths now decrease from
in evidence on the whole series
and rename the remaining coefficients accordingly. If we consider the new
sum and corresponding chain of vectors, each vector has the same direction
as before, but their lengths now decrease from ![]() . It is easy to
see that in this case the chain tends to spiral inwards within the
original circle, as illustrated in Figure 3. Besides,
the center of rotation is no longer fixed, but drifts from step to step in
the summation sequence.
. It is easy to
see that in this case the chain tends to spiral inwards within the
original circle, as illustrated in Figure 3. Besides,
the center of rotation is no longer fixed, but drifts from step to step in
the summation sequence.
One can see that, if the coefficients ![]() approach zero very slowly,
then the center also drifts very slowly, while the chain of partial sums
spirals around many times. On the other hand, if the coefficients
approach zero very slowly,
then the center also drifts very slowly, while the chain of partial sums
spirals around many times. On the other hand, if the coefficients ![]() approach zero very fast, then the center drifts faster, and the chain of
partial sums spirals around only a few times, if at all. The essential
element of the proof of convergence is the idea of following the drift of
the center, rather than the spiraling of the chain of partial sums.
approach zero very fast, then the center drifts faster, and the chain of
partial sums spirals around only a few times, if at all. The essential
element of the proof of convergence is the idea of following the drift of
the center, rather than the spiraling of the chain of partial sums.
We have therefore a sequence of points which we may call ``instantaneous
centers of rotation'',
![]() , that corresponds
to the sequence of partial sums
, that corresponds
to the sequence of partial sums
![]() . The same
arithmetic arguments we used before can be used in this case to give
. The same
arithmetic arguments we used before can be used in this case to give
![]() in terms of
in terms of ![]() . We now have the partial sums
. We now have the partial sums
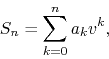
and the path to get to the center ![]() via the tip of the chain
via the tip of the chain ![]() is represented arithmetically by
is represented arithmetically by
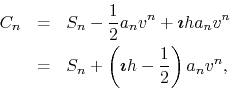
where ![]() is the same as before, leading to the expression, in terms of
is the same as before, leading to the expression, in terms of
![]() only,
only,
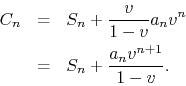
It is important to observe now that the distance from a partial sum to the
corresponding center, which is given by ![]() , is proportional
to
, is proportional
to ![]() ,
,
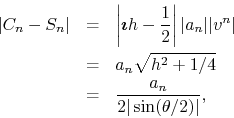
and therefore goes to zero when ![]() , so long as
, so long as ![]() is not
zero or a multiple of
is not
zero or a multiple of ![]() . Therefore, the partial sums approach the
drifting center in the
. Therefore, the partial sums approach the
drifting center in the ![]() limit, and hence the two sequences,
limit, and hence the two sequences,
![]() and
and ![]() , have the same limit.
, have the same limit.
We may now consider the series ![]() corresponding to the partial
sums
corresponding to the partial
sums ![]() , and the corresponding chain of complex vectors, in analogy
with what we did for the
, and the corresponding chain of complex vectors, in analogy
with what we did for the ![]() series. We will now show that, if the
coefficients
series. We will now show that, if the
coefficients ![]() satisfy our hypotheses, then this series is in fact
absolutely convergent, so long as
satisfy our hypotheses, then this series is in fact
absolutely convergent, so long as ![]() . From the relation between
. From the relation between
![]() and
and ![]() , multiplying by
, multiplying by ![]() , we get
, we get
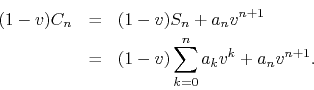
In order to write the resulting expression as a power series in ![]() , me
manipulate the sums and indices in order to get
, me
manipulate the sums and indices in order to get
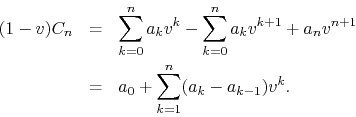
If we take absolute values and use the triangular inequalities, we get
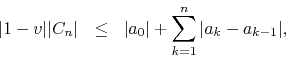
since ![]() has unit modulus. Since the coefficients
has unit modulus. Since the coefficients ![]() decrease
monotonically to zero, we may write this as
decrease
monotonically to zero, we may write this as
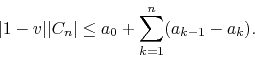
We now observe that in the remaining sum almost all terms cancel out in
pairs, except for one ![]() and one
and one ![]() , so that we have
, so that we have
If we now take the ![]() limit, by our hypotheses
limit, by our hypotheses ![]() vanishes,
and we get
vanishes,
and we get
Therefore, since ![]() is a given finite real number, the series
is a given finite real number, the series
![]() is absolutely convergent and, so long as
is absolutely convergent and, so long as ![]() , so is
the series
, so is
the series ![]() , for which we have
, for which we have
In either case the length of the chain associated to the series is finite,
thus characterizing a situation of absolute convergence. This establishes
the convergence of ![]() for the case
for the case ![]() , and since
, and since
![]() converges to
converges to ![]() , it also establishes the convergence of
, it also establishes the convergence of
![]() .
.
Before we give a more rigorous proof of this result, let us discuss it in
terms of the two separate real series, the one with the cosines and the
one with the sines. If ![]() , then it is clear that both series
converge. The single point
, then it is clear that both series
converge. The single point ![]() requires special consideration. In
this case we have
requires special consideration. In
this case we have ![]() , the radius of the circle becomes infinite, and
the complex series diverges to infinity along the real axis. This implies
that only its real part diverges, while its imaginary part is in fact
identically zero. Therefore, the conclusion is that the series of sines
always converges, while the series of cosines converges at all points
except one, the point
, the radius of the circle becomes infinite, and
the complex series diverges to infinity along the real axis. This implies
that only its real part diverges, while its imaginary part is in fact
identically zero. Therefore, the conclusion is that the series of sines
always converges, while the series of cosines converges at all points
except one, the point ![]() .
.
We may use the geometrical ideas presented here in order to understand the
origin of the discontinuity of the sine series at the special point
![]() . This discontinuity will appear when
. This discontinuity will appear when ![]() decreases slowly
with
decreases slowly
with ![]() , so that the series is not absolutely convergent, and the center
of rotation drifts very little from its initial position. For
, so that the series is not absolutely convergent, and the center
of rotation drifts very little from its initial position. For ![]() small and positive the center
small and positive the center ![]() will be in the upper half-plane, far
from the real axis, and the chain of vectors will curve slowly upwards,
away from the real axis, in order to eventually converge to that center.
However, if
will be in the upper half-plane, far
from the real axis, and the chain of vectors will curve slowly upwards,
away from the real axis, in order to eventually converge to that center.
However, if ![]() is small and negative, then the center
is small and negative, then the center ![]() will be in
the lower half-plane, again far from the real axis, and the chain of
vectors will curve slowly downwards. We see therefore that there will be a
discontinuity, since an infinitesimal variation that flips the sign of
will be in
the lower half-plane, again far from the real axis, and the chain of
vectors will curve slowly downwards. We see therefore that there will be a
discontinuity, since an infinitesimal variation that flips the sign of
![]() will result in a large jump in the imaginary part of the point of
convergence, from strictly positive to strictly negative values.
will result in a large jump in the imaginary part of the point of
convergence, from strictly positive to strictly negative values.