Geometrical Representation on the Complex Plane

Since the complex functions $\exp(\mbox{\boldmath$\imath$}k\theta)$ can be represented as unit vectors in the complex plane $z=x+\mbox{\boldmath$\imath$}y$, the partial sums of the series $S(\theta)$, which are given by

$$S_{n}(\theta) = \sum_{k=0}^{n}a_{k}e^{\mbox{\boldmath$\imath$}k\theta},$$

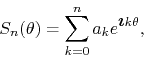
can be represented very simply and elegantly on the complex plane, because the direction of each vector $a_{k}\exp(\mbox{\boldmath$\imath$}k\theta)$ is given solely by the unit-length basis element $\exp(\mbox{\boldmath$\imath$}k\theta)$, while its length is given solely by $\vert a_{k}\vert$. The partial sum $S_{n}(\theta)$ is a sum of $n$ such vectors, which can be represented by drawing the vectors consecutively on the plane, starting from the origin, forming in this way a chain of complex vectors, formed by segments connected end-to-end at certain points, as illustrated in Figure 1. The complete series is represented by an infinite chain of such vectors. The set of vertex points along this infinite chain is identical to the set of partial sums of the series. Therefore, the convergence of the series is translated in this geometrical representation onto the fact that this sequence of points has a limit, and approaches some fixed point of the complex plane.

Figure: A generic chain of vectors $a_{k}\exp(\mbox{\boldmath$\imath$}k\theta)$ on the complex plane $z=x+\mbox{\boldmath$\imath$}y$.

It now becomes immediately clear that the absolute convergence of the series is equivalent to the complete chain of vectors having a finite total length. One can see this because the series is absolutely convergent if and only if the sum of the moduli of the coefficients is finite, since the basis elements have unit moduli. In short, absolute converge means that the sum

$$\bar{S}_{n} = \sum_{k=0}^{n}\vert a_{k}\vert$$

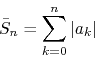
converges to a finite limit when $n\to\infty$. Since the modulus of each coefficient gives the length of one of the vectors in the chain, this sum is the total length of the chain. If the series is absolutely convergent, then this sum is finite and so is the length of the chain. Likewise, if the chain has a finite length then this sum is finite and the series is absolutely convergent. If the series $S(\theta)$ is absolutely convergent, then it is also convergent, and hence both the cosine and the sine series, its real and imaginary parts, are convergent.

This relation is intuitively clear, since it is obvious that, if the chain has a finite total length, then it cannot extend to infinity, nor can it oscillate indefinitely between two points. It must extend a finite amount and hence stop at some point of the complex plane, which is its point of convergence. In this paper we will concern ourselves mostly with the case in which the series is convergent, but not absolutely convergent. In this case the chain has infinite total length, and then the series may fail to converge by extending to infinity or by oscillating indefinitely.

It is clear that the point $\theta=0$ presents a particular convergence behavior, since for this value all the basis elements become equal to one, and hence the chain extends only over the real axis of the complex plane. It the series is not absolutely convergent, the chain has infinite length, and may easily extend to infinity. This is not certain only due to the possibility of successive exchanges of the signs of $a_{k}$, since the cancellations thus introduced may make the series converge, with the chain folding repeatedly over itself.

It is important to recall at this point that, if the series is not absolutely convergent, then the order in which the sum is executed may affect the final result. In this case, any statement of convergence must state the order in which the summation is meant to proceed. When we draw the chain in the complex plane, we are automatically adopting a particular order, the natural order of the sequence, with increasing values of the index $k$. This order will always be assumed here, unless otherwise noted.

Next, we will prove a theorem concerning the convergence of the complex series $S(\theta)$, that involves a criterion based on the behavior of the real coefficients $a_{k}$.