Introduction

The work presented here resulted as a by-product of the development of a course of lectures on mathematical physics. In this course the Fourier series is used in its usual role for the solution of boundary value problems in partial differential equations. The convergence problem appears naturally in such a context, but leads to a point of view slightly different from that of the usual treatment. The usual criteria for convergence are based on the analytical properties of the function to which the series is associated. The known convergence theorems give sufficient conditions for the convergence of the series associated to a function. So far as the author knows, the formulation of a necessary and sufficient condition is still an open problem.

However, in applications to partial differential equations, what one has by the end of the day is the set of Fourier coefficients rather than the values of the function, so it is important to have convergence criteria based solely on the behavior of these coefficients, rather than on the analytical properties of the limiting function. This is the type of convergence criteria discussed in this paper. The criteria of this type for the absolute and uniform convergence of the series are well-known, and will be reviewed here in the context of a geometrical representation on the complex plane. We then focus on the criteria for the case in which there is simple point-wise convergence but not absolute or uniform convergence.

Let us review then some of the basic concepts, in order to establish context and notation. Let $f(\theta)$ be a real-valued function of the real variable $\theta$, with domain in the interval $[-\pi,\pi]$, on which we impose periodic boundary conditions, that is, with $-\pi$ and $\pi$ identified as the same point. No constraints other than that it be bounded and integrable are imposed on the function $f(\theta)$. The Fourier series associated with $f(\theta)$ is given by

$$S(\theta) = \frac{\alpha_{0}}{2} + \lim_{n\to\infty} \... ... \alpha_{k}\cos(k\theta) + \beta_{k}\sin(k\theta) \right],$$

where the coefficients are given by

$$\begin{eqnarray*} \alpha_{k} & = & \frac{1}{\pi}\int_{-\pi}^{\pi}d\theta\, f... ...\frac{1}{\pi}\int_{-\pi}^{\pi}d\theta\, f(\theta)\sin(k\theta). \end{eqnarray*}$$

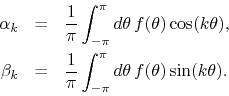
We will indicate the series symbolically as

$$S(\theta) = \frac{\alpha_{0}}{2} + \sum_{k=1}^{\infty} ... ... \alpha_{k}\cos(k\theta) + \beta_{k}\sin(k\theta) \right],$$

which is a notation indicating that there is an implicit limiting procedure involved. The set of functions

$$% \renewedcommand{arraystretch}{2.1} \begin{array}{lcl} ... ...in(k\theta), & \mbox{ for } & k=1,\ldots,\infty, \end{array}$$

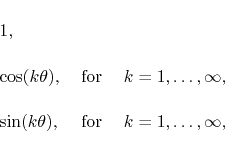
is complete, which means that it can be used as a basis to represent all sufficiently well-behaved bounded periodic functions on the interval $[-\pi,\pi]$. This means that, if the series $S(\theta)$ converges at all, then it converges to the function $f(\theta)$, with the possible exception of a set of isolated points within the interval, which constitutes a zero-measure set. At points where $f(\theta)$ is continuous the series, if convergent, converges to the function. At points where it is discontinuous, the series, if convergent, converges to the average of the two lateral limits of $f(\theta)$ at that point, if these limits exist.

All these are well-known facts concerning the Fourier series [1]. In most of this paper we will not be concerned with the nature of the limit of the series, but only with the fact of its convergence. Since the set of $\cos(k\theta)$ functions and the set of $\sin(k\theta)$ functions are independent sets, the complete series can be convergent only if the separate series of $\cos(k\theta)$ functions and of $\sin(k\theta)$ functions converge independently. One can see this most simply by decomposing $f(\theta)$ in its even and odd parts,

$$f(\theta) = \frac{f(\theta)+f(-\theta)}{2} + \frac{f(\theta)-f(-\theta)}{2} = f_{e}(\theta)+f_{\theta}(\theta),$$

a decomposition that can always be made, regardless of any properties of the function. The same decomposition can be used for $S(\theta)=S_{e}(\theta)+S_{o}(\theta)$, and since the trigonometric functions involved have well-defined parities, this decomposition leads to

$$\begin{eqnarray*} S_{e}(\theta) & = & \frac{\alpha_{0}}{2} + \sum_{k=1}^{\i... ...{o}(\theta) & = & \sum_{k=1}^{\infty} \beta_{k}\sin(k\theta), \end{eqnarray*}$$

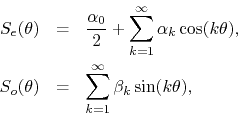
where the coefficients may be written in terms of the parts of the function $f(\theta)$ with the corresponding parities,

$$\begin{eqnarray*} \alpha_{k} & = & \frac{1}{\pi}\int_{-\pi}^{\pi}d\theta\, f... ...c{1}{\pi}\int_{-\pi}^{\pi}d\theta\, f_{o}(\theta)\sin(k\theta). \end{eqnarray*}$$

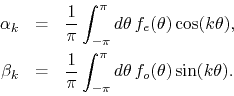
We see therefore that the even and odd parts do not mix, and if one is to determine whether or not the Fourier series of a given function converges, one must do so independently for the even and odd parts of that function. In one case the series involved is purely a cosine series, and in the other purely a sine series. Each one of these series can be expressed as the real or imaginary part of a corresponding complex series, still with real coefficients,

$$\begin{eqnarray*} \frac{\alpha_{0}}{2} + \sum_{k=1}^{\infty} \alpha_{k}\cos(... ...}^{\infty}\beta_{k}e^{\mbox{\boldmath$\imath$}k\theta} \right]. \end{eqnarray*}$$

If we use the generic name $a_{k}$ for the real coefficients $\alpha_{k}$ or $\beta_{k}$, as the case may be, we may, in a simpler way and with complete equivalence with the original problem, examine the convergence of the complex series with real coefficients $a_{k}$ given by

$$S(\theta) = \sum_{k=0}^{\infty}a_{k}e^{\mbox{\boldmath$\imath$}k\theta}.$$

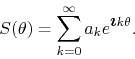
The Fourier basis can therefore be represented, in its complex form, by the set of functions

$$e^{\mbox{\boldmath$\imath$}k\theta},\mbox{\ \ \ for\ \ \ }k=0,\ldots,\infty.$$

It should be noted that this is not the complex version of the Fourier series, which would in general involve complex coefficients. It is simply a construction that allows us to study, in a simple and convenient way, the convergence of both the cosine series and the sine series, with the same arbitrary set of real coefficients $a_{k}$, in terms of the properties of these coefficients.