The First Slow-Converging Case

The function we will adopt as our original function, which is an odd function of $\theta$, is shown in Figure 7. It is given by the DP Fourier series

$$f_{\rm s}(\theta) = \frac{2}{\pi} \sum_{k=1}^{\infty} \frac{1}{\sqrt{k}}\, \sin(k\theta),$$

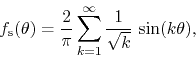
and the corresponding FC function is then given by the DP Fourier series

$$f_{\rm c}(\theta) = \frac{2}{\pi} \sum_{k=1}^{\infty} \frac{1}{\sqrt{k}}\, \cos(k\theta).$$

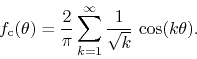
These two series are convergent almost everywhere, but not absolutely or uniformly convergent. There is a single special point at $\theta=0$, where we have for the original function $f_{\rm s}(0)=0$. However, the function is not continuous at this point, and its lateral limits to it diverge to $\pm\infty$. In fact, at this point both the original function and the corresponding FC function diverge logarithmically. The representation of the original function in terms of the first-order center series is given by

$$f_{\rm s}(\theta) = \frac{1}{\pi\sin(\theta/2)} \left\{ ... ...}{\sqrt{k}(k+1)+k\sqrt{k+1}}\, \cos[(k+1/2)\theta] \right\},$$

for $\theta\neq 0$, and the representation of the corresponding FC function in terms of the first-order center series is given by

$$f_{\rm c}(\theta) = \frac{1}{\pi\sin(\theta/2)} \left\{ ... ...}{\sqrt{k}(k+1)+k\sqrt{k+1}}\, \sin[(k+1/2)\theta] \right\},$$

for $\theta\neq 0$. These two series are absolutely and uniformly convergent. The representation of the original function in terms of the second-order center series is given by

$$\begin{eqnarray*} f_{\rm s}(\theta) & = & \frac{1}{4\pi\sin^{2}(\theta/2)} \... ... {\sqrt{k}\sqrt{k+1}\sqrt{k+2}}\, \sin[(k+1)\theta] \right\}, \end{eqnarray*}$$

for $\theta\neq 0$, and the representation of the corresponding FC function in terms of the second-order center series is given by

$$\begin{eqnarray*} f_{\rm c}(\theta) & = & \frac{1}{4\pi\sin^{2}(\theta/2)} \... ... {\sqrt{k}\sqrt{k+1}\sqrt{k+2}}\, \cos[(k+1)\theta] \right\}, \end{eqnarray*}$$

for $\theta\neq 0$. These two series are absolutely and uniformly convergent. The derivation of the center series can be found in Section A.7 of Appendix A, and the results of the tests are shown in the tables in Subsections B.13 and B.14 of Appendix B.

Figure 8: Second slow-converging case: the original function (solid line) and its conjugate function (dashed line) plotted within the periodic interval $[-\pi ,\pi ]$. The dotted lines mark the special point.