Next: The First Slow-Converging Case Up: Tests of Center Series Previous: The Shifted Square Wave
Consider the Fourier series of a unit-amplitude periodic function built
with segments of quadratic functions, joined together so that the
resulting function is continuous and differentiable, in such a way that
the result is an odd function of ![]() , as shown in
Figure 6. The original function is given by the DP Fourier
series
, as shown in
Figure 6. The original function is given by the DP Fourier
series
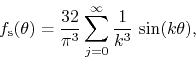
where ![]() , and the corresponding FC function is given by the DP
Fourier series
, and the corresponding FC function is given by the DP
Fourier series
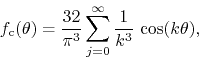
 |
where ![]() . These two series are absolutely and uniformly convergent.
There are two special points at
. These two series are absolutely and uniformly convergent.
There are two special points at ![]() and at
and at ![]() , where
we have for the original function
, where
we have for the original function
![]() and
and
![]() . At these points both the original function and the
corresponding FC function have singularities on their second
derivatives. The representation of the original function in terms of the
first-order center series is given by
. At these points both the original function and the
corresponding FC function have singularities on their second
derivatives. The representation of the original function in terms of the
first-order center series is given by
![\begin{displaymath}
f_{\rm s}(\theta)
=
\frac{16}{\pi^{3}\sin(\theta)}
\left...
...rac{6k(k+2)+8}{k^{3}(k+2)^{3}}\,
\cos[(k+1)\theta]
\right\},
\end{displaymath}](img80.png)
where ![]() , for
, for ![]() and
and
![]() , and the
representation of the corresponding FC function in terms of the
first-order center series is given by
, and the
representation of the corresponding FC function in terms of the
first-order center series is given by
![\begin{displaymath}
f_{\rm c}(\theta)
=
\frac{16}{\pi^{3}\sin(\theta)}
\left...
...rac{6k(k+2)+8}{k^{3}(k+2)^{3}}\,
\sin[(k+1)\theta]
\right\},
\end{displaymath}](img81.png)
where ![]() , for
, for ![]() and
and
![]() . These two
series are absolutely and uniformly convergent. The derivation of the
center series can be found in Section A.6 of
Appendix A, and the results of the tests are shown in
the tables in Subsections B.11 and B.12 of
Appendix B.
. These two
series are absolutely and uniformly convergent. The derivation of the
center series can be found in Section A.6 of
Appendix A, and the results of the tests are shown in
the tables in Subsections B.11 and B.12 of
Appendix B.