Next: First-Order Center Series Up: Derivations of Center Series Previous: Second-Order Center Series
Consider a continuous and differentiable periodic function built with segments of quadratic functions, given by the sine series
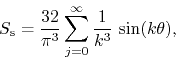
where ![]() . The corresponding FC series is then
. The corresponding FC series is then
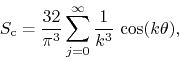
where ![]() . Note that due to the factors of
. Note that due to the factors of ![]() these series are
already absolutely and uniformly convergent. The complex power series
these series are
already absolutely and uniformly convergent. The complex power series
![]() is given by
is given by
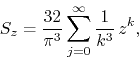
where ![]() , of which the two DP Fourier series above are the real and
imaginary parts on the unit circle.
, of which the two DP Fourier series above are the real and
imaginary parts on the unit circle.