Next: Convergence and Singularities Up: Fourier Theory on the Previous: Absolute and Uniform Convergence
Let us establish a general classification of the singularities of inner analytic functions on the unit circle. While it is possible that the scheme of classification that we describe here may have its uses in more general settings, for definiteness we consider here only the case of inner analytic functions that have one or more singularities on the unit circle. We also limit our attention to only those singular points, and ignore any singularities that may exist strictly outside the closed unit disk. In order to do this we must first establish some preliminary facts.
To start with, let us show that the operation of logarithmic
differentiation stays within the set of inner analytic functions. Let us
recall that, if ![]() is an inner analytic function, then it has the
properties that it is analytic on the open unit disk, that it is the
analytic continuation of a real function on the real interval
is an inner analytic function, then it has the
properties that it is analytic on the open unit disk, that it is the
analytic continuation of a real function on the real interval ![]() ,
and that
,
and that ![]() . These last two are consequences of the fact that its
Taylor series has the form
. These last two are consequences of the fact that its
Taylor series has the form
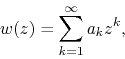
with real ![]() . We define the logarithmic derivative of
. We define the logarithmic derivative of ![]() as
as
which also establishes our notation for it. We might also write the first
logarithmic derivative as
![]() . Let us show that the
logarithmic derivative of an inner analytic function is another inner
analytic function. First, since the derivative of an analytic function is
analytic in exactly the same domain as that function, and since the
identity function
. Let us show that the
logarithmic derivative of an inner analytic function is another inner
analytic function. First, since the derivative of an analytic function is
analytic in exactly the same domain as that function, and since the
identity function ![]() is analytic in the whole complex plane, it follows
that if
is analytic in the whole complex plane, it follows
that if ![]() is analytic on the open unit disk, then so is
is analytic on the open unit disk, then so is
![]() . Second, if we calculate
. Second, if we calculate
![]() using the series
representation of
using the series
representation of ![]() , which converges in the open unit disk, since
, which converges in the open unit disk, since
![]() is analytic there, we get
is analytic there, we get
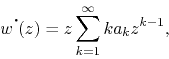
since a convergent power series can always be differentiated term-by-term.
It follows that, if the coefficients ![]() are real, then so are the new
coefficients
are real, then so are the new
coefficients ![]() , so that the coefficients of the Taylor series of
, so that the coefficients of the Taylor series of
![]() are real, and hence it too is the analytic continuation of
a real function on the real interval
are real, and hence it too is the analytic continuation of
a real function on the real interval ![]() . Lastly, due to the extra
factor of
. Lastly, due to the extra
factor of ![]() we have that
we have that
![]() . Hence, the logarithmic
derivative
. Hence, the logarithmic
derivative
![]() is an inner analytic function.
is an inner analytic function.
Next, let us define the concept of logarithmic integration. This is the
inverse operation to logarithmic differentiation, with the understanding
that we always choose the value zero for the integration constant. The
logarithmic primitive of ![]() may be defined as
may be defined as
Let us now show that the operation of logarithmic integration also stays
within the set of inner analytic functions. Note that since ![]() the
integrand is in fact analytic on the open unit disk, if we define it at
the
integrand is in fact analytic on the open unit disk, if we define it at
![]() by continuity, and therefore the path of integration from
by continuity, and therefore the path of integration from ![]() to
to ![]() is irrelevant, so long as it is contained within that disk. It is easier
to see this using the series representation of
is irrelevant, so long as it is contained within that disk. It is easier
to see this using the series representation of ![]() , which converges in
the open unit disk, since
, which converges in
the open unit disk, since ![]() is analytic there,
is analytic there,
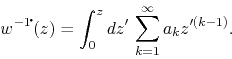
It is clear now that the integrand is a power series which converges
within the open unit disk, and thus converges to an analytic function
there. Since the primitive of an analytic function is analytic in exactly
the same domain as that function, it follows that the logarithmic
primitive
![]() is analytic on the open unit disk. If we now
execute the integration using the series representation, we get
is analytic on the open unit disk. If we now
execute the integration using the series representation, we get
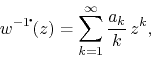
since a convergent power series can always be integrated term-by-term.
Since the coefficients ![]() are real, so are the new coefficients
are real, so are the new coefficients
![]() , and therefore
, and therefore
![]() is the analytic continuation
of a real function on the real interval
is the analytic continuation
of a real function on the real interval ![]() . Besides, one can see
explicitly that
. Besides, one can see
explicitly that
![]() . Therefore,
. Therefore,
![]() is an
inner analytic function. It is now easy to see also that the logarithmic
derivative of this primitive gives us back
is an
inner analytic function. It is now easy to see also that the logarithmic
derivative of this primitive gives us back ![]() .
.
Finally, let us show that the derivative of ![]() with respect to
with respect to
![]() is given by the logarithmic derivative of
is given by the logarithmic derivative of ![]() . Since we have
that
. Since we have
that
![]() , we may at once write that
, we may at once write that
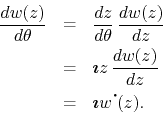
In the limit ![]() , where and when that limit exists, the derivative
of
, where and when that limit exists, the derivative
of ![]() with respect to
with respect to ![]() becomes the derivatives of the limiting
functions
becomes the derivatives of the limiting
functions
![]() and
and
![]() of the FC pair of DP
Fourier series. The factor of
of the FC pair of DP
Fourier series. The factor of
![]() effects the interchange of real and
imaginary parts, and the change of sign, that are consequences of the
differentiation of the trigonometric functions.
effects the interchange of real and
imaginary parts, and the change of sign, that are consequences of the
differentiation of the trigonometric functions.
We see therefore that, given an inner-analytic function and its set of
singularities on the unit circle, as well as the corresponding FC pair of
DP Fourier series, we may at once define a whole infinite chain of
inner-analytic functions and corresponding DP Fourier series, running by
differentiation to one side and by integration to the other, indefinitely
in both directions. We will name this an integral-differential
chain. We are now ready to give the complete formal definition of the
proposed classification of the singularities of inner analytic functions
![]() on the unit circle. Let
on the unit circle. Let ![]() be a point on the unit circle. We
start with the very basic classification which was already mentioned.
be a point on the unit circle. We
start with the very basic classification which was already mentioned.
Next we establish a gradation of the concepts of hardness and softness of
the singularities of ![]() . To each singular point
. To each singular point ![]() we attach an
integer giving either its degree of hardness or its degree of
softness. In order to do this the following definitions are adopted.
we attach an
integer giving either its degree of hardness or its degree of
softness. In order to do this the following definitions are adopted.
Finally, the following rules are adopted regarding the superposition of several singularities as the same point, brought about by the addition of functions.
It is not difficult to see that this classification spans all existing
possibilities in so far as the possible types of singularity go. First,
given a point of singularity, either the limit of the function to that
point from within the open unit disk exists or it does not. There is no
third alternative, and therefore every singularity is either soft or
hard. Second, given a soft singularity, either it becomes hard after a
certain finite number of logarithmic differentiations of ![]() , or it
does not. Similarly, given a hard singularity, either it becomes soft
after a certain finite number of logarithmic integrations of
, or it
does not. Similarly, given a hard singularity, either it becomes soft
after a certain finite number of logarithmic integrations of ![]() , or it
does not. In either case there is no third alternative. If the soft or
hard character never changes, then we classify the singularity as
infinitely soft or infinitely hard, as the case may be. Otherwise, we
assign to it a degree of softness or hardness by counting the number
, or it
does not. In either case there is no third alternative. If the soft or
hard character never changes, then we classify the singularity as
infinitely soft or infinitely hard, as the case may be. Otherwise, we
assign to it a degree of softness or hardness by counting the number ![]() of logarithmic differentiations or logarithmic integrations required to
effect its change of character, and assigning to it the number
of logarithmic differentiations or logarithmic integrations required to
effect its change of character, and assigning to it the number ![]() as
the degree of softness or hardness, as the case may be.
as
the degree of softness or hardness, as the case may be.
We now recall that there is a set of hard singularities which is already
classified, by means of the concept of the Laurent expansion around an
isolated singular point. If a singularity is isolated in two ways, first
in the sense that there is an open neighborhood around it that contains no
other singularities, and second that it is possible to integrate along a
closed curve around it which is closed in the sense that it does not pass
to another leaf of a Riemann surface when it goes around the point, then
one may write a convergent Laurent expansion for the function around that
point. This leads to the concepts of poles of finite orders and of
essential singularities. In particular, it implies that any analytic
function that has a pole of finite order at the point ![]() can be
written around that point as the sum of a function which is analytic at
that point and a finite linear combination of the singularities
can be
written around that point as the sum of a function which is analytic at
that point and a finite linear combination of the singularities
for
![]() , where
, where ![]() is the order of the pole.
We can use this set of singularities to illustrate our classification. For
example, if we have an inner analytic function
is the order of the pole.
We can use this set of singularities to illustrate our classification. For
example, if we have an inner analytic function ![]() with a simple pole
with a simple pole
![]() for
for ![]() on the unit circle, which is a hard singularity
with degree of hardness
on the unit circle, which is a hard singularity
with degree of hardness ![]() , then the logarithmic derivative of
, then the logarithmic derivative of ![]() has
a double pole
has
a double pole
![]() at that point, an even harder singularity,
of degree of hardness
at that point, an even harder singularity,
of degree of hardness ![]() . Further logarithmic differentiations of
. Further logarithmic differentiations of ![]() produce progressively harder singularities
produce progressively harder singularities
![]() , where
, where ![]() is
the degree of hardness of the singularity. We see therefore that multiple
poles fit easily and comfortably into the classification scheme. We may
now proceed to examine this chain of singularities in the other direction,
using logarithmic integration in order to do this.
is
the degree of hardness of the singularity. We see therefore that multiple
poles fit easily and comfortably into the classification scheme. We may
now proceed to examine this chain of singularities in the other direction,
using logarithmic integration in order to do this.
The logarithmic primitive of the function ![]() mentioned above has a
logarithmic singularity
mentioned above has a
logarithmic singularity ![]() at that point, which is the weakest
type of hard singularity in this type of integral-differential chain.
Another logarithmic integration produces a soft singularity such as
at that point, which is the weakest
type of hard singularity in this type of integral-differential chain.
Another logarithmic integration produces a soft singularity such as
![]() , which displays no divergence to infinity. This
establishes therefore that
, which displays no divergence to infinity. This
establishes therefore that ![]() is a borderline hard
singularity, with degree of hardness
is a borderline hard
singularity, with degree of hardness ![]() . If we now proceed to
logarithmically differentiate the resulting function, we get back the hard
singularity
. If we now proceed to
logarithmically differentiate the resulting function, we get back the hard
singularity ![]() . This establishes therefore that
. This establishes therefore that
![]() is a borderline soft singularity, with degree of
softness
is a borderline soft singularity, with degree of
softness ![]() . This illustrates the transitions between hard and soft
singularities, and also justifies our attribution of degrees of hardness
to the multiple poles, as we did above. Further logarithmic integrations
produce progressively softer singularities such as
. This illustrates the transitions between hard and soft
singularities, and also justifies our attribution of degrees of hardness
to the multiple poles, as we did above. Further logarithmic integrations
produce progressively softer singularities such as
![]() , and so on, were we consider only the hardest
or least soft singularity resulting from each operation and ignore regular
terms, leading to the general expression
, and so on, were we consider only the hardest
or least soft singularity resulting from each operation and ignore regular
terms, leading to the general expression
where ![]() is the degree of softness. This completes the examination of the
singularities of this particular type of integral-differential chain. Note
that these soft singularities are isolated in the sense that there is an
open neighborhood around each one of them that contains no other
singularities, but not in the sense that one can integrate in closed
curves around them. This is so because the domains of these functions are
in fact Riemann surfaces with infinitely many leaves, and a curve which is
closed in the complex plane is not really closed in the domain of the
function.
is the degree of softness. This completes the examination of the
singularities of this particular type of integral-differential chain. Note
that these soft singularities are isolated in the sense that there is an
open neighborhood around each one of them that contains no other
singularities, but not in the sense that one can integrate in closed
curves around them. This is so because the domains of these functions are
in fact Riemann surfaces with infinitely many leaves, and a curve which is
closed in the complex plane is not really closed in the domain of the
function.
Although this chain of singularities exhausts the possibilities so far as one is limited to integral-differential chains containing isolated hard singularities of single-valued functions, there are many other possible chains of singularities, if one starts with hard singularities having non-trivial Riemann surfaces, for example such as
for ![]() . One might consider also the more general form
. One might consider also the more general form
for the singularities, where ![]() and
and ![]() in any integer, positive or
negative. This generates quite a large set of possible types of
singularity, both soft and hard.
in any integer, positive or
negative. This generates quite a large set of possible types of
singularity, both soft and hard.
To complete the picture in our exemplification, a simple and widely known
example of an infinitely hard singularity is an essential singularity such
as
![]() . On the other hand, an infinitely soft singularity
is not such a familiar object. One interesting example will be discussed
in Section A.2 of Appendix A.
. On the other hand, an infinitely soft singularity
is not such a familiar object. One interesting example will be discussed
in Section A.2 of Appendix A.
It is important to note that almost all convergent DP Fourier series will
be related to inner analytic functions either with only soft singularities
on the unit circle or with at most borderline hard singularities, which
will therefore all have non-trivial Riemann surfaces as their domains.
Since in our analysis here we are bound within the unit disk, and will at
most consider limits to the unit circle from within that disk, this is not
of much concern to us, because in this case we never go around one of
these singularities in order to change from one leaf of the Riemann
surface to another. The value of the function ![]() within the unit disk
is defined by its value a the origin, and this determines the leaf of each
Riemann surface which is to be used within the disk. We must always
consider that the branching lines of all such branching points at the unit
circle extend outward from the unit circle, towards infinity.
within the unit disk
is defined by its value a the origin, and this determines the leaf of each
Riemann surface which is to be used within the disk. We must always
consider that the branching lines of all such branching points at the unit
circle extend outward from the unit circle, towards infinity.