Next: Appendix: Examples of Center Up: Appendix: Technical Proofs Previous: Evaluations of Convergence
Consider the following power series, which has coefficients that converge monotonically to zero from positive values,
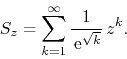
If we apply the ratio test to it, we get
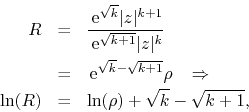
where ![]() . In the large-
. In the large-![]() limit we have
limit we have
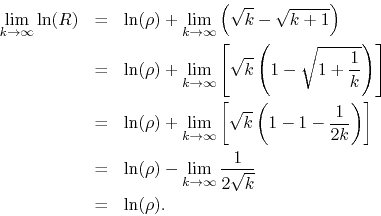
It follows that in the limit we have ![]() and therefore the conditions
of the test are satisfied if and only if
and therefore the conditions
of the test are satisfied if and only if ![]() . This establishes the
open unit disk as the maximum disk of convergence of the series. Within
this disk the series converges to an inner analytic function
. This establishes the
open unit disk as the maximum disk of convergence of the series. Within
this disk the series converges to an inner analytic function ![]() , and
we may write
, and
we may write
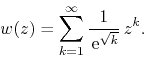
Since the maximum disk of convergence of the series is the open unit disk,
this function must have at least one singularity on the unit circle. Note
that since the series is monotonic with step ![]() , we already know that
, we already know that
![]() has a single dominant singularity on that circle, located at
has a single dominant singularity on that circle, located at ![]() .
Consider now the logarithmic derivatives of this function. Using the
series we have within the open unit disk, for the
.
Consider now the logarithmic derivatives of this function. Using the
series we have within the open unit disk, for the ![]() logarithmic
derivative of
logarithmic
derivative of ![]() ,
,
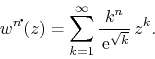
This notation includes the original series as the case ![]() . All these
series converge on the open unit disk, of course. Let us now consider the
corresponding series of absolute values, for
. All these
series converge on the open unit disk, of course. Let us now consider the
corresponding series of absolute values, for ![]() ,
,
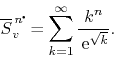
The terms of this sum can be bounded, for ![]() and some minimum value
and some minimum value
![]() of
of ![]() , by the function
, by the function ![]() , since we have that it is always
possible to find a value
, since we have that it is always
possible to find a value ![]() of a variable
of a variable ![]() such that for
such that for
![]() we have
we have
since the exponential goes to zero faster than any inverse power. Making
![]() and therefore
and therefore ![]() we have
we have
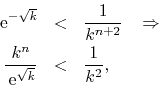
thus proving the assertion. This implies that all these series are
absolutely and uniformly convergent over the whole unit circle, to
continuous functions. Therefore, all these series must have a soft
singularity on the unit circle, at ![]() . This is one example in which we
may differentiate as many times as we will, without the singularity ever
becoming hard. Therefore, that singularity is necessarily an infinitely
soft one.
. This is one example in which we
may differentiate as many times as we will, without the singularity ever
becoming hard. Therefore, that singularity is necessarily an infinitely
soft one.
Note that in this case the DP Fourier series on the unit circle converge
to ![]() functions, although there are singularities on that
circle. Although these real functions are
functions, although there are singularities on that
circle. Although these real functions are ![]() , in the real sense
of this concept, the complex function
, in the real sense
of this concept, the complex function ![]() cannot be
cannot be ![]() on the
unit circle, in the complex sense of the concept. One may ask how can a
restriction of the complex function
on the
unit circle, in the complex sense of the concept. One may ask how can a
restriction of the complex function ![]() , which is
, which is ![]() in the
whole interior of the unit disk, be
in the
whole interior of the unit disk, be ![]() at the boundary of the
disk while
at the boundary of the
disk while ![]() itself is not.
itself is not.
The answer is that the ![]() condition in the real sense is a
weaker condition than the
condition in the real sense is a
weaker condition than the ![]() condition in the complex sense.
While in the case of the real functions on the unit circle only the
derivatives with respect to
condition in the complex sense.
While in the case of the real functions on the unit circle only the
derivatives with respect to ![]() must exist, in the case of the
complex function the derivatives in the perpendicular direction, that is
those with respect to
must exist, in the case of the
complex function the derivatives in the perpendicular direction, that is
those with respect to ![]() , must also exist, and in fact must give the
same values as the derivatives in the direction of
, must also exist, and in fact must give the
same values as the derivatives in the direction of ![]() .
.
Unlike real functions over one-dimensional domains, which can be folded around at will, complex analytic functions over two-dimensional domains are rigid objects. If one restricts such a function to a one-dimensional domain and then folds that domain around, the resulting real function over it may no longer be the restriction of a complex function to the new one-dimensional domain resulting from the folding process.