Next: Classification of Singularities Up: Weak Convergence Previous: Weak Convergence
The simplest case of what we call here weak convergence is that in which
there is absolute and uniform convergence at the unit circle to a function
which, although necessarily continuous, is not ![]() . If the
coefficients
. If the
coefficients ![]() are such that the series
are such that the series ![]() is absolutely
convergent on a single point
is absolutely
convergent on a single point ![]() of the unit circle, that is, if the
series of absolute values
of the unit circle, that is, if the
series of absolute values
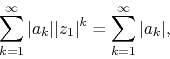
where ![]() , is convergent, then the series
, is convergent, then the series ![]() is absolutely
convergent on the whole unit circle, given that the criterion of
convergence is clearly independent of
is absolutely
convergent on the whole unit circle, given that the criterion of
convergence is clearly independent of ![]() in this case. For the same
reason, the series in uniformly convergent and thus converges to a
continuous function over the whole unit circle. Therefore the
corresponding FC Fourier series are also absolutely and uniformly
convergent to continuous functions
in this case. For the same
reason, the series in uniformly convergent and thus converges to a
continuous function over the whole unit circle. Therefore the
corresponding FC Fourier series are also absolutely and uniformly
convergent to continuous functions
![]() and
and
![]() over their whole domain.
over their whole domain.
In this case, although the function ![]() must have at least one
singularity on the unit circle, since the series
must have at least one
singularity on the unit circle, since the series ![]() converges
everywhere that function is still well defined over the whole unit circle,
and by Abel's theorem [2] the
converges
everywhere that function is still well defined over the whole unit circle,
and by Abel's theorem [2] the ![]() limit of the
function
limit of the
function ![]() from the interior of the unit disk to the unit circle
exists at all points of that circle. It follows that the singularity or
singularities of
from the interior of the unit disk to the unit circle
exists at all points of that circle. It follows that the singularity or
singularities of ![]() at the unit circle must not involve divergences to
infinity. We will classify such singularities, at which the complex
function is still well-defined, although non-analytic, as soft
singularities. Singularities at which the complex function diverges to
infinity or cannot be defined at all will be called hard
singularities.
at the unit circle must not involve divergences to
infinity. We will classify such singularities, at which the complex
function is still well-defined, although non-analytic, as soft
singularities. Singularities at which the complex function diverges to
infinity or cannot be defined at all will be called hard
singularities.
Since they are convergent everywhere, in this case all DP trigonometric
series are DP Fourier series of the continuous function obtained on the
unit circle by the ![]() limit of the real and imaginary parts of
limit of the real and imaginary parts of
![]() from within the unit disk. In short, we have established that
weakly-convergent FC pairs of DP Fourier series that converge absolutely
and thus uniformly must correspond to inner analytic functions that have
only soft singularities on the unit circle. In fact, this would be true of
any FC pair of DP Fourier series that simply converges weakly everywhere
over the unit circle.
from within the unit disk. In short, we have established that
weakly-convergent FC pairs of DP Fourier series that converge absolutely
and thus uniformly must correspond to inner analytic functions that have
only soft singularities on the unit circle. In fact, this would be true of
any FC pair of DP Fourier series that simply converges weakly everywhere
over the unit circle.
Most of the time this situation can be determined fairly easily in terms
of the coefficients ![]() of the series. If there is a positive real
constant
of the series. If there is a positive real
constant ![]() , a strictly positive number
, a strictly positive number ![]() and an integer
and an integer
![]() such that for
such that for ![]() the absolute values of the coefficients
can be bounded as
the absolute values of the coefficients
can be bounded as
then the asymptotic part of the series of the absolute values of the terms
of ![]() , which is a sum of positive terms and thus increases
monotonically, can be bounded from above by a convergent asymptotic
integral, as shown in Section A.1 of
Appendix A, and thus that series converges. It follows that
the
, which is a sum of positive terms and thus increases
monotonically, can be bounded from above by a convergent asymptotic
integral, as shown in Section A.1 of
Appendix A, and thus that series converges. It follows that
the ![]() series is absolutely and uniformly convergent on the whole
unit circle, and therefore so are the two corresponding DP Fourier series.
series is absolutely and uniformly convergent on the whole
unit circle, and therefore so are the two corresponding DP Fourier series.
If the coefficients tend to zero as a power when ![]() , then it is
easy to see that the limiting function defined by the series cannot be
, then it is
easy to see that the limiting function defined by the series cannot be
![]() . Since every term-wise derivative of the Fourier series with
respect to
. Since every term-wise derivative of the Fourier series with
respect to ![]() adds a factor of
adds a factor of ![]() to the coefficients, a decay to
zero as
to the coefficients, a decay to
zero as
![]() with
with
![]() guarantees that
we may take only up to
guarantees that
we may take only up to ![]() term-by-term derivatives and still end up with
an absolutely and uniformly convergent series. With
term-by-term derivatives and still end up with
an absolutely and uniformly convergent series. With ![]() differentiations
the resulting series might still converge almost everywhere, but that is
not certain, and typically at least one of the two DP series in the FC
pair will diverge somewhere. With
differentiations
the resulting series might still converge almost everywhere, but that is
not certain, and typically at least one of the two DP series in the FC
pair will diverge somewhere. With ![]() differentiations the series
differentiations the series
![]() is sure to diverge everywhere, and the two DP series in the FC
pair are sure to diverge almost everywhere, since the coefficients no
longer go to zero as
is sure to diverge everywhere, and the two DP series in the FC
pair are sure to diverge almost everywhere, since the coefficients no
longer go to zero as ![]() .
.
It is easy to see that the points where one of the limiting functions
![]() and
and
![]() is not differentiable, or
those at which there is a singularity in one of its derivatives, must be
points where
is not differentiable, or
those at which there is a singularity in one of its derivatives, must be
points where ![]() is singular. At any point of the unit circle where
is singular. At any point of the unit circle where
![]() is analytic it not only is continuous but also infinitely
differentiable. We see therefore that the set of points of the unit circle
where
is analytic it not only is continuous but also infinitely
differentiable. We see therefore that the set of points of the unit circle
where
![]() and
and
![]() or their derivatives of
any order have singularities of any kind must be exactly the same set of
points where
or their derivatives of
any order have singularities of any kind must be exactly the same set of
points where ![]() has singularities on that circle. In our present case,
since the functions must be continuous, these singularities can only be
points of non-differentiability of the functions or points where some of
their higher-order derivatives do not exist.
has singularities on that circle. In our present case,
since the functions must be continuous, these singularities can only be
points of non-differentiability of the functions or points where some of
their higher-order derivatives do not exist.
We conclude therefore that the cases in which the convergence is not
strong but is still absolute and uniform are easily characterized. The
really difficult cases regarding convergence are, therefore, those in
which the series are not absolutely or uniformly convergent on the unit
circle. These are cases in which ![]() goes to zero as
goes to zero as ![]() or slower
as
or slower
as ![]() , as shown in Section A.1 of
Appendix A. We will refer to these cases as those of very weak convergence. In this case the Fourier series can converge to
discontinuous functions, and
, as shown in Section A.1 of
Appendix A. We will refer to these cases as those of very weak convergence. In this case the Fourier series can converge to
discontinuous functions, and ![]() will typically diverge at some points
of the unit circle, at which
will typically diverge at some points
of the unit circle, at which ![]() has divergent limits and therefore
hard singularities. In order to discuss this case we must first establish
a few simple preliminary facts, leading to a classification of
singularities according to their severity.
has divergent limits and therefore
hard singularities. In order to discuss this case we must first establish
a few simple preliminary facts, leading to a classification of
singularities according to their severity.