Next: Absolute and Uniform Convergence Up: Fourier Theory on the Previous: Introduction
In the previous paper [1] we discussed the issue of the convergence of FC pairs of DP Fourier series such as
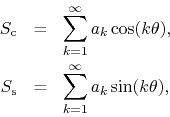
with real Fourier coefficients ![]() , for
, for ![]() in the periodic
interval
in the periodic
interval ![]() , and of the corresponding complex power series
, and of the corresponding complex power series
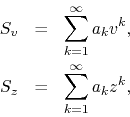
where
![]() and
and ![]() , in two extreme cases, those of
strong divergence and strong convergence. We established that, in these
extreme cases, either the convergence/divergence of
, in two extreme cases, those of
strong divergence and strong convergence. We established that, in these
extreme cases, either the convergence/divergence of ![]() or the
existence/absence of singularities of the analytic function
or the
existence/absence of singularities of the analytic function ![]() that
that
![]() converges to can be used to determine the convergence or
divergence of
converges to can be used to determine the convergence or
divergence of ![]() and of the corresponding DP Fourier series over the
whole unit circle of the complex plane.
and of the corresponding DP Fourier series over the
whole unit circle of the complex plane.
Specifically, we established that the divergence of ![]() , or the
existence of a singularity of
, or the
existence of a singularity of ![]() , at any single point strictly within
the open unit disk, implies that
, at any single point strictly within
the open unit disk, implies that ![]() diverges everywhere on the unit
circle, and that the corresponding FC pair of DP Fourier series diverge
almost everywhere on the periodic interval. This is what we call strong
divergence. To complement this we established that the convergence of
diverges everywhere on the unit
circle, and that the corresponding FC pair of DP Fourier series diverge
almost everywhere on the periodic interval. This is what we call strong
divergence. To complement this we established that the convergence of
![]() at a single point strictly outside the closed unit disk, or the
absence of singularities of
at a single point strictly outside the closed unit disk, or the
absence of singularities of ![]() on that disk, implies that
on that disk, implies that ![]() converges to a
converges to a ![]() function everywhere on the unit circle, and
that the corresponding FC pair of DP Fourier series converge to
function everywhere on the unit circle, and
that the corresponding FC pair of DP Fourier series converge to
![]() real functions everywhere on the periodic interval. This is
what we call strong convergence.
real functions everywhere on the periodic interval. This is
what we call strong convergence.
If the series ![]() constructed from an FC pair of DP trigonometric
series converges on at least one point on the unit circle, but does not
converge at any points strictly outside the closed unit disk, then the
situation is significantly more complex. We will see, however, that in
essence it can still be completely determined, with some limitations on
the set of series involved when establishing the results. We will refer to
this situation as the case of weak convergence. In this situation
the maximum disk of convergence of the complex power series
constructed from an FC pair of DP trigonometric
series converges on at least one point on the unit circle, but does not
converge at any points strictly outside the closed unit disk, then the
situation is significantly more complex. We will see, however, that in
essence it can still be completely determined, with some limitations on
the set of series involved when establishing the results. We will refer to
this situation as the case of weak convergence. In this situation
the maximum disk of convergence of the complex power series ![]() is the
open unit disk, and therefore this series converges strongly to an
analytic function
is the
open unit disk, and therefore this series converges strongly to an
analytic function ![]() strictly within that disk. As is well known, it
can be shown that in this case the function
strictly within that disk. As is well known, it
can be shown that in this case the function ![]() must have at least one
singularity on the unit circle.
must have at least one
singularity on the unit circle.
In terms of the convergence of the series, however, the situation on the
unit circle remains undefined. The series ![]() may converge or diverge
at various points on that circle. The function
may converge or diverge
at various points on that circle. The function ![]() cannot be analytic
on the whole unit circle, since there must be at least one point on that
circle where it has a singularity, in the sense that it is not analytic at
that point. This singularity can be of various types, and does not
necessarily mean that the function
cannot be analytic
on the whole unit circle, since there must be at least one point on that
circle where it has a singularity, in the sense that it is not analytic at
that point. This singularity can be of various types, and does not
necessarily mean that the function ![]() is not defined at its location.
In fact, it is still possible for
is not defined at its location.
In fact, it is still possible for ![]() to exist everywhere and to be
analytic almost everywhere on the unit circle. No general convergence
theorem is available for this case, and the analysis must be based on the
behavior of the coefficients
to exist everywhere and to be
analytic almost everywhere on the unit circle. No general convergence
theorem is available for this case, and the analysis must be based on the
behavior of the coefficients ![]() of the series. It is, therefore,
significantly harder to obtain definite results.
of the series. It is, therefore,
significantly harder to obtain definite results.
While the case of strong divergence is characterized by the fact that the
coefficients ![]() typically diverge exponentially with
typically diverge exponentially with ![]() , and the
case of strong convergence by the fact that they typically go to zero
exponentially with
, and the
case of strong convergence by the fact that they typically go to zero
exponentially with ![]() , in the case of weak convergence the typical
behavior is that the coefficients go to zero as a negative power of
, in the case of weak convergence the typical
behavior is that the coefficients go to zero as a negative power of ![]() .
In most of this paper we will in fact limit the discussion to series in
which the coefficients go to zero as a negative but not necessarily
integer power of
.
In most of this paper we will in fact limit the discussion to series in
which the coefficients go to zero as a negative but not necessarily
integer power of ![]() .
.