Next: Another Regular Cosine Series Up: Appendix: Examples of Center Previous: A Regular Cosine Series
Consider the Fourier series of the Dirac delta ``function'' centered at
![]() , which we denote by
, which we denote by
![]() . We
may easily calculate its Fourier coefficients using the rules of
manipulation of
. We
may easily calculate its Fourier coefficients using the rules of
manipulation of
![]() , thus obtaining
, thus obtaining
![]() and
and
![]() for all
for all ![]() . The series is therefore the complete Fourier series given by
. The series is therefore the complete Fourier series given by
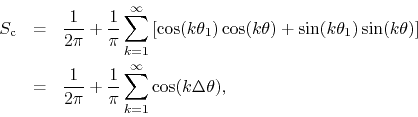
where
![]() . Apart from the constant term this
is in fact a DP cosine series on this new variable. Clearly, this series
diverges at all points in the interval
. Apart from the constant term this
is in fact a DP cosine series on this new variable. Clearly, this series
diverges at all points in the interval ![]() . Undaunted by this, we
proceed to construct the FC series, with respect to the new variable
. Undaunted by this, we
proceed to construct the FC series, with respect to the new variable
![]() , which turns out to be
, which turns out to be
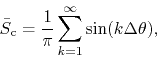
a series that is also divergent, this time almost everywhere. If we define
![]() and
and
![]() the corresponding
complex series
the corresponding
complex series ![]() is then given by
is then given by
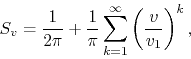
where we included the ![]() term, and the corresponding complex power
series
term, and the corresponding complex power
series ![]() is given by
is given by
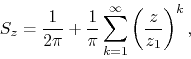
where ![]() and
and ![]() is a point over the unit circle. The
ratio test tells us that the disk of convergence of
is a point over the unit circle. The
ratio test tells us that the disk of convergence of ![]() is the unit
disk. This converges to a perfectly well-defined analytic function
strictly inside the open unit disk. If we eliminate the constant term we
get a series
is the unit
disk. This converges to a perfectly well-defined analytic function
strictly inside the open unit disk. If we eliminate the constant term we
get a series ![]() which converges to an inner analytic function
rotated by the angle
which converges to an inner analytic function
rotated by the angle ![]() ,
,
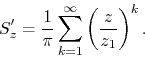
The dominant singularity is clearly at the point ![]() , so we must use
the factor
, so we must use
the factor ![]() in the construction of the corresponding center
series,
in the construction of the corresponding center
series,
![\begin{eqnarray*}
C'_{z}
& = &
(z-z_{1})S'_{z}
\\
& = &
\frac{1}{\pi}\,
...
...z_{1}}\right)^{k}
\right]
\\
& = &
-\,
\frac{1}{\pi}\,
z.
\end{eqnarray*}](img309.png)
So we see that we get a remarkably simple result, since the center series
can actually be added up exactly. We get therefore for the series ![]()
and for the series ![]()
We may now take the real and imaginary parts of the ![]() series in
order to obtain faster-converging representation of the original DP
Fourier series and its FC series. The explanation of the reasons why this
is a representation of the Dirac delta ``function'' requires taking limits
to the unit circle carefully, and since they were given in the previous
paper [1], they will not be repeated here. We have, for
series in
order to obtain faster-converging representation of the original DP
Fourier series and its FC series. The explanation of the reasons why this
is a representation of the Dirac delta ``function'' requires taking limits
to the unit circle carefully, and since they were given in the previous
paper [1], they will not be repeated here. We have, for ![]() on
the unit circle, so long as
on
the unit circle, so long as
![]() ,
,
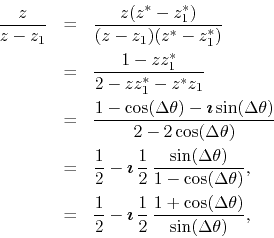
and therefore
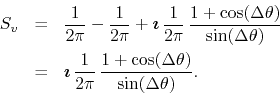
The original DP ``function'' is given by the real part, and therefore we get
which is the correct value for the Dirac delta ``function'' away from the
singular point at
![]() , and the corresponding FC function
, and the corresponding FC function
![]() is given by the imaginary
part,
is given by the imaginary
part,
which is the same result we obtained in the previous paper [1].