Solution in Vacuum

The Schwarzschild solution corresponds to the vacuum case, in which there in no matter present in the region where we are to determine the metric. For us here, this will be the solution outside the sphere that contains essentially all the matter, a region, it should be noted, that is continuously connected to radial infinity. In this empty-space case, which therefore corresponds to $T_{\mu}^{\nu}=0$, the $t$ and $r$ component equations given in Equations (24) and (25) reduce to

$$\left\{ 1 - 2\left[r\lambda'(r)\right] \right\} \,{\rm e}^{-2\lambda(r)} = 1,$$

$$\left\{ 1 + 2\left[r\nu'(r)\right] \right\} \,{\rm e}^{-2\lambda(r)} = 1,$$ (28)

so that subtracting the two equations we have that

$$\left\{ - 2\left[r\lambda'(r)\right] - 2\left[r\nu'(r)\right] \right\} \,{\rm e}^{-2\lambda(r)} = 0 \;\;\;\Rightarrow$$

$$\lambda'(r) + \nu'(r) = 0,$$ (29)

assuming that $r$ and the exponential $\exp[-2\lambda(r)]$ are never zero within the region of interest. This implies that $\lambda(r)+\nu(r)$ must be a constant $C$, and since in the $r\to\infty$ asymptotic limit both $\lambda(r)$ and $\nu(r)$ must go to zero in order for spacetime to approach the usual flat Lorentzian spacetime, it follows that the constant must be $C=0$. It therefore follows that $\nu(r)=-\lambda(r)$, and hence that we are left with the single equation for $\lambda(r)$ given by

$$\left[ 1 - 2r\lambda'(r) \right] \,{\rm e}^{-2\lambda(r)} = 1 \;\;\;\Rightarrow$$

$$\left[ r\,{\rm e}^{-2\lambda(r)} \right]' = 1 \;\;\;\Rightarrow$$

$$r \,{\rm e}^{-2\lambda(r)} - r_{1} \,{\rm e}^{-2\lambda(r_{1})} = r-r_{1},$$ (30)

where we integrated from some arbitrary reference point $r_{1}$ to $r$. We have therefore that

$$\,{\rm e}^{-2\lambda(r)} = 1 - \frac{r_{1}}{r} \left[ 1 - \,{\rm e}^{-2\lambda(r_{1})} \right].$$ (31)

If we recall that $\exp[2\lambda(r)]$ is the coefficient of $dr^{2}$ in the invariant interval, we realize that there will be a singularity in the coordinate system if and when $\exp[-2\lambda(r)]=0$, and that therefore we can take the value of the arbitrary reference point $r_{1}$ down only to the point $r_{M}$ at which this condition holds. If we make $r_{1}=r_{M}$, we have that

$$\,{\rm e}^{-2\lambda(r_{1})} = \,{\rm e}^{-2\lambda(r_{M})}$$

$$= 0,$$ (32)

and therefore our solution for $\lambda(r)$, for $r>r_{M}$, becomes

$$\,{\rm e}^{-2\lambda(r)} = 1 - \frac{r_{M}}{r},$$ (33)

where for $r\to r_{M}$ we have that $\lambda(r)\to\infty$. One can see that this expression has indeed the expected behavior of vanishing at the point $r=r_{M}$. Furthermore, since $\nu(r)=-\lambda(r)$, we also have that

$$\,{\rm e}^{2\nu(r)} = 1 - \frac{r_{M}}{r},$$ (34)

where for $r\to r_{M}$ we have that $\nu(r)\to -\infty$. This completes the determination of the metric, except for the value of $r_{M}$. Note that when one solves the gravitational field equation in this fashion one loses quite completely the explicit local connection with the sources. In a way, one of the main objectives of this paper is to recover that direct connection. In order to recover this connection in an indirect way, one takes recourse to a comparison with the Newtonian limit for large values of $r$, which implies that $r_{M}=2MG/c^{2}$, where $M$ is the total mass of the central source, as shown in [#!DiracGravity!#]. The solution is therefore valid only outside the sources, and in a region which must be continuously connected to the $r\to\infty$ asymptotic limit. The complete metric is then given by

$$ds^{2} = \left( 1 - \frac{r_{M}}{r} \right) dt^{2} ... ... \left[ d\theta^{2} + \sin^{2}(\theta) d\phi^{2} \right],$$ (35)

for $r>r_{M}$. This is indeed the well-known Schwarzschild metric. We must now verify that this solution in fact satisfies also the $\theta$ component equation and the consistency equation shown in Equations (26) and (27). That this last one is satisfied is obvious since all the components $T_{\mu}(r)$ are identically zero and therefore $\mathfrak{T}(r)\equiv 0$. In order to see this we may simply write that equation in the form

$$\mathfrak{T}(r)\left[r\nu'(r)\right] = \frac{2\omega}{1+\... ...mathfrak{T}(r) - \frac{\omega}{1+\omega}\,r\mathfrak{T}'(r),$$ (36)

which makes this fact quite plain. In order to be able to verify Equation (26) we must first calculate the relevant derivatives of the functions

$$\nu(r) = \frac{1}{2}\, \ln\!\left(\frac{r-r_{M}}{r}\right),$$

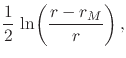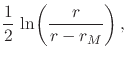$$\lambda(r) = \frac{1}{2}\, \ln\!\left(\frac{r}{r-r_{M}}\right),$$ (37)

that characterize the metric. Calculating the first derivatives of these two quantities, as well as the second derivative of $\nu(r)$, we have for the three relevant derivatives

$$r\nu'(r) = \frac{1}{2}\, \frac{r_{M}}{r-r_{M}},$$

$$r\lambda'(r) = -\, \frac{1}{2}\, \frac{r_{M}}{r-r_{M}},$$

$$r^{2}\nu''(r) = \frac{1}{2}\, \frac{r_{M}^{2}-2rr_{M}}{(r-r_{M})^{2}}.$$ (38)

Using the facts that $\lambda'(r)=-\nu'(r)$ and that $\mathfrak{T}(r)=0$ the $\theta$ component equation shown in Equation (26) can be written as

$$\left\{ r^{2}\nu''(r) + 2 \left[ r\nu'(r) \right]^{2} + 2 \left[ r\nu'(r) \right] \right\} \,{\rm e}^{-2\lambda(r)} = 0 \;\;\;\Rightarrow$$

$$r^{2}\nu''(r) + 2 \left[ r\nu'(r) \right]^{2} + 2 \left[ r\nu'(r) \right] = 0,$$ (39)

since we have that $\exp[-2\lambda(r)]\neq 0$ for $r>r_{M}$. Substituting the values of the derivatives in the expression on the left-hand side of this equation we have that

$${ \frac{1}{2}\, \frac{r_{M}^{2}-2rr_{M}}{(r-r_{M})^{2}} + \frac{2}{4}\, \frac{r_{M}^{2}}{(r-r_{M})^{2}} + \frac{2}{2}\, \frac{r_{M}}{r-r_{M}} }$$

$$= \frac{1}{2}\, \frac{r_{M}^{2}-2rr_{M}+r_{M}^{2}+2rr_{M}-2r_{M}^{2}}{(r-r_{M})^{2}}$$

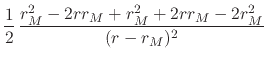$$= 0,$$ (40)

which shows that this equation is in fact satisfied. Therefore, we have now shown that all the relevant equations are satisfied by this vacuum solution, for $r>r_{M}$.

While from the point of view of the differential geometry by itself there is no singularity at $r=r_{M}$, so that it is quite possible to extend this solution to the region where $r<r_{M}$, it is not possible to do so using the Schwarzschild coordinate system. It is necessary to change to other systems of coordinates, and in doing so one loses the physical interpretations associated to the Schwarzschild coordinates. The basic problem is that, as one can immediately see in the Schwarzschild solution, when one crosses the $r_{M}$ boundary the physical roles of the radial and temporal coordinates get interchanged, due to the changes in sign of the factors multiplying $dt^{2}$ and $dr^{2}$ in the invariant interval. The interpretational issues arising from this will not be discussed here, since they are irrelevant for our current purposes. All that matters to us is the Schwarzschild solution for $r>r_{M}$, which will be used as a guide in the construction of the extended solution, valid in the presence of the localized fluid matter, and which will become the $r\to\infty$ asymptotic limit of that solution.

Figure 1: The embedding in a flat three-dimensional space of a two-dimensional spatial section through the origin of the Schwarzschild solution.

We may build a visualization of a two-dimensional spatial section of this vacuum solution through the origin by means of a isometric embedding of the two-dimensional spatial section in a three-dimensional flat space, a section of which is shown in Figure 1. In order to do this we fix $t$ at zero, $\theta$ at $\pi/2$, and let $r$ and $\phi$ vary so as to span a plane. The two-dimensional spatial interval of the resulting two-dimensional section is given by

$$d\ell^{2} = \frac{r}{r-r_{M}}\, dr^{2} + r^{2} d\phi^{2}.$$ (41)

We then introduce an embedding variable $h(r)$ such that in the flat three-dimensional embedding space spanned by $(r,\phi,h)$ we have for the element of length $d\lambda$

$$d\lambda^{2} = dr^{2} + r^{2} d\phi^{2} + dh^{2},$$ (42)

using the cylindrical system of coordinates $(r,\phi,h)$. If we fix $\phi$ at some arbitrary value, making $d\phi=0$, and impose that the length element $d\lambda$ is given by the physical length of the Schwarzschild solution associated to a variation $dr$,

$$d\lambda^{2} = \frac{r}{r-r_{M}}\, dr^{2},$$ (43)

then in the $(r,h)$ plane of the embedding space, which is shown in Figure 1, we have that

$$dr^{2} + dh^{2} = \frac{r}{r-r_{M}}\, dr^{2} \;\;\;\Rightarrow$$

$$dh^{2} = \frac{r_{M}}{r-r_{M}}\, dr^{2}.$$ (44)

This relation between $dh$ and $dr$ can be integrated to yield a function $h(r)$, and therefore a two-dimensional curved surface within the three-dimensional flat embedding space, which is described by the variables $r$ and $\phi$. The metric geometry over such a surface is that given by the Schwarzschild solution for the section through the origin, and therefore this is an isometric embedding of that two-dimensional geometry. Doing the integration we have

$$dh = \frac{\sqrt{r_{M}}}{\sqrt{r-r_{M}}}\, dr \;\;\;\Rightarrow$$

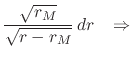$$h(r) = 2\sqrt{r_{M}} \sqrt{r-r_{M}},$$ (45)

where we integrated on $r$, choosing the integration constant in such a way that $h(r_{M})=0$. If we invert this relation a parabola results, giving $r$ in terms of $h$,

$$r(h) = r_{M} + \frac{h^{2}}{4r_{M}},$$ (46)

for all $\phi$. If we rotate the tilted parabola shown on the right-hand side of Figure 1 around the vertical $h$ axis, that is, if we now let $\phi$ vary from $0$ to $2\pi$, this simple embedding illustrates the two-dimensional form of the mouth of the famous ``wormhole'', immediately outside the event horizon located at $r=r_{M}$, that is, for $r\geq r_{M}$ and $h\geq 0$.

For future comparison with the solution in the presence of matter we record here the values of the following quantities in the case of the Schwarzschild solution. This vacuum solution is characterized by the set of quantities

$$\,{\rm e}^{2\nu(r)} = \frac{r-r_{M}}{r},$$ (47)

$$\,{\rm e}^{2\lambda(r)} = \frac{r}{r-r_{M}},$$ (48)

$$r\nu'(r) = \frac{1}{2}\, \frac{r_{M}}{r-r_{M}},$$ (49)

$$r\lambda'(r) = -\, \frac{1}{2}\, \frac{r_{M}}{r-r_{M}},$$ (50)

$$r\left[r\nu'(r)\right]'(r) = -\, \frac{1}{2}\, \frac{rr_{M}}{(r-r_{M})^{2}},$$ (51)

where we used, in order to get from Equation (38) to Equation (51), the fact that

$$r \left[ r\nu'(r) \right]' = r^{2}\nu''(r) + r\nu'(r).$$ (52)

These quantities are to be interpreted as the asymptotic values of the corresponding quantities for the solution in the presence of fluid matter. This completes the discussion of the Schwarzschild solution, and therefore we proceed now to the discussion of the solution in the presence of localized fluid matter.