The Convergence Condition

Given an arbitrary zero-average integrable real function $f(\theta)$ defined on the unit circle, the necessary and sufficient condition for the convergence of its Fourier series at the point $\theta$ is stated very simply as the condition that

$$\lim_{N\to\infty} R_{N}^{F}(\theta) = 0,$$ (89)

where $R_{N}^{F}(\theta)$ is the remainder of that Fourier series, as given in Section 6. According to what was shown in that Section, in terms of the integral operator ${\cal D}_{\rm c}[N,g(\theta)]$ this translates therefore as the condition that

$$\lim_{N\to\infty} {\cal D}_{\rm c}[N,g(\theta)] = 0,$$ (90)

where $g(\theta)$ is the Fourier-conjugate function of $f(\theta)$, which is given by the compact Hilbert transform ${\cal H}_{\rm c}[f(\theta)]$, leading therefore to the composition of the two operators,

$$\lim_{N\to\infty} {\cal D}_{\rm c}\!\left[\rule{0em}{2ex}N,{\cal H}_{\rm c}[f(\theta)]\right] = 0.$$ (91)

Equivalently, we may define the linear integral operator ${\cal D}_{\rm r}[N,f(\theta)]$ to be this composition of ${\cal D}_{\rm c}[N,f(\theta)]$ with ${\cal H}_{\rm c}[f(\theta)]$,

$${\cal D}_{\rm r}[N,f(\theta)] = {\cal D}_{\rm c}\!\left[\rule{0em}{2ex}N,{\cal H}_{\rm c}[f(\theta)]\right],$$ (92)

that therefore maps $f(\theta)$ directly onto the $N^{\rm th}$ remainder of its Fourier series,

$$R_{N}^{F}(\theta) = {\cal D}_{\rm r}[N,f(\theta)],$$ (93)

so that the convergence condition of the Fourier series of $f(\theta)$ can now be written as

$$\lim_{N\to\infty} {\cal D}_{\rm r}[N,f(\theta)] = 0.$$ (94)

Combining the integration kernels of the operators ${\cal D}_{\rm c}[N,f(\theta)]$, given in Equation (83), and ${\cal H}_{\rm c}[f(\theta)]$, given in Equation (27), we may write an integration kernel for the operator ${\cal D}_{\rm r}[N,f(\theta)]$, which is not given explicitly, but rather remains expressed as an integral over the unit circle,

$$K_{{\cal D}_{\rm r}}(N,\theta,\theta_{1}) = \frac{1}{4\pi... ... \sin\!\left[\rule{0em}{2ex}(\theta'-\theta_{1})/2\right] },$$ (95)

in terms of which the action of the operator ${\cal D}_{\rm r}[N,f(\theta)]$ on $f(\theta)$ is given by

$${\cal D}_{\rm r}[N,f(\theta)] = \mbox{\rm PV}\!\!\int_{-\... ...}\, K_{{\cal D}_{\rm r}}(N,\theta,\theta_{1}) f(\theta_{1}).$$ (96)

Note that at this point it is not clear whether or not the integration kernel depends only on the difference $\theta-\theta_{1}$. We will prove that it does, and we will also write it in a somewhat more convenient form. In this section we will prove the following theorem.

Theorem 6   : Given an arbitrary zero-average integrable real function $f(\theta)$ defined on the unit circle, the necessary and sufficient condition for the convergence of its Fourier series at the point $\theta$ is as follows:

$$\lim_{N\to\infty} \mbox{\rm PV}\!\!\int_{-\pi}^{\pi}d\thet... ..._{{\cal D}_{\rm r}}(N,\theta-\theta_{1}) f(\theta_{1}) = 0,$$ (97)

where the integration kernel is given by

$${ K_{{\cal D}_{\rm r}}(N,\theta-\theta_{1}) }$$

$$= \frac {\cos\!\left[\rule{0em}{2ex}(N+1)(\theta-\theta_{1})/2\righ... ...} { \cos\!\left[\rule{0em}{2ex}(\theta-\theta_{1})/2\right] - \cos(\theta') } +$$

$$\hspace{1.75em} + \frac {\cos\!\left[\rule{0em}{2ex}N(\theta-\the... ... } { \cos\!\left[\rule{0em}{2ex}(\theta-\theta_{1})/2\right] - \cos(\theta') }.$$ (98)

Note that the two integrals in this form of the condition are almost identical, differing only by the exchange of $N$ for $N+1$. Note also that the integrands of these integrals are singular at the points $\theta'=\pm(\theta-\theta_{1})/2$. Note, finally, that the condition in Equation (97) means that the remainder $R_{N}^{F}(\theta)$ must exist, being a finite number for each $N$, as well as that its $N\to\infty$ limit must be zero. The existence of the remainder is, of course, equivalent to the existence of the integrals involved.

Proof 6.1   :

We start by making in the integral in Equation (95) the transformation of variables

$$\theta'' = \theta' - \frac{\theta+\theta_{1}}{2} \;\;\;\Rightarrow$$

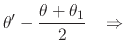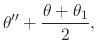$$\theta' = \theta'' + \frac{\theta+\theta_{1}}{2},$$ (99)

which implies that

$$\theta'-\theta = \theta'' - \frac{\theta-\theta_{1}}{2},$$

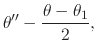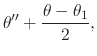$$\theta'-\theta_{1} = \theta'' + \frac{\theta-\theta_{1}}{2},$$ (100)

and which also implies that $d\theta'=d\theta''$, so that we have

$${ K_{{\cal D}_{\rm r}}(N,\theta,\theta_{1}) }$$

$$= \frac{1}{4\pi^{2}}\, \mbox{\rm PV}\!\!\int_{-\pi}^{\pi}d\theta''\... .../4\right] \sin\!\left[\rule{0em}{2ex}\theta''/2+(\theta-\theta_{1})/4\right] },$$ (101)

where $N_{1}=N+1/2$ with $N\in\{1,2,3,\ldots,\infty\}$, and where we do not have to change the integration limits since the integration runs over a circle. Note that at this point it is already clearly apparent that $K_{{\cal D}_{\rm r}}(N,\theta,\theta_{1})$ depends only on $N$ and on the difference $\theta-\theta_{1}$, and therefore from now on we will write it as $K_{{\cal D}_{\rm r}}(N,\theta-\theta_{1})$. Changing $\theta''$ back to $\theta'$ and using the notation $\gamma=(\theta-\theta_{1})/2$ we have

$$K_{{\cal D}_{\rm r}}(N,\theta-\theta_{1}) = \frac{1}{4\pi^{2}}\, \mbox{\rm PV}\!\!\int_{-\pi}^{\pi}d\theta'\,... ...\theta'-\gamma)/2\right] \sin\!\left[\rule{0em}{2ex}(\theta'+\gamma)/2\right] }$$

$$= \frac{1}{4\pi^{2}}\, \mbox{\rm PV}\!\!\int_{-\pi}^{\pi}d\theta'\, \frac{P(N,\theta',\gamma)}{Q(\theta',\gamma)},$$ (102)

where $\gamma=(\theta-\theta_{1})/2$ and $N_{1}=N+1/2$ with $N\in\{1,2,3,\ldots,\infty\}$. We will now manipulate the denominator $Q(\theta',\gamma)$ and the numerator $P(N,\theta',\gamma)$ in this integrand using trigonometric identities. We start with the denominator, and using the trigonometric identities for the sum of two angles we get

$$Q(\theta',\gamma) = \sin\!\left[\rule{0em}{2ex}(\theta'-\gamma)/2\right] \sin\!\left[\rule{0em}{2ex}(\theta'+\gamma)/2\right]$$

$$= \left[ \rule{0em}{2ex} \sin(\theta'/2) \cos(\gamma/2) - \cos(\theta'/2) \sin(\gamma/2) \right] \times$$

$$\times \left[ \rule{0em}{2ex} \sin(\theta'/2) \cos(\gamma/2) + \cos(\theta'/2) \sin(\gamma/2) \right]$$

$$= \sin^{2}(\theta'/2) \cos^{2}(\gamma/2) - \cos^{2}(\theta'/2) \sin^{2}(\gamma/2).$$ (103)

If we now write the cosines in terms of the corresponding sines we have

$$Q(\theta',\gamma) = \sin^{2}(\theta'/2) - \sin^{2}(\theta'/2) \sin^{2}(\gamma/2) +$$

$$- \sin^{2}(\gamma/2) + \sin^{2}(\theta'/2) \sin^{2}(\gamma/2)$$

$$= \sin^{2}(\theta'/2) - \sin^{2}(\gamma/2).$$ (104)

Using now the half-angle trigonometric identities we finally have

$$Q(\theta',\gamma) = \frac{1-\cos(\theta')}{2} - \frac{1-\cos(\gamma)}{2}$$

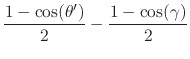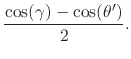$$= \frac{\cos(\gamma)-\cos(\theta')}{2}.$$ (105)

It is important to note that this is an even function of $\theta'$. Turning now to the numerator $P(N,\theta',\gamma)$, and using the trigonometric identities for the sum of two angles we get

$$P(N,\theta',\gamma) = \cos\!\left[\rule{0em}{2ex}N_{1}(\theta'-\gamma)\right] \cos\!\left[\rule{0em}{2ex}(\theta'+\gamma)/2\right]$$

$$= \left[ \rule{0em}{2ex} \cos(N_{1}\theta') \cos(N_{1}\gamma) + \sin(N_{1}\theta') \sin(N_{1}\gamma) \right] \times$$

$$\times \left[ \rule{0em}{2ex} \cos(\theta'/2) \cos(\gamma/2) - \sin(\theta'/2) \sin(\gamma/2) \right]$$

$$= \cos(N_{1}\theta') \cos(N_{1}\gamma) \cos(\theta'/2) \cos(\gamma/2) +$$

$$- \cos(N_{1}\theta') \cos(N_{1}\gamma) \sin(\theta'/2) \sin(\gamma/2) +$$

$$+ \sin(N_{1}\theta') \sin(N_{1}\gamma) \cos(\theta'/2) \cos(\gamma/2) +$$

$$- \sin(N_{1}\theta') \sin(N_{1}\gamma) \sin(\theta'/2) \sin(\gamma/2).$$ (106)

Of these four terms, the first and last ones are even on $\theta'$, and the two middle ones are odd. Since the denominator is even and the integral on $\theta'$ shown in Equation (102) is over a symmetric interval, the integrals of the two middle terms will be zero, and therefore we can ignore these two terms of the numerator. We thus obtain for our kernel

$$K_{{\cal D}_{\rm r}}(N,\theta-\theta_{1}) = \frac{1}{4\pi... ...\pi}d\theta'\, \frac{T(N,\theta',\gamma)}{Q(\theta',\gamma)},$$ (107)

where the new numerator is given by

$$T(N,\theta',\gamma) = \left\{ \rule{0em}{2.5ex} \cos\!\left[\rule{0em}{2ex}(N+1/2)\theta'\right] \cos(\theta'/2) \right\} \cos(N_{1}\gamma) \cos(\gamma/2) +$$

$$- \left\{ \rule{0em}{2.5ex} \sin\!\left[\rule{0em}{2ex}(N+1/2)\theta'\right] \sin(\theta'/2) \right\} \sin(N_{1}\gamma) \sin(\gamma/2),$$ (108)

where $\gamma=(\theta-\theta_{1})/2$ and $N_{1}=N+1/2$ with $N\in\{1,2,3,\ldots,\infty\}$. Using once again the trigonometric identities for the sum of two angles in order to work on the two expressions within pairs of curly brackets, we get

$$B_{\rm c} = \left\{ \rule{0em}{2.5ex} \cos\!\left[\rule{0em}{2ex}(N+1/2)\theta'\right] \cos(\theta'/2) \right\}$$

$$= \left[ \rule{0em}{2ex} \cos(N\theta') \cos(\theta'/2) - \sin(N\theta') \sin(\theta'/2) \right] \cos(\theta'/2)$$

$$= \rule{0em}{2ex} \cos(N\theta') \cos^{2}(\theta'/2) - \sin(N\theta') \sin(\theta'/2) \cos(\theta'/2),$$

$$B_{\rm s} = \left\{ \rule{0em}{2.5ex} \sin\!\left[\rule{0em}{2ex}(N+1/2)\theta'\right] \sin(\theta'/2) \right\}$$

$$= \left[ \rule{0em}{2ex} \sin(N\theta') \cos(\theta'/2) + \cos(N\theta') \sin(\theta'/2) \right] \sin(\theta'/2)$$

$$= \rule{0em}{2ex} \sin(N\theta') \cos(\theta'/2) \sin(\theta'/2) + \cos(N\theta') \sin^{2}(\theta'/2).$$ (109)

Using now the half-angle trigonometric identities in order to eliminate the functions $\cos(\theta'/2)$ and $\sin(\theta'/2)$ in favor of $\cos(\theta')$ and $\sin(\theta')$, we get

$$B_{\rm c} = \rule{0em}{2ex} \cos(N\theta')\, \frac{1+\cos(\theta')}{2} - \sin(N\theta')\, \frac{\sin(\theta')}{2}$$

$$= \frac{\cos(N\theta')}{2} + \frac { \cos(N\theta')\cos(\theta') - \sin(N\theta')\sin(\theta') } {2},$$

$$B_{\rm s} = \rule{0em}{2ex} \sin(N\theta')\, \frac{\sin(\theta')}{2} + \cos(N\theta')\, \frac{1-\cos(\theta')}{2}$$

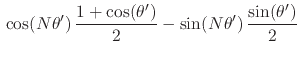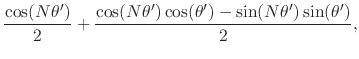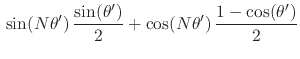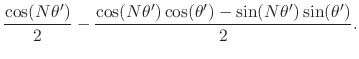$$= \frac{\cos(N\theta')}{2} - \frac { \cos(N\theta')\cos(\theta') - \sin(N\theta')\sin(\theta') } {2}.$$ (110)

Using once more the trigonometric identities for the sum of two angles we get

$$B_{\rm c} = \frac{\cos(N\theta')}{2} + \frac{\cos\!\left[\rule{0em}{2ex}(N+1)\theta'\right]}{2},$$

$$B_{\rm s} = \frac{\cos(N\theta')}{2} - \frac{\cos\!\left[\rule{0em}{2ex}(N+1)\theta'\right]}{2}.$$ (111)

We get therefore for our new numerator, using yet gain the trigonometric identities for the sum of two angles,

$$T(N,\theta',\gamma) = \frac{\cos(N\theta')}{2} \left[ \rule{0em}{2ex} \cos(N_{1}\gamma) \cos(\gamma/2) - \sin(N_{1}\gamma) \sin(\gamma/2) \right] +$$

$$+ \frac{\cos\!\left[\rule{0em}{2ex}(N+1)\theta'\right]}{2} \left[... ...ex} \cos(N_{1}\gamma) \cos(\gamma/2) + \sin(N_{1}\gamma) \sin(\gamma/2) \right]$$

$$= \frac{\cos(N\theta')\cos\!\left[\rule{0em}{2ex}(N+1)\gamma\right]}{2} + \frac{\cos\!\left[\rule{0em}{2ex}(N+1)\theta'\right]\cos(N\gamma)}{2}.$$ (112)

We therefore have for the kernel

$${ K_{{\cal D}_{\rm r}}(N,\theta-\theta_{1}) }$$

$$= \frac{1}{4\pi^{2}}\, \mbox{\rm PV}\!\!\int_{-\pi}^{\pi}d\theta'\,... ...ule{0em}{2ex}(N+1)\theta'\right]\cos(N\gamma) } { \cos(\gamma)-\cos(\theta') },$$ (113)

where $\gamma=(\theta-\theta_{1})/2$ and $N\in\{1,2,3,\ldots,\infty\}$. This is exactly the form of the integration kernel of the operator ${\cal D}_{\rm r}[N,f(\theta)]$ given in Equation (98), so that this completes the proof of Theorem 6.

Since the condition stated in Theorem 6 is a necessary and sufficient condition on the real function $f(\theta)$ for the convergence of its Fourier series, any other such condition must be equivalent to it. Note that this type of condition is not really what is usually meant by a Fourier theorem. Those are just sufficient conditions for the convergence, usually related to some fairly simple and easily identifiable characteristics of the real functions, such as continuity, differentiability, existence of lateral limits, or limited variation. However, all such Fourier theorems must be related to this condition in the sense that they must imply its validity.