next up previous
Next: Piecewise Polynomial Functions Up: Complex Analysis of Real Previous: The Dirac Delta ``Function''


Derivatives of the Delta ``Function''

The derivatives of the Dirac delta ``function'' are defined in a way which is similar to that of the delta ``function'' itself. The first condition is the same, and the second and third conditions are not really required. The crucial difference is that the fourth condition in the definition of the Dirac delta ``function'' is replaced by the second condition in the list that follows. The ``function'' $\delta^{n\prime}(\theta-\theta_{1})$ is the $n^{\rm th}$ derivative of $\delta(\theta-\theta_{1})$ with respect to $\theta$ if its defining limit $\rho\to 1_{(-)}$ satisfies the two conditions that follow.

  1. The defining limit of $\delta^{n\prime}(\theta-\theta_{1})$ tends to zero when one takes the $\rho\to 1_{(-)}$ limit while keeping $\theta\neq\theta_{1}$.

  2. Given any integrable real function $g(\theta)$ which is differentiable to the $n^{\rm th}$ order, in the $\rho\to 1_{(-)}$ limit the integral


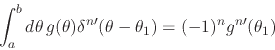    \begin{displaymath} \int_{a}^{b}d\theta\, g(\theta) \delta^{n\prime}(\theta-\theta_{1}) = (-1)^{n}g^{n\prime}(\theta_{1}) \end{displaymath} (32)

    has the value shown, for any open interval $(a,b)$ which contains the point $\theta_{1}$, where $g^{n\prime}(\theta)$ is the $n^{\rm th}$ derivative of $g(\theta)$ with respect to $\theta$.

    This is the usual form of this condition, when it is formulated in strictly real terms. However, we will impose a slight additional restriction on the real functions $g(\theta)$, by assuming that the limit to the point $z_{1}$ on the unit circle that corresponds to $\theta_{1}$, of the $n^{\rm th}$ angular derivative of the corresponding inner analytic function $w_{\gamma}(z)$, exists and is finite. Since these proper inner analytic functions are all in the same integral-differential chain, this implies that the limits to $z_{1}$ of all the inner analytic functions $w^{m\mbox{\Large$\cdot$}\!}_{\gamma}(z)$ exist, for all $0\leq m\leq n$.

The second condition above is, in fact, the fundamental property of each derivative of the delta ``function'', including the ``function'' itself in the case $n=0$. Just as in the case of the delta ``function'' itself, the additional part of the second condition, involving the inner analytic function $w_{\gamma}(z)$, consists of a weak limitation on the test functions $g(\theta)$, and does not affect the definition of the singular distributions themselves. This is certainly the case for our definitions here, since we define each one of these objects through a definite and unique inner analytic function.





In this section we will prove the following theorem.

Theorem 2   : For every strictly positive integer $n$ there exists an inner analytic function $w_{\delta^{n\prime}}(z,z_{1})$ whose real part, in the $\rho\to 1_{(-)}$ limit, converges to $\delta^{n\prime}(\theta-\theta_{1})$.

Before we attempt to prove this theorem, let us note that the proof relies on a property of angular differentiation, which was established in [#!CAoRFI!#], namely that angular differentiation is equivalent to partial differentiation with respect to $\theta$, at constant $\rho$. When we take the $\rho\to 1_{(-)}$ limit, this translates to the fact that taking the angular derivative of the inner analytic function $w(z)$ within the open unit disk corresponds to taking the derivative with respect to $\theta$, on the unit circle, of the corresponding real object.

If this derivative cannot be taken directly on the unit circle, then one can define it by taking the angular derivative of the corresponding inner analytic function and then considering the $\rho\to 1_{(-)}$ limit of the real part of the resulting function. Since analytic functions can be differentiated any number of times, the procedure can then be iterated in order to define all the higher-order derivatives with respect to $\theta$ on the unit circle. Equivalently, one can just consider traveling along the integral-differential chain indefinitely in the differentiation direction.

Consider therefore the integral-differential chain of proper inner analytic functions that is obtained from the proper inner analytic function associated to $w_{\delta}(z,z_{1})$, that is, the unique integral-differential chain to which the proper inner analytic function


$\displaystyle w_{\delta}^{0\mbox{\Large$\cdot$}\!}(z,z_{1})$ $\textstyle =$ $\displaystyle w_{\delta}(z,z_{1}) - \frac{1}{2\pi}$  
  $\textstyle =$ $\displaystyle -\, \frac{1}{\pi}\, \frac{z}{z-z_{1}}$ (33)

belongs. Consider in particular the set of proper inner analytic functions which is obtained from $w_{\delta}^{0\mbox{\Large$\cdot$}\!}(z,z_{1})$ in the differentiation direction along this chain, for which we have


$\displaystyle w_{\delta}^{n\mbox{\Large$\cdot$}\!}(z,z_{1})$ $\textstyle =$ $\displaystyle u_{\delta}^{n\prime}(\rho,\theta,\theta_{1}) + \mbox{\boldmath$\imath$} v_{\delta}^{n\prime}(\rho,\theta,\theta_{1})$  
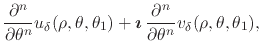  $\textstyle =$ $\displaystyle \frac{\partial^{n}}{\partial\theta^{n}} u_{\delta}(\rho,\theta,\t... ...}\, \frac{\partial^{n}}{\partial\theta^{n}} v_{\delta}(\rho,\theta,\theta_{1}),$ (34)

for all strictly positive $n$, where we recall that


\begin{displaymath} w_{\delta}(z,z_{1}) = u_{\delta}(\rho,\theta,\theta_{1}) + \mbox{\boldmath$\imath$} v_{\delta}(\rho,\theta,\theta_{1}). \end{displaymath} (35)

We will now prove that in the $\rho\to 1_{(-)}$ limit we have


\begin{displaymath} \delta^{n\prime}(\theta-\theta_{1}) = \lim_{\rho\to 1_{(-)}} u_{\delta}^{n\prime}(\rho,\theta,\theta_{1}), \end{displaymath} (36)

for $n\in\{1,2,3,\ldots,\infty\}$, or, equivalently, that we have for the inner analytic function $w_{\delta^{n\prime}}(z,z_{1})$ associated to the derivative $\delta^{n\prime}(\theta-\theta_{1})$


\begin{displaymath} w_{\delta^{n\prime}}(z,z_{1}) = w_{\delta}^{n\mbox{\Large$\cdot$}\!}(z,z_{1}), \end{displaymath} (37)

for $n\in\{1,2,3,\ldots,\infty\}$. We are now ready to prove the theorem, as stated in Equation (36). Let us first prove, however, that the first condition holds for all the derivatives of the delta ``function''.

Proof 2.1   :

Since $w_{\delta}(z,z_{1})$ has a single singular point at $z_{1}$, the same is true for all its angular derivatives. Therefore the $\rho\to 1_{(-)}$ limit of all the angular derivatives exists everywhere within the open interval of the unit circle that excludes the point $\theta_{1}$. Since $u_{\delta}(1,\theta,\theta_{1})$ is identically zero within this interval, and since angular differentiation within the open unit disk corresponds to differentiation with respect to $\theta$ on the unit circle, so that we have


\begin{displaymath} u_{\delta}^{n\prime}(1,\theta,\theta_{1}) = \frac{\partial^{n}}{\partial\theta^{n}} u_{\delta}(1,\theta,\theta_{1}), \end{displaymath} (38)

for $n\in\{1,2,3,\ldots,\infty\}$, it follows at once that


$\displaystyle u_{\delta}^{n\prime}(1,\theta,\theta_{1})$ $\textstyle =$ $\displaystyle 0 \;\;\;\Rightarrow$  
$\displaystyle \lim_{\rho\to 1_{(-)}} u_{\delta}^{n\prime}(\rho,\theta,\theta_{1})$ $\textstyle =$ $\displaystyle 0,$ (39)

for $n\in\{1,2,3,\ldots,\infty\}$, everywhere but at the singular point $\theta_{1}$, for all values of $n$. This establishes that the first condition holds.





Let us now prove that the second condition, which relates directly to the singular point, holds, leading to the result as stated in Equation (36).

Proof 2.2   :

In order to do this, we start with the case $n=1$, and consider the following real integral on the circle of radius $\rho<1$, which we integrate by parts, noting that the integrated term is zero because we are integrating on a circle,


\begin{displaymath} \int_{-\pi}^{\pi}d\theta\, u_{\gamma}(\rho,\theta) \left[... ...ma}(\rho,\theta) \right] u_{\delta}(\rho,\theta,\theta_{1}), \end{displaymath} (40)

where $w_{\gamma}(z)=u_{\gamma}(\rho,\theta)+\mbox{\boldmath$\imath$}v_{\gamma}(\rho,\theta)$ is the inner analytic function associated to $g(\theta)$. Note that the partial derivatives involved certainly exist, since both $u_{\delta}(\rho,\theta,\theta_{1})$ and $u_{\gamma}(\rho,\theta)$ are the real parts of inner analytic functions. If we now take the $\rho\to 1_{(-)}$ limit, on the right-hand side we recover the Dirac delta ``function'' on the unit circle, and therefore we have


$\displaystyle \int_{-\pi}^{\pi}d\theta\, g(\theta) \left[ \lim_{\rho\to 1_{(-)}} \frac{\partial}{\partial\theta} u_{\delta}(\rho,\theta,\theta_{1}) \right]$ $\textstyle =$ $\displaystyle - \int_{-\pi}^{\pi}d\theta\, \left[ \frac{d}{d\theta} g(\theta) \right] \delta(\theta-\theta_{1})$  
  $\textstyle =$ $\displaystyle (-1)\, g'(\theta_{1}),$ (41)

so long as $g(\theta)$ is differentiable, were we used the fundamental property of the Dirac delta ``function''. We thus obtain the relation for the derivative of the delta ``function'',


\begin{displaymath} \int_{-\pi}^{\pi}d\theta\, g(\theta) \delta'(\theta-\theta_{1}) = (-1)\, g'(\theta_{1}), \end{displaymath} (42)

where


\begin{displaymath} \delta'(\theta-\theta_{1}) = \lim_{\rho\to 1_{(-)}} \frac{\partial}{\partial\theta} u_{\delta}(\rho,\theta,\theta_{1}). \end{displaymath} (43)

We may therefore write that


\begin{displaymath} \delta'(\theta-\theta_{1}) = \lim_{\rho\to 1_{(-)}} u'_{\delta}(\rho,\theta,\theta_{1}). \end{displaymath} (44)

In this way we have obtained the result for $\delta'(\theta-\theta_{1})$ by using the known result for $\delta(\theta-\theta_{1})$. We may now repeat this procedure to obtain the result for $\delta^{2\prime}(\theta-\theta_{1})$ from the result for $\delta'(\theta-\theta_{1})$, and therefore from the result for $\delta(\theta-\theta_{1})$. We simply consider the following real integral on the circle of radius $\rho<1$, which we again integrate by parts, recalling that the integrated term is zero because we are integrating on a circle,


\begin{displaymath} \int_{-\pi}^{\pi}d\theta\, u_{\gamma}(\rho,\theta) \left[... ...a}(\rho,\theta) \right] u'_{\delta}(\rho,\theta,\theta_{1}). \end{displaymath} (45)

If we now take the $\rho\to 1_{(-)}$ limit, on the right-hand side we recover the first derivative of the Dirac delta ``function'' on the unit circle, and therefore we have


$\displaystyle \int_{-\pi}^{\pi}d\theta\, g(\theta) \left[ \lim_{\rho\to 1_{(-)}} \frac{\partial}{\partial\theta} u'_{\delta}(\rho,\theta,\theta_{1}) \right]$ $\textstyle =$ $\displaystyle - \int_{-\pi}^{\pi}d\theta\, \left[ \frac{d}{d\theta} g(\theta) \right] \delta'(\theta-\theta_{1})$  
  $\textstyle =$ $\displaystyle (-1)^{2}g^{2\prime}(\theta_{1}),$ (46)

so long as $g(\theta)$ is differentiable to second order, were we used the fundamental property of the first derivative of the Dirac delta ``function''. We thus obtain the relation for the second derivative of the delta ``function'',


\begin{displaymath} \int_{-\pi}^{\pi}d\theta\, g(\theta) \delta^{2\prime}(\theta-\theta_{1}) = (-1)^{2}g^{2\prime}(\theta_{1}), \end{displaymath} (47)

where


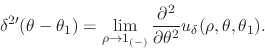\begin{displaymath} \delta^{2\prime}(\theta-\theta_{1}) = \lim_{\rho\to 1_{(-... ...^{2}}{\partial\theta^{2}} u_{\delta}(\rho,\theta,\theta_{1}). \end{displaymath} (48)

We may therefore write that


\begin{displaymath} \delta^{2\prime}(\theta-\theta_{1}) = \lim_{\rho\to 1_{(-)}} u_{\delta}^{2\prime}(\rho,\theta,\theta_{1}). \end{displaymath} (49)

Clearly, this procedure can be iterated $n$ times, thus resulting in the relation


\begin{displaymath} \delta^{n\prime}(\theta-\theta_{1}) = \lim_{\rho\to 1_{(-)}} u_{\delta}^{n\prime}(\rho,\theta,\theta_{1}), \end{displaymath} (50)

for $n\in\{1,2,3,\ldots,\infty\}$. Note that all the derivatives with respect to $\theta$ involved in the argument exist, for arbitrarily high orders, since both $u_{\delta}(\rho,\theta,\theta_{1})$ and $u_{\gamma}(\rho,\theta)$ are the real parts of inner analytic functions, and thus are infinitely differentiable on both arguments.

We may now formalize the proof using finite induction. We thus assume the results for the case $n-1$,


$\displaystyle \delta^{(n-1)\prime}(\theta-\theta_{1})$ $\textstyle =$ $\displaystyle \lim_{\rho\to 1_{(-)}} u_{\delta}^{(n-1)\prime}(\rho,\theta,\theta_{1}),$  
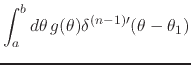$\displaystyle \int_{a}^{b}d\theta\, g(\theta) \delta^{(n-1)\prime}(\theta-\theta_{1})$ $\textstyle =$ $\displaystyle (-1)^{n-1}g^{(n-1)\prime}(\theta_{1}),$ (51)

and proceed to examine the next case. We consider therefore the following real integral on the circle of radius $\rho<1$, which we integrate by parts, recalling once more that the integrated term is zero because we are integrating on a circle,


\begin{displaymath} \int_{-\pi}^{\pi}d\theta\, u_{\gamma}(\rho,\theta) \left[... ...a) \right] u_{\delta}^{(n-1)\prime}(\rho,\theta,\theta_{1}). \end{displaymath} (52)

If we now take the $\rho\to 1_{(-)}$ limit, on the right-hand side we recover the $(n-1)^{\rm th}$ derivative of the Dirac delta ``function'' on the unit circle, and therefore we have


$\displaystyle \int_{-\pi}^{\pi}d\theta\, g(\theta) \left[ \lim_{\rho\to 1_{(-)}... ...rtial}{\partial\theta} u_{\delta}^{(n-1)\prime}(\rho,\theta,\theta_{1}) \right]$ $\textstyle =$ $\displaystyle - \int_{-\pi}^{\pi}d\theta\, \left[ \frac{d}{d\theta} g(\theta) \right] \delta^{(n-1)\prime}(\theta-\theta_{1})$  
  $\textstyle =$ $\displaystyle (-1)^{n}\, g^{n\prime}(\theta_{1}),$ (53)

so long as $g(\theta)$ is differentiable to order $n$, were we used the fundamental property of the $(n-1)^{\rm th}$ derivative of the Dirac delta ``function''. We thus obtain the relation for the $n^{\rm th}$ derivative of the delta ``function'',


\begin{displaymath} \int_{-\pi}^{\pi}d\theta\, g(\theta) \delta^{n\prime}(\theta-\theta_{1}) = (-1)^{n}\, g^{n\prime}(\theta_{1}), \end{displaymath} (54)

where


\begin{displaymath} \delta^{n\prime}(\theta-\theta_{1}) = \lim_{\rho\to 1_{(-... ...^{n}}{\partial\theta^{n}} u_{\delta}(\rho,\theta,\theta_{1}). \end{displaymath} (55)

We may therefore write that, by finite induction,


\begin{displaymath} \delta^{n\prime}(\theta-\theta_{1}) = \lim_{\rho\to 1_{(-)}} u_{\delta}^{n\prime}(\rho,\theta,\theta_{1}), \end{displaymath} (56)

for $n\in\{1,2,3,\ldots,\infty\}$. We have therefore completed the proof of Theorem 2.





It is important to note that, just as in the case of the Dirac delta ``function'', when we adopt as the definition of the $n^{\rm th}$ derivative of the delta ``function'' the $\rho\to 1_{(-)}$ limit of the real part of the inner analytic function $w_{\delta}^{n\mbox{\Large$\cdot$}\!}(z,z_{1})$, for $n\in\{1,2,3,\ldots,\infty\}$, the limitations imposed on the test functions $g(\theta)$ and on the corresponding inner analytic functions $w_{\gamma}(z)$ become irrelevant. In fact, these definitions stand by themselves, and are independent of any set of test functions. Not only one can use them for any inner analytic functions derived from integrable real functions, but one can do this for any inner analytic function $w(z)$, regardless of whether or not it corresponds to an integrable real function, so long as the $\rho\to 1_{(-)}$ limit of the corresponding real part $u(\rho,\theta)$ exists almost everywhere. Just as in the case of the Dirac delta ``function'', whenever the $\rho\to 1_{(-)}$ limit of the real integral


\begin{displaymath} \int_{-\pi}^{\pi}d\theta\, \rho\, u(\rho,\theta) u_{\delta}^{n\prime}(\rho,\theta,\theta_{1}), \end{displaymath} (57)

exists, it defines the action of the $n^{\rm th}$ derivative of the delta ``function'' on that particular real object.

It is also interesting to observe that, just as in the case of the Dirac delta ``function'', it is true that its derivatives of all orders, although they are not simply integrable real functions, are in fact integrable real objects, even if they are related to inner analytic functions with non-integrable hard singularities. Just as is the case for the inner analytic function associated to the delta ``function'' itself, the poles of the proper inner analytic functions associated to the derivatives are always oriented in such a way that one can approach the singularities along the unit circle while keeping the real parts of the functions equal to zero, a fact that allows one to define the integrals on $\theta$ of the real parts via the $\rho\to 1_{(-)}$ limit4. Just as in the case of the delta ``function'', the Fourier-conjugate functions of the derivatives are simply non-integrable real functions. This fact provides the first hint that there must be some relation of such non-integrable real functions with corresponding inner analytic functions.

In the development presented in [#!CAoRFI!#] the real functions were represented by their Fourier coefficients, and the inner analytic functions by their Taylor coefficients. The same can be done in our case here. Starting from the power series for $w_{\delta}^{0\mbox{\Large$\cdot$}\!}(z,z_{1})$ given in Equation (28), we can see that the definition of the angular derivative implies that we have for the inner analytic functions associated to the derivatives of the delta ``function'',


\begin{displaymath} w_{\delta}^{n\mbox{\Large$\cdot$}\!}(z,z_{1}) = \frac{1}{... ... \mbox{\boldmath$\imath$} \sin(k\theta_{1}) \right] z^{k}, \end{displaymath} (58)

for $n\in\{1,2,3,\ldots,\infty\}$, so that the corresponding Taylor coefficients are given by $c_{0}^{(n)}=0$ and


\begin{displaymath} c_{k}^{(n)} = \frac{\mbox{\boldmath$\imath$}^{n}k^{n}}{\p... ...}) - \mbox{\boldmath$\imath$}\, \sin(k\theta_{1}) \right], \end{displaymath} (59)

for $n\in\{1,2,3,\ldots,\infty\}$, and where $k\in\{1,2,3,\ldots,\infty\}$. The identification of the Fourier coefficients $\alpha_{k}^{(n)}$ and $\beta_{k}^{(n)}$ will now depend on the parity of $n$.

Once we have the Dirac delta ``function'' and all its derivatives, both as inner analytic functions and as the corresponding real objects, we may consider collections of such singular objects, with their singularities located at all the possible points of the periodic interval $[-\pi,\pi]$, as well as arbitrary linear combinations of some or all of them. There is a well-known theorem of the Schwartz theory of distributions [#!DTSchwartz!#,#!DTLighthill!#] which states that any distribution which is singular at a given point $\theta_{1}$ can be expressed as a linear combination of the Dirac delta ``function'' $\delta(\theta-\theta_{1})$ and its derivatives of arbitrarily high orders $\delta^{n\prime}(\theta-\theta_{1})$.

Since, as was observed in [#!CAoRFI!#], the set of all inner analytic functions forms a vector space over the field of complex numbers, it is immediately apparent that we may assemble such linear combinations within the space of inner analytic functions. Therefore, the set of distributions formed by the delta ``functions'' and all their derivatives, as defined here, with their singularities located at all possible points of the unit circle, constitutes a complete basis that spans the space of all possible singular Schwartz distributions defined in a compact domain. We may conclude therefore that the whole space of Schwartz distributions in a compact domain is contained within the set of inner analytic functions.

It is interesting to note that, since we have the inner analytic function that corresponds to the delta ``function'' in explicit form, we are in a position to perform simple calculations in order to obtain in explicit form the inner analytic functions that correspond to the first few derivatives of the delta ``function''. For example, a few simple and straightforward calculations lead to the following proper inner analytic functions,


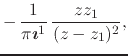$\displaystyle w_{\delta^{1\prime}}(z,z_{1})$ $\textstyle =$ $\displaystyle -\, \frac{1}{\pi\mbox{\boldmath$\imath$}^{1}}\, \frac {zz_{1}} {(z-z_{1})^{2}},$  
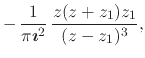$\displaystyle w_{\delta^{2\prime}}(z,z_{1})$ $\textstyle =$ $\displaystyle -\, \frac{1}{\pi\mbox{\boldmath$\imath$}^{2}}\, \frac {z(z+z_{1})z_{1}} {(z-z_{1})^{3}},$  
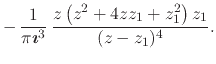$\displaystyle w_{\delta^{3\prime}}(z,z_{1})$ $\textstyle =$ $\displaystyle -\, \frac{1}{\pi\mbox{\boldmath$\imath$}^{3}}\, \frac {z\left(z^{2}+4zz_{1}+z_{1}^{2}\right)z_{1}} {(z-z_{1})^{4}}.$ (60)

These proper inner analytic functions are all very simple rational functions of the complex variable $z$, which can be written as functions of only $z/z_{1}$, and hence as functions of only $\rho$ and $\theta-\theta_{1}$. Note that we can induce from these examples that the $n^{\rm th}$ derivative of the delta ``function'' is indeed represented by an inner analytic function with a pole of order $n+1$ on the unit circle, which is thus a hard singularity with degree of hardness $n+1$, as one would expect from the structure of the corresponding integral-differential chain.

next up previous
Next: Piecewise Polynomial Functions Up: Complex Analysis of Real Previous: The Dirac Delta ``Function''