Next: Derivatives of the Delta Up: Complex Analysis of Real Previous: Synopsis:
This is where we begin the discussion of inner analytic functions that
have hard singularities with strictly positive degrees of hardness. Let us
start by simply introducing a certain particular inner analytic function
of ![]() . If
. If ![]() is a point on the unit circle, this function is defined
as a very simple rational function of
is a point on the unit circle, this function is defined
as a very simple rational function of ![]() ,
,
This inner analytic function has a single point of singularity, which is a
simple pole at ![]() . This is a hard singularity with degree of hardness
equal to one. Our objective here is to examine the properties of the real
part
. This is a hard singularity with degree of hardness
equal to one. Our objective here is to examine the properties of the real
part
![]() of this inner analytic function,
of this inner analytic function,
| (5) |
We will prove that in the
![]() limit
limit
![]() can be interpreted as a Schwartz
distribution [#!DTSchwartz!#,#!DTLighthill!#], namely as the singular
object known as the Dirac delta ``function'', which we will denote
by
can be interpreted as a Schwartz
distribution [#!DTSchwartz!#,#!DTLighthill!#], namely as the singular
object known as the Dirac delta ``function'', which we will denote
by
![]() . This object is also known as a generalized real function, since it is not really a real function in
the usual sense of the term. In the Schwartz theory of distributions this
object plays the role of an integration kernel for a certain distribution.
Note that
. This object is also known as a generalized real function, since it is not really a real function in
the usual sense of the term. In the Schwartz theory of distributions this
object plays the role of an integration kernel for a certain distribution.
Note that
![]() can, in fact, be written explicitly as a
function of
can, in fact, be written explicitly as a
function of ![]() and
and
![]() . Since we have that
. Since we have that
![]() and that
and that
![]() , we have at
once that
, we have at
once that
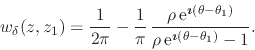 |
(6) |
The definition of the Dirac delta ``function'' is that it is a symbol for
a limiting process, which satisfies certain conditions. In our case here
the limiting process will be the limit
![]() from the open
unit disk to the unit circle. The limit of
from the open
unit disk to the unit circle. The limit of
![]() represents the delta ``function'' in
the sense that it satisfies the conditions that follow.
represents the delta ``function'' in
the sense that it satisfies the conditions that follow.
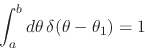 |
(7) |
has the value shown, for any open interval ![]() which contains the
point
which contains the
point ![]() .
.
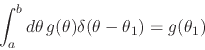 |
(8) |
has the value shown, for any open interval ![]() which contains the
point
which contains the
point ![]() .
.
This is the usual form of this condition, when it is formulated in
strictly real terms. However, we will impose a slight additional
restriction on the real functions ![]() , by assuming that the
limit to the point
, by assuming that the
limit to the point ![]() on the unit circle that corresponds to
on the unit circle that corresponds to
![]() , of the corresponding inner analytic function
, of the corresponding inner analytic function
![]() , exists and is finite. This implies that
, exists and is finite. This implies that ![]() may have at
may have at ![]() a soft singularity, but not a hard singularity.
a soft singularity, but not a hard singularity.
Note that, although it is customary to list both separately, the third condition is in fact just a particular case of the fourth condition. It is also arguable that the second condition is not really necessary, because it is a consequence of the others. We may therefore consider that the only really essential conditions are the first and the fourth ones.
The functions ![]() are sometimes named test functions within
the Schwartz theory of distributions [#!DTSchwartz!#,#!DTLighthill!#]. The
additional part of the fourth condition, that the limit to the point
are sometimes named test functions within
the Schwartz theory of distributions [#!DTSchwartz!#,#!DTLighthill!#]. The
additional part of the fourth condition, that the limit to the point
![]() of the corresponding inner analytic function
of the corresponding inner analytic function ![]() must
exist and be finite, consists of a weak limitation on these test
functions, and does not affect the definition of the singular distribution
itself. This is certainly the case for our definition here, since we
define this object through a definite and unique inner analytic function.
must
exist and be finite, consists of a weak limitation on these test
functions, and does not affect the definition of the singular distribution
itself. This is certainly the case for our definition here, since we
define this object through a definite and unique inner analytic function.
In this section we will prove the following theorem.
Before we attempt to prove this theorem, our first task is to write
explicitly the real and imaginary parts of
![]() . In order
to do this we must now rationalize it,
. In order
to do this we must now rationalize it,
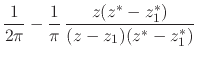 |
|||
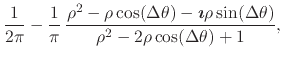 |
(9) |
where
![]() . We must examine the real part of
this function,
. We must examine the real part of
this function,
| (10) |
We are now ready to prove the theorem, which we will do by simply verifying all the properties of the Dirac delta ``function''.
If we take the limit
![]() , under the assumption that
, under the assumption that
![]() , we get
, we get
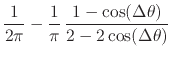 |
|||
| (11) |
which is the correct value for the case of the Dirac delta ``function''. Thus we see that the first condition is satisfied.
If, on the other hand, we calculate
![]() for
for
![]() and
and ![]() we obtain
we obtain
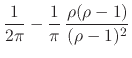 |
|||
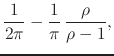 |
(12) |
which diverges to positive infinity as
![]() , as it should in
order to represent the singular Dirac delta ``function''. This establishes
that the second condition is satisfied.
, as it should in
order to represent the singular Dirac delta ``function''. This establishes
that the second condition is satisfied.
We now calculate the real integral of
![]() over the circle of radius
over the circle of radius ![]() , which is given by
, which is given by
since
![]() . This real integral over
. This real integral over ![]() can be calculated by residues. We introduce an auxiliary complex variable
can be calculated by residues. We introduce an auxiliary complex variable
![]() , which becomes simply
, which becomes simply
![]() on the unit circle
on the unit circle ![]() . We have
. We have
![]() , and so we may write the integral on the
right-hand side as
, and so we may write the integral on the
right-hand side as
![$\displaystyle \int_{-\pi}^{\pi}d(\Delta\theta)\,
\frac{1}{\left[\left(1+\rho^{2}\right)/(2\rho)\right]-\cos(\Delta\theta)}$](img59.png) |
![$\displaystyle \oint_{C}d\xi\,
\frac{1}{\mbox{\boldmath$\imath$}\xi}\,
\frac{2}{\left[\left(1+\rho^{2}\right)/\rho\right]-\xi-1/\xi}$](img60.png) |
||
![$\displaystyle 2\mbox{\boldmath$\imath$}
\oint_{C}d\xi\,
\frac{1}{1-\left[\left(1+\rho^{2}\right)/\rho\right]\xi+\xi^{2}},$](img61.png) |
(14) |
where the integral is now over the unit circle ![]() in the complex
in the complex ![]() plane. The two roots of the quadratic polynomial on
plane. The two roots of the quadratic polynomial on ![]() in the
denominator are given by
in the
denominator are given by
| (15) |
Since ![]() , only the simple pole corresponding to
, only the simple pole corresponding to ![]() lies
inside the integration contour, so we get for the integral
lies
inside the integration contour, so we get for the integral
![$\displaystyle \int_{-\pi}^{\pi}d\theta\,
\frac{1}{\left[\left(1+\rho^{2}\right)/(2\rho)\right]-\cos(\Delta\theta)}$](img69.png) |
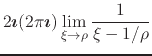 |
||
| (16) |
It follows that we have for the real integral in Equation (13)
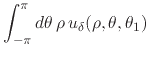 |
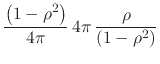 |
||
| (17) |
and thus we have that the integral is equal to ![]() in the
in the
![]() limit. Once we have this result, and since according to the first
condition the integrand goes to zero everywhere on the unit circle except
at
limit. Once we have this result, and since according to the first
condition the integrand goes to zero everywhere on the unit circle except
at
![]() , which is the same as
, which is the same as
![]() , the
integral can be changed to one over any open interval
, the
integral can be changed to one over any open interval ![]() on the unit
circle containing the point
on the unit
circle containing the point ![]() , without any change in its
limiting value. This establishes that the third condition is satisfied.
, without any change in its
limiting value. This establishes that the third condition is satisfied.
In order to establish the validity of the fourth and last condition, we
consider an essentially arbitrary integrable real function ![]() ,
with the additional restriction that it be continuous at the point
,
with the additional restriction that it be continuous at the point
![]() . As was established in [#!CAoRFI!#], it corresponds to an inner
analytic function
. As was established in [#!CAoRFI!#], it corresponds to an inner
analytic function
| (18) |
where we also assume that ![]() is such that
is such that ![]() may
have at
may
have at ![]() a soft singularity, but not a hard singularity, so that
its limit to
a soft singularity, but not a hard singularity, so that
its limit to ![]() exists. We now consider the following real
integral2 over the circle of radius
exists. We now consider the following real
integral2 over the circle of radius ![]() ,
,
since
![]() . This real integral over
. This real integral over ![]() can be calculated by residues, exactly like the one in
Equation (13) which appeared before in the case of the third
condition. The calculation is exactly the same except for the extra factor
of
can be calculated by residues, exactly like the one in
Equation (13) which appeared before in the case of the third
condition. The calculation is exactly the same except for the extra factor
of
![]() to be taken into consideration when
calculating the residue, so that we may write directly that
to be taken into consideration when
calculating the residue, so that we may write directly that
![$\displaystyle \int_{-\pi}^{\pi}d(\Delta\theta)\,
\frac
{u_{\gamma}(\rho,\theta)}
{\left[\left(\rho^{2}+1\right)/(2\rho)\right]-\cos(\Delta\theta)}$](img81.png) |
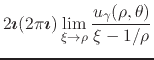 |
||
| (20) |
Note now that since
![]() , and since we must
take the limit
, and since we must
take the limit ![]() , we in fact have that in that limit
, we in fact have that in that limit
| (21) |
which implies that ![]() and that
and that
![]() , and therefore
that
, and therefore
that
![]() . We must therefore write
. We must therefore write
![]() at the point given by
at the point given by ![]() and
and ![]() ,
thus obtaining
,
thus obtaining
| (22) |
It follows that we have for the real integral in Equation (19)
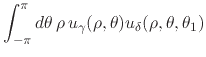 |
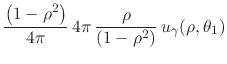 |
||
| (23) |
Finally, we may now take the
![]() limit, since
limit, since
![]() and thus
and thus
![]() are well defined at
are well defined at
![]() in that limit, and thus obtain
in that limit, and thus obtain
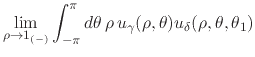 |
|||
![$\displaystyle \int_{-\pi}^{\pi}d\theta\,
u_{\gamma}(1,\theta)
\left[
\lim_{\rho\to 1_{(-)}}
u_{\delta}(\rho,\theta,\theta_{1})
\right]$](img92.png) |
|||
![$\displaystyle \int_{-\pi}^{\pi}d\theta\,
g(\theta)
\left[
\lim_{\rho\to 1_{(-)}}
u_{\delta}(\rho,\theta,\theta_{1})
\right]$](img93.png) |
(24) |
since
![]() converges to
converges to ![]() , in the
, in the
![]() limit, almost everywhere on the unit circle. Just as before, once
we have this result, and since according to the first condition the
integrand goes to zero everywhere on the unit circle except at
limit, almost everywhere on the unit circle. Just as before, once
we have this result, and since according to the first condition the
integrand goes to zero everywhere on the unit circle except at
![]() , which is the same as
, which is the same as
![]() , the integral
can be changed to one over any open interval on the unit circle containing
the point
, the integral
can be changed to one over any open interval on the unit circle containing
the point ![]() , without any change in its value. This establishes
that the fourth and last condition is satisfied.
, without any change in its value. This establishes
that the fourth and last condition is satisfied.
Having established all the properties, we may now write symbolically that
| (25) |
This concludes the proof of Theorem 1.
It is important to note that, when we adopt as the definition of the
Dirac delta ``function'' the
![]() limit of the real part of
the inner analytic function
limit of the real part of
the inner analytic function
![]() , the limitations imposed
on the test functions
, the limitations imposed
on the test functions ![]() and on the corresponding inner analytic
functions
and on the corresponding inner analytic
functions ![]() become irrelevant. In fact, this definitions
stands by itself, and is independent of any set of test functions. Given
any integrable real function
become irrelevant. In fact, this definitions
stands by itself, and is independent of any set of test functions. Given
any integrable real function ![]() and the corresponding inner
analytic function
and the corresponding inner
analytic function ![]() with real part
with real part
![]() , we may always
assemble the real integral over a circle of radius
, we may always
assemble the real integral over a circle of radius ![]()
| (26) |
which is always well defined within the open unit disk. It then
remains to be verified only whether or not the
![]() limit of
this integral exists, in order to define the corresponding integral
limit of
this integral exists, in order to define the corresponding integral
| (27) |
This limit may exist for functions that do not satisfy the conditions
imposed on the test functions. In fact, one can do this for the real part
of any inner analytic function, regardless of whether or not it
corresponds to an integrable inner analytic function, so long as the
![]() limit of
limit of
![]() exists almost everywhere.
Whenever the
exists almost everywhere.
Whenever the
![]() limit of the integral exists, it defines
the action of the delta ``function'' on that particular real object.
limit of the integral exists, it defines
the action of the delta ``function'' on that particular real object.
It is also interesting to observe that the Dirac delta ``function'',
although it is not simply a conventional integrable real function, is in
effect an integrable real object, even if it corresponds to an inner
analytic functions that has a simple pole at ![]() , which is a
non-integrable hard singularity, with degree of hardness equal to
one. This apparent contradiction is explained by the orientation of
the pole at
, which is a
non-integrable hard singularity, with degree of hardness equal to
one. This apparent contradiction is explained by the orientation of
the pole at ![]() . If we consider the real part
. If we consider the real part
![]() of the inner analytic function
of the inner analytic function
![]() , although it is not integrable along curves arriving
at the singular point from most directions, there is one direction, that
of the unit circle, along which one can approach the singular point so
that
, although it is not integrable along curves arriving
at the singular point from most directions, there is one direction, that
of the unit circle, along which one can approach the singular point so
that
![]() is identically zero during the approach,
which allows us to define its integral using the
is identically zero during the approach,
which allows us to define its integral using the
![]() limit3.
The same is not true, for example, for the imaginary part
limit3.
The same is not true, for example, for the imaginary part
![]() of the same inner analytic function, which
generates the Fourier-conjugate function to the delta ``function'', and
that diverges to infinity as
of the same inner analytic function, which
generates the Fourier-conjugate function to the delta ``function'', and
that diverges to infinity as ![]() when one approaches the
singular point along the unit circle, thus generating a non-integrable
real function in the
when one approaches the
singular point along the unit circle, thus generating a non-integrable
real function in the
![]() limit.
limit.
In the development presented in [#!CAoRFI!#] the real functions were
represented by their Fourier coefficients, and the inner analytic
functions by their Taylor coefficients. We can easily do the same here, if
we observe that the inner analytic function
![]() in
Equation (4) is the sum of a geometric series,
in
Equation (4) is the sum of a geometric series,
This power series is the Taylor series of
![]() around the
origin, and therefore it follows that the Taylor coefficients of this
inner analytic function are given by
around the
origin, and therefore it follows that the Taylor coefficients of this
inner analytic function are given by
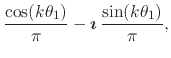 |
(29) |
where
![]() . Since according to the construction
presented in [#!CAoRFI!#] we have that
. Since according to the construction
presented in [#!CAoRFI!#] we have that
![]() and that
and that
![]() , we have for the Fourier coefficients of
the delta ``function''
, we have for the Fourier coefficients of
the delta ``function''
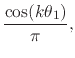 |
|||
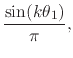 |
(30) |
where
![]() . Note that these are in fact the
results one obtains via the integrals defining the Fourier
coefficients [#!FSchurchill!#],
. Note that these are in fact the
results one obtains via the integrals defining the Fourier
coefficients [#!FSchurchill!#],
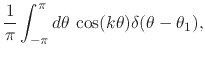 |
|||
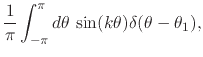 |
(31) |
by simply using the fundamental property of the delta ``function''.
Having established the representation of the Dirac delta ``function''
within the structure of the inner analytic functions, in sequence we will
show that the Dirac delta ``function'' is not the only singular
distribution that can be represented by an inner analytic function. As we
will see, one can do the same for its first derivative, and in fact for
its derivatives of any order. This is an inevitable consequence of the
fact that the proper inner analytic function
![]() associated to
associated to
![]() is a
member of an integral-differential chain.
is a
member of an integral-differential chain.