Next: Products of Distributions Up: Complex Analysis of Real Previous: Derivatives of the Delta
It is important to note that the Dirac delta ``function'' and all its
derivatives, with their singularities located at a given point ![]() on
the unit circle, are all contained within a single integral-differential
chain, making up, in fact, only a part of that chain, the semi-infinite
chain starting from the delta ``function'' and propagating indefinitely in
the differentiation direction along the chain. However, the chain
propagates to infinity in both directions. In order to complete its
analysis, we must now determine what is the character of the real objects
in the remaining part of that chain, in the integration direction. In
fact, they are just integrable real functions, although they do have a
specific character. They consist of sections of polynomials wrapped around
the unit circle, of progressively higher orders, and progressively
smoother across the singular point, as functions of
on
the unit circle, are all contained within a single integral-differential
chain, making up, in fact, only a part of that chain, the semi-infinite
chain starting from the delta ``function'' and propagating indefinitely in
the differentiation direction along the chain. However, the chain
propagates to infinity in both directions. In order to complete its
analysis, we must now determine what is the character of the real objects
in the remaining part of that chain, in the integration direction. In
fact, they are just integrable real functions, although they do have a
specific character. They consist of sections of polynomials wrapped around
the unit circle, of progressively higher orders, and progressively
smoother across the singular point, as functions of ![]() , as one goes
along the integral-differential chain in the integration direction.
, as one goes
along the integral-differential chain in the integration direction.
Let us illustrate this fact with a few simple examples. Instead of
performing angular integrations of the inner analytic functions, we will
do this by performing integrations on the unit circle. As was established
in [#!CAoRFI!#], one can determine these functions by simple integration
on ![]() , so long as one remembers two things: first, to make sure that
the real functions or related objects to be integrated on
, so long as one remembers two things: first, to make sure that
the real functions or related objects to be integrated on ![]() have
zero average over the unit circle, and second, to choose the integration
constant so that the resulting real functions also have zero average over
the unit circle. For example, the integral of the zero-average delta
``function''
have
zero average over the unit circle, and second, to choose the integration
constant so that the resulting real functions also have zero average over
the unit circle. For example, the integral of the zero-average delta
``function''
| (61) |
which is obtained from the real part of the proper inner analytic function in Equation (33), can be integrated by means of the simple use of the fundamental property of the delta ``function'', thus yielding
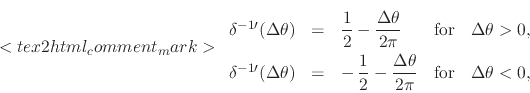 |
where
![]() . This is a sectionally linear
function, with a single section consisting of the intervals
. This is a sectionally linear
function, with a single section consisting of the intervals ![]() and
and
![]() , thus excluding the point
, thus excluding the point
![]() where the singularity
lies, and with a unit-height step discontinuity at that point. Note that
it is an odd function of
where the singularity
lies, and with a unit-height step discontinuity at that point. Note that
it is an odd function of ![]() . The next case can now be
calculated by straightforward integration, which yields
. The next case can now be
calculated by straightforward integration, which yields
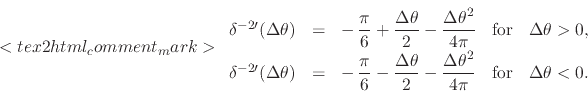 |
This is a sectionally quadratic function, this time a continuous function,
again with the same single section excluding the point
![]() ,
but now with a point of non-differentiability there. Note that it is an
even function of
,
but now with a point of non-differentiability there. Note that it is an
even function of ![]() . The next case yields, once more by
straightforward integration,
. The next case yields, once more by
straightforward integration,
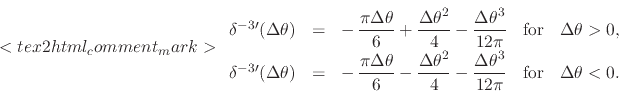 |
This is a sectionally cubic continuous and differentiable function, again
with the same single section excluding the point
![]() . Note
that it is an odd function of
. Note
that it is an odd function of ![]() . The trend is now quite
clear. All the real functions in the chain, in the integration direction
starting from the delta ``function'', are what we may call piecewise
polynomials, even if we have just a single piece within a single
section of the unit circle, as is the case here. The
. The trend is now quite
clear. All the real functions in the chain, in the integration direction
starting from the delta ``function'', are what we may call piecewise
polynomials, even if we have just a single piece within a single
section of the unit circle, as is the case here. The ![]() integral
is a piecewise polynomial of order
integral
is a piecewise polynomial of order ![]() , which has zero average over the
unit circle, and which becomes progressively smoother across the singular
point as one goes along the integral-differential chain in the integration
direction.
, which has zero average over the
unit circle, and which becomes progressively smoother across the singular
point as one goes along the integral-differential chain in the integration
direction.
In order to generalize this analysis, we must now consider linear
superpositions of delta ``functions'' and derivatives of delta
``functions'', with their singularities situated at various points on the
unit circle. A simple example of such a superposition, which we may use to
illustrate what happens when we make one, is that of two delta
``functions'', with singularities at ![]() and at
and at ![]() ,
added together with opposite signs,
,
added together with opposite signs,
| (62) |
that corresponds to the following inner analytic function, which this time
is already a proper inner analytic function, with two simple poles at
![]() ,
,
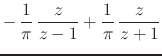 |
|||
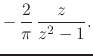 |
(63) |
Since we have now two singular points, one at ![]() and another at
and another at ![]() ,
corresponding respectively to
,
corresponding respectively to ![]() and
and ![]() , we have now
two sections, one in
, we have now
two sections, one in ![]() and another in
and another in ![]() . The inner
analytic functions at the integration side of the integral-differential
chain to which this function belongs are obtained by simply adding the
corresponding inner analytic functions at the integration sides of the
integral-differential chains of the two functions that are superposed. The
same is true for the corresponding real objects within each section of the
unit circle. Since the real functions corresponding to each one of the two
delta ``functions'' that were superposed are zero-average piecewise
polynomials, so are the real functions corresponding to the superposition.
For example, it is not difficult to show that the first integral is the
familiar square wave, with amplitude
. The inner
analytic functions at the integration side of the integral-differential
chain to which this function belongs are obtained by simply adding the
corresponding inner analytic functions at the integration sides of the
integral-differential chains of the two functions that are superposed. The
same is true for the corresponding real objects within each section of the
unit circle. Since the real functions corresponding to each one of the two
delta ``functions'' that were superposed are zero-average piecewise
polynomials, so are the real functions corresponding to the superposition.
For example, it is not difficult to show that the first integral is the
familiar square wave, with amplitude ![]() ,
,
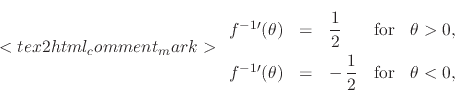 |
which is a piecewise linear function with two sections, having unit-height
step discontinuities with opposite signs at the two singular points
![]() and
and ![]() .
.
We want to determine what is the character of the real functions, in the
integration side of the resulting integral-differential chain, in the most
general case, when we consider arbitrary linear superpositions of a finite
number of delta ``functions'' and derivatives of delta ``functions'', with
their singularities situated at various points on the unit circle. From
the examples we see that, when we superpose several singular distributions
with their singularities at various points, the complete set of all the
singular points defines a new set of sections. Given one of these singular
points, since at least one of the distributions being superposed is
singular at that point, in general so is the superposition. Let there be
![]() singular points
singular points
![]() in the
superposition. It follows that in general we end up with a set of
in the
superposition. It follows that in general we end up with a set of ![]() contiguous sections, consisting of open intervals between singular points,
that can be represented as the sequence
contiguous sections, consisting of open intervals between singular points,
that can be represented as the sequence
| (64) |
where we see that the sequence goes around the unit circle, and where we
adopt the convention that each section
![]() is
numbered after the singular point
is
numbered after the singular point ![]() at its left end. In
addition to this, since for each one of the distributions being superposed
the real functions on the integration side of the integral-differential
chain of the corresponding delta ``function'' are piecewise polynomials,
and since the sum of any finite number of polynomials is also a
polynomial, so are the real functions of the integral-differential chain
to which the superposition belongs, if we are at a point in that
integral-differential chain where all singular distributions have already
been integrated out. Let us establish a general notation for these
piecewise polynomial real functions, as well as a formal definition for
them.
at its left end. In
addition to this, since for each one of the distributions being superposed
the real functions on the integration side of the integral-differential
chain of the corresponding delta ``function'' are piecewise polynomials,
and since the sum of any finite number of polynomials is also a
polynomial, so are the real functions of the integral-differential chain
to which the superposition belongs, if we are at a point in that
integral-differential chain where all singular distributions have already
been integrated out. Let us establish a general notation for these
piecewise polynomial real functions, as well as a formal definition for
them.
Given a real function
![]() that is defined in a piecewise
fashion by polynomials in
that is defined in a piecewise
fashion by polynomials in ![]() sections of the unit circle, with the
exclusion of a finite set of
sections of the unit circle, with the
exclusion of a finite set of ![]() singular points
singular points ![]() , with
, with
![]() , so that the polynomial
, so that the polynomial
![]() at
the
at
the ![]() section has order
section has order ![]() , we denote the function by
, we denote the function by
| (65) |
where ![]() is the largest order among all the
is the largest order among all the ![]() orders
orders ![]() . We say
that
. We say
that
![]() is a piecewise polynomial real function of
order
is a piecewise polynomial real function of
order ![]() .
.
Note that, being made out of finite sections of polynomials, the real
function
![]() is always an integrable real function. In fact,
it is also analytic within each section, so that the
is always an integrable real function. In fact,
it is also analytic within each section, so that the ![]() singularities
described above are the only singularities involved. Since
singularities
described above are the only singularities involved. Since
![]() is an integrable real function, let
is an integrable real function, let ![]() be the inner
analytic function that corresponds to this integrable real function, as
constructed in [#!CAoRFI!#]. The
be the inner
analytic function that corresponds to this integrable real function, as
constructed in [#!CAoRFI!#]. The
![]() angular derivative of
angular derivative of
![]() is the inner analytic function
is the inner analytic function
![]() , which
corresponds therefore to the
, which
corresponds therefore to the
![]() derivative of
derivative of
![]() with respect to
with respect to ![]() , that we denote by
, that we denote by
![]() .
.
In this section we will prove the following theorem.
In order to prove this, first let us note that the derivative
![]() is identically zero within all the open
intervals defining the sections. This is so because the maximum order of
all the polynomials involved is
is identically zero within all the open
intervals defining the sections. This is so because the maximum order of
all the polynomials involved is ![]() , and the
, and the
![]() derivative
of a polynomial of order equal to or less than
derivative
of a polynomial of order equal to or less than ![]() is identically zero,
is identically zero,
| (66) |
We conclude, therefore, that the real object represented by the inner
analytic function
![]() has support only at the
has support only at the ![]() isolated
singular points
isolated
singular points ![]() , thus implying that it can contain only
singular distributions.
, thus implying that it can contain only
singular distributions.
Second, let us prove that the derivative cannot be identically zero over
the whole unit circle. In order to do this we note that one cannot have a
non-zero piecewise polynomial real function of order ![]() , such as the one
described above, that is also continuous and differentiable to the order
, such as the one
described above, that is also continuous and differentiable to the order
![]() on the whole unit circle. This is so because this hypothesis would
lead to an impossible integral-differential chain.
on the whole unit circle. This is so because this hypothesis would
lead to an impossible integral-differential chain.
If this were possible, then starting from a non-zero real function
![]() that corresponds to a non-zero inner analytic function
that corresponds to a non-zero inner analytic function
![]() , and after a finite number
, and after a finite number ![]() of steps along the differentiation
direction of the corresponding integral-differential chain, one would
arrive at a real function that is continuous over the whole unit
circle, that is constant within each section and that has zero
average over the whole unit circle. It follows that such a function
would have to be identically zero, thus corresponding to the inner
analytic function
of steps along the differentiation
direction of the corresponding integral-differential chain, one would
arrive at a real function that is continuous over the whole unit
circle, that is constant within each section and that has zero
average over the whole unit circle. It follows that such a function
would have to be identically zero, thus corresponding to the inner
analytic function ![]() . But this is not possible, because this
inner analytic function belongs to another chain, the one which is
constant, all members being
. But this is not possible, because this
inner analytic function belongs to another chain, the one which is
constant, all members being ![]() , and we have shown
in [#!CAoRFI!#] that two different integral-differential chains cannot
intersect.
, and we have shown
in [#!CAoRFI!#] that two different integral-differential chains cannot
intersect.
It follows that
![]() can be globally differentiable at most
to order
can be globally differentiable at most
to order ![]() , so that the
, so that the ![]() derivative is a discontinuous
function, and therefore the
derivative is a discontinuous
function, and therefore the
![]() derivative already gives rise
to singular distributions. Therefore, every real function that is
piecewise polynomial on the unit circle, of order
derivative already gives rise
to singular distributions. Therefore, every real function that is
piecewise polynomial on the unit circle, of order ![]() , when differentiated
, when differentiated
![]() times, so that it becomes zero within the open intervals
corresponding to the existing sections, will always result in the
superposition of some non-empty set of singular distributions with their
singularities located at the points between two consecutive sections.
times, so that it becomes zero within the open intervals
corresponding to the existing sections, will always result in the
superposition of some non-empty set of singular distributions with their
singularities located at the points between two consecutive sections.
We can also establish that only functions of this form give rise to
such superpositions of singular distributions and of nothing else. The
necessity of the fact that the real functions on integral-differential
chains generated by superpositions of singular distributions must be
piecewise polynomials comes directly from the fact that all such
distributions and all such superpositions of distributions are zero almost
everywhere, in fact everywhere but at their singular points. Due to this,
it is necessary that these real functions, upon a finite number
![]() of differentiations, become zero everywhere strictly within the
sections, that is, within the open intervals between two successive
singularities. Therefore, within each open interval the condition over the
sectional real function at that interval is that
of differentiations, become zero everywhere strictly within the
sections, that is, within the open intervals between two successive
singularities. Therefore, within each open interval the condition over the
sectional real function at that interval is that
| (67) |
and the general solution of this ordinary differential equation of order
![]() is a polynomial of order
is a polynomial of order ![]() , containing at most
, containing at most ![]() non-zero arbitrary constants,
non-zero arbitrary constants,
| (68) |
Since only polynomials have the property of becoming identically zero after a finite number of differentiations, it is therefore an absolute necessity that these real functions be polynomials within each one of the sections. This completes the proof of Theorem 3.
Note that the inner analytic function
![]() corresponding to
corresponding to
![]() represents therefore the superposition of
a non-empty set of singular distributions with their singularities located
at the singular points. In other words, after
represents therefore the superposition of
a non-empty set of singular distributions with their singularities located
at the singular points. In other words, after ![]() angular
differentiations of
angular
differentiations of ![]() , which correspond to
, which correspond to ![]() straight
differentiations with respect to
straight
differentiations with respect to ![]() of the polynomials
of the polynomials
![]() within the sections, one is left with an inner
analytic function
within the sections, one is left with an inner
analytic function
![]() whose real part converges to zero in
the
whose real part converges to zero in
the
![]() limit, at all points on the unit circle which are
not one of the
limit, at all points on the unit circle which are
not one of the ![]() singular points.
singular points.
It is interesting to note that, since we have the inner analytic function that corresponds to the Dirac delta ``function'' in explicit form, it is not difficult to calculate directly its first angular primitive. A few simple and straightforward calculations lead to
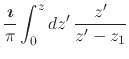 |
|||
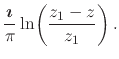 |
(69) |
This inner analytic function has a logarithmic singularity at ![]() ,
which is a borderline hard singularity. Note that, as expected, we have
that
,
which is a borderline hard singularity. Note that, as expected, we have
that
![]() .
.