Behavior Under Analytic Operations

Let us now discuss how the correspondence between inner analytic functions and integrable real functions behaves under the respective operations of differentiation and integration, that take us along the corresponding integral-differential chain. There are two issues here, one being the existence of the $\rho\to 1_{(-)}$ limit at each point on the unit circle, the other being whether or not the correspondence between the real function $f(\theta)$ and the inner analytic function $w(z)$, established by the construction of the inner analytic function from the integrable real function, and by the $\rho\to 1_{(-)}$ limit of the real part of the inner analytic function, survives the operation unscathed.

The existence of the limit $\rho\to 1_{(-)}$ hinges on whether the point at issue is a singular point or not, and then on whether the singularity at the point is either soft or hard. If a point on the unit circle is not a singularity of the inner analytic function $w(z)$, then the $\rho\to 1_{(-)}$ limit always exists at that point, no matter how many angular integrations or angular differentiations are performed on the inner analytic function, that is, the limit exists throughout the corresponding integral-differential chain. The same is true if the point is an infinitely soft singularity of $w(z)$. On the other hand, if it is an infinitely hard singularity of $w(z)$, then the limit at that point never exists, in the complex sense, throughout the integral-differential chain. Note, however, that in some cases the limit may still exist, in the real sense, along the unit circle.

If the point on the unit circle is a soft singularity of $w(z)$ with a finite degree of softness $n_{s}$, then the $\rho\to 1_{(-)}$ limit exists no matter how many angular integrations are performed, since the operation of angular integration takes soft singularities to other soft singularities. However, since the operation of angular differentiation may take soft singularities to hard singularities, the limit will only exist up to a certain number of angular differentiations, which is given by $n_{s}-1$. Again, we note that in some cases the limit may still exist beyond this point, in the real sense, even if it does not exist in the complex sense.

If the point on the unit circle is a hard singularity of $w(z)$ with a finite degree of hardness $n_{h}$, including zero, then the $\rho\to 1_{(-)}$ limit does not exist in the complex sense, and will also fail to exist in that sense for any of the angular derivatives of $w(z)$, since the operation of angular differentiation takes hard singularities to other hard singularities. Once more we note that in some cases the limit may still exist in the real sense, even if it does not exist in the complex sense. However, since the operation of angular integration may take hard singularities to soft singularities, the limit will in fact exist after a certain number of angular integrations of $w(z)$, which is given by $n_{h}+1$.

Whatever the situation may be, if after a given set of analytic operations is performed there is at most a finite number of hard singularities, then the $\rho\to 1_{(-)}$ limit exists almost everywhere, and therefore the corresponding real function can be recovered at almost all points on the unit circle. Note, by the way, that the same is true if there is a denumerably infinite number of hard singularities, so long as they are not densely distributed on the unit circle or any part of it, so that almost all of then can be isolated.

The next question is whether or not the relation between the real function $f(\theta)$ and the inner analytic function $w(z)$ implies the corresponding relation between the corresponding functions after an operation of integration or differentiation is applied. This is always true from a strictly local point of view, since we have shown in Section 2 that the operation of angular differentiation on the open unit disk reduces to the operation of differentiation with respect to $\theta$ on the unit circle, and that the operation of angular integration on the open unit disk reduces to the operation of integration with respect to $\theta$ on the unit circle, up to an integration constant.

There are, however, some global concerns over the unit circle, since the operations of angular integration and of angular differentiation always result in proper inner analytic functions, and there is no corresponding property of the operations of integration and differentiation with respect to $\theta$ on the unit circle. Note that the condition $w(0)=0$, which holds for a proper inner analytic function, is translated, on the unit circle, to the global condition that the corresponding real function $f(\theta)$ have zero average value over that unit circle. This is so because $w(0)=0$ is equivalent to $c_{0}=0$, and therefore to $\alpha_{0}=0$. However, according to the definition of the Fourier coefficients in Equation (20), the coefficient $\alpha_{0}/2$ is equal to that average value.

One way to examine this issue is to use the correspondence between the Taylor coefficients $c_{k}$ of the inner analytic function $w(z)$ and the Fourier coefficients $\alpha_{k}$ and $\beta_{k}$ of the integrable real function $f(\theta)$, which according to our construction of $w(z)$ are related by the relations in Equation (24). Since we have that

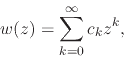$$w(z) = \sum_{k=0}^{\infty} c_{k}z^{k},$$ (52)

it follows from the definition of angular differentiation that under that operation the coefficients $c_{k}$ transform as

$$c_{0} \rightarrow 0,$$

$$c_{k} \rightarrow \mbox{\boldmath$\imath$}k c_{k},$$ (53)

for $k\in\{1,2,3,\ldots,\infty\}$, and it also follows that from the definition of angular integration that under that operation they transform as

$$c_{0} \rightarrow 0,$$

$$c_{k} \rightarrow -\, \frac{\mbox{\boldmath$\imath$}}{k}\, c_{k},$$ (54)

for $k\in\{1,2,3,\ldots,\infty\}$. If we now look at the Fourier coefficients, considering their definition in Equation (20), in the case $k=0$ we have that under differentiation $\alpha_{0}$ transforms as

$$\alpha_{0} \rightarrow \frac{1}{\pi} \int_{-\pi}^{\pi}d\theta\, f'(\theta)$$

$$= \frac{1}{\pi} \int_{-\pi}^{\pi}df(\theta),$$ (55)

which is zero so long as $f(\theta)$ is a continuous function, since we are integrating on a circle. Note that, if $f(\theta)$ is not continuous, then $f'(\theta)$ is not even a well defined integrable real function, and we therefore cannot even write the integral, with what we know so far. In the case $k>0$ we have that under differentiation the Fourier coefficients transform as

$$\alpha_{k} \rightarrow \frac{1}{\pi} \int_{-\pi}^{\pi}d\theta\, f'(\theta)\cos(k\theta)$$

$$= \frac{k}{\pi} \int_{-\pi}^{\pi}d\theta\, f(\theta)\sin(k\theta)$$

$$= k\beta_{k},$$

$$\beta_{k} \rightarrow \frac{1}{\pi} \int_{-\pi}^{\pi}d\theta\, f'(\theta)\sin(k\theta)$$

$$= -\, \frac{k}{\pi} \int_{-\pi}^{\pi}d\theta\, f(\theta)\cos(k\theta)$$

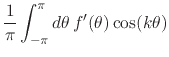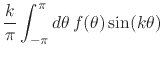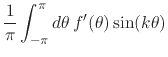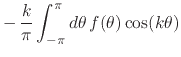$$= -k\alpha_{k},$$ (56)

where we have integrated by parts, noting that the integrated terms are zero because we are integrating on a circle. We therefore have, so long as $f(\theta)$ is a continuous function, that

$$\alpha_{0} \rightarrow 0,$$

$$\alpha_{k}-\mbox{\boldmath$\imath$}\beta_{k} \rightarrow \mbox{\boldmath$\imath$}k \left( \alpha_{k} - \mbox{\boldmath$\imath$} \beta_{k} \right),$$ (57)

for $k\in\{1,2,3,\ldots,\infty\}$, which are, therefore, the same transformations undergone by $c_{k}$. In the case of integration operations the change in $\alpha_{0}$ is indeterminate due to the presence of an arbitrary integration constant on $\theta$ and, considering once more the definition of the Fourier coefficients in Equation (20), we have that for $k>0$ the Fourier coefficients transform under integration as

$$\alpha_{k} \rightarrow \frac{1}{\pi} \int_{-\pi}^{\pi}d\theta\, f^{-1\prime}(\theta)\cos(k\theta)$$

$$= -\, \frac{1}{k\pi} \int_{-\pi}^{\pi}d\theta\, f(\theta)\sin(k\theta)$$

$$= -\, \frac{\beta_{k}}{k},$$

$$\beta_{k} \rightarrow \frac{1}{\pi} \int_{-\pi}^{\pi}d\theta\, f^{-1\prime}(\theta)\sin(k\theta)$$

$$= \frac{1}{k\pi} \int_{-\pi}^{\pi}d\theta\, f(\theta)\cos(k\theta)$$

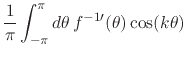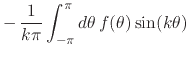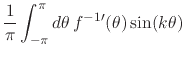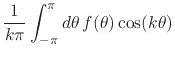$$= \frac{\alpha_{k}}{k},$$ (58)

where we have again integrated by parts, noting once more that the integrated terms are zero because we are integrating on a circle. We therefore have, so long as $f(\theta)$ is an integrable function, and so long as one chooses the integration constant of the integration on $\theta$ leading to $f^{-1\prime}(\theta)$ so that $\alpha_{0}$ is mapped to zero, that

$$\alpha_{0} \rightarrow 0,$$

$$\alpha_{k}-\mbox{\boldmath$\imath$}\beta_{k} \rightarrow -\, \frac{\mbox{\boldmath$\imath$}}{k} \left( \alpha_{k} - \mbox{\boldmath$\imath$} \beta_{k} \right),$$ (59)

for $k\in\{1,2,3,\ldots,\infty\}$, which are, once more, the same transformations undergone by $c_{k}$. We therefore see that, from the point of view of the respective coefficients, the correspondence between the real function $f(\theta)$ and the inner analytic function $w(z)$ survives the respective analytic operations, so long as the operations produce integrable real functions on the unit circle, and so long as one chooses appropriately the integration constant on $\theta$.

Let us discuss the situation in a little more detail, starting with the operation of integration. As we saw in Property 3.1 of Section 2, angular integration is translated, up to an integration constant, to integration with respect to $\theta$ on the unit circle, when we take the $\rho\to 1_{(-)}$ limit. In addition to this, angular integration never produces new hard singularities out of soft ones, so that the $\rho\to 1_{(-)}$ limit giving $f^{-1\prime}(\theta)$ exists at all points where those giving $f(\theta)$ exist. We see therefore that, so long as the integration constant is chosen so as to satisfy the condition that the function $f^{-1\prime}(\theta)$ have zero average value over the unit circle, it follows that the correspondence between the real function $f(\theta)$ and the inner analytic function $w(z)$ implies the correspondence between the real function $f^{-1\prime}(\theta)$ and the inner analytic function $w(z)^{-1\mbox{\Large$\cdot$}\!}$,

$$f(\theta) \longleftrightarrow w(z) \;\;\;\Rightarrow$$

$$f^{-1\prime}(\theta) \longleftrightarrow w^{-1\mbox{\Large$\cdot$}\!}(z).$$ (60)

This is valid so long as $f(\theta)$ is an integrable real function. Let us now discuss the case of the operation of differentiation. As we saw in Property 2.1 of Section 2, angular differentiation corresponds to differentiation with respect to $\theta$ on the unit circle, when we take the $\rho\to 1_{(-)}$ limit. However, angular differentiation can produce new hard singularities out of soft ones, and can also produce non-integrable hard singularities out of borderline hard ones. Therefore, we may conclude only that, if all the singularities of $w(z)$ are soft, which implies that $f(\theta)$ is continuous, then the correspondence between the real function $f(\theta)$ and the inner analytic function $w(z)$ does imply the correspondence between the real function $f'(\theta)$ and the inner analytic function $w^{\mbox{\Large$\cdot$}\!}(z)$,

$$f(\theta) \longleftrightarrow w(z) \;\;\;\Rightarrow$$

$$f'(\theta) \longleftrightarrow w^{\mbox{\Large$\cdot$}\!}(z),$$ (61)

with the exception of the points where $f'(\theta)$ has hard singularities produced out of soft singularities of $f(\theta)$. Note, however, that this statement is true even if $w^{\mbox{\Large$\cdot$}\!}(z)$ has borderline hard singularities and therefore $f'(\theta)$ is not continuous.

On the other hand, if $f(\theta)$ is discontinuous at a finite set of borderline hard singularities of $w(z)$, then $f'(\theta)$ is not even well defined everywhere, by the usual definition of the derivative of a real function. In fact, if $w(z)$ has borderline hard singularities then $w^{\mbox{\Large$\cdot$}\!}(z)$ has hard singularities with degrees of hardness equal to one, which are non-integrable singularities, so that $f'(\theta)$ is not necessarily an integrable real function. The same is true if the inner analytic function $w(z)$ has hard singularities with strictly positive degrees of hardness. The discussion of cases such as these will be given in the aforementioned forthcoming papers.

Given any inner analytic function that has at most a finite number of borderline hard singular points and no singularities harder than that, and the corresponding integral-differential chain, the results obtained here allow us to travel freely along the integration side of the chain, without damaging the correspondence between each inner analytic function and the corresponding real function. The part of the chain where this is valid is the part to the integration side starting from the link where all the singularities are either soft or at most borderline hard. What happens when one travels in the other direction along the chain, starting from this link, will be discussed in the aforementioned forthcoming papers.