Next: Representation of Integrable Real Up: Complex Analysis of Real Previous: Introduction
Here we will introduce the definitions and basic properties of some objects and structures which are not usually discussed in complex analysis [#!CVchurchill!#], and which we will use in the subsequent sections. Consider then the unit circle centered at the origin of the complex plane. Its interior is the open unit disk we will often refer to along the paper. Any reference to the unit disk or to the unit circle should always be understood to refer to those centered at the origin.
A complex function ![]() which is analytic in the open unit disk will be
named an inner analytic function. We will consider the set of all
such functions. We will also consider the subset of such functions that
have the additional property that
which is analytic in the open unit disk will be
named an inner analytic function. We will consider the set of all
such functions. We will also consider the subset of such functions that
have the additional property that ![]() , which we will name proper
inner analytic functions.
, which we will name proper
inner analytic functions.
Note, in passing, that the set of all inner analytic functions forms a vector space over the field of complex numbers, and so does the subset of all proper inner analytic functions.
The focus of this study will be the set of real objects which are obtained
from the real parts of these inner analytic functions when we take the
limit from the open unit disk to its boundary, that is, to the unit
circle. Specifically, if we describe the complex plane with polar
coordinates ![]() , then an arbitrary inner analytic function can
be written as
, then an arbitrary inner analytic function can
be written as
| (1) |
where
![]() is the imaginary unit, and we consider the set of real objects
is the imaginary unit, and we consider the set of real objects
![]() obtained from the set of all inner analytic functions as the
limits of their real parts, from the open unit disk to the unit circle,
obtained from the set of all inner analytic functions as the
limits of their real parts, from the open unit disk to the unit circle,
| (2) |
when and where such limits exist, or at least can be defined in a consistent way.
Note that an inner analytic function may have any number of singularities on the unit circle, as well as in the region outside the unit circle. The concept of a singularity is the usual one in complex analysis, namely that a singular point is simply a point where the function fails to be analytic. The singularities on the unit circle will play a particularly important role in the complex-analytic structure to be presented in this paper. If any of these singularities turn out to be branch points, then we assume that the corresponding branch cuts extend outward from the unit circle, either out to infinity or connecting to some other singularity that may exist outside the open unit disk.
Note also that the imaginary parts of the inner analytic functions do not generate an independent set of real objects, since the imaginary
part
![]() of the inner analytic function
of the inner analytic function ![]() is also the
real part of the inner analytic function
is also the
real part of the inner analytic function ![]() given by
given by
| (3) |
We thus see, however, that the inner analytic functions do organize the
real functions in matched pairs, those originating from the real and
imaginary parts of each inner analytic function. The two real functions
forming such a pair may be described as mutually Fourier conjugate
functions. Finally, we will assume that, at all singular points where the
functions ![]() can still be defined by continuity, they have been so
defined.
can still be defined by continuity, they have been so
defined.
In addition to establishing this correspondence between complex functions on the unit disk and real function of the unit circle, we will find it necessary to define analytic operations on the complex functions that correspond to the ordinary operations of differentiation and integration on the real functions. As will be shown in what follows, the next two definitions accomplish this.
Given an arbitrary inner analytic function ![]() , its angular
derivative is defined by
, its angular
derivative is defined by
| (4) |
The angular derivative of ![]() will be denoted by the shifted dot, as
shown. The second angular derivative will be denoted by
will be denoted by the shifted dot, as
shown. The second angular derivative will be denoted by
![]() ,
and so on.
,
and so on.
Note that this definition has been tailored in order for the following property to hold.
Writing
![]() , and considering the partial derivative of
, and considering the partial derivative of
![]() with respect to
with respect to ![]() , we have
, we have
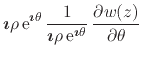 |
|||
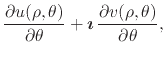 |
(5) |
which establishes this property.
Note that by construction we always have that
![]() , so that we
may say that the operation of angular differentiation projects the space
of inner analytic functions onto the space of proper inner analytic
functions. We may now prove an important property of the angular
derivative.
, so that we
may say that the operation of angular differentiation projects the space
of inner analytic functions onto the space of proper inner analytic
functions. We may now prove an important property of the angular
derivative.
Let us recall that the derivative of an analytic function always exists
and is also analytic, in the same domain of analyticity of the original
function. Since the constant function
![]() and the identity
function
and the identity
function ![]() are analytic in the whole complex plane, and since
the product of analytic functions is also an analytic function, in their
common domain of analyticity, it follows at once that the angular
derivative of an inner analytic function is an inner analytic function as
well, which establishes this property.
are analytic in the whole complex plane, and since
the product of analytic functions is also an analytic function, in their
common domain of analyticity, it follows at once that the angular
derivative of an inner analytic function is an inner analytic function as
well, which establishes this property.
In other words, the operation of angular differentiation stays within the
space of inner analytic functions. Note that, since
![]() ,
angular differentiation always results in proper inner analytic
functions, and therefore that this operation also stays within the space
of proper inner analytic functions.
,
angular differentiation always results in proper inner analytic
functions, and therefore that this operation also stays within the space
of proper inner analytic functions.
Given an arbitrary inner analytic function ![]() , its angular
primitive is defined by
, its angular
primitive is defined by
where the integral is taken along any simple curve from ![]() to
to ![]() contained within the open unit disk. Since the integrand is analytic
inside the open unit disk, including at the origin, as we will see shortly
while proving Property 3.2, due to the Cauchy-Goursat
theorem the integral does not depend on the curve along which it is taken.
The angular primitive will also be denoted by a shifted dot, this time
preceded by a negative integer, as indicated above.
contained within the open unit disk. Since the integrand is analytic
inside the open unit disk, including at the origin, as we will see shortly
while proving Property 3.2, due to the Cauchy-Goursat
theorem the integral does not depend on the curve along which it is taken.
The angular primitive will also be denoted by a shifted dot, this time
preceded by a negative integer, as indicated above.
Let us prove that the apparent singularity of the integrand at ![]() is in
fact a removable singularity, so that the integrand can be defined at the
origin by continuity, thus producing a function which is continuous and
well defined there. If we simply take the
is in
fact a removable singularity, so that the integrand can be defined at the
origin by continuity, thus producing a function which is continuous and
well defined there. If we simply take the ![]() limit of the integrand
we get
limit of the integrand
we get
| (7) |
since this limit is the very definition of the derivative of ![]() at
at
![]() . Since
. Since ![]() is an inner analytic function, and is thus analytic in
the open unit disk, it is differentiable at the origin, so that this limit
exists and is finite. Therefore the integrand can be defined at the origin
to have this particular value, so that it is continuous there. We assume
that the integrand is so defined at
is an inner analytic function, and is thus analytic in
the open unit disk, it is differentiable at the origin, so that this limit
exists and is finite. Therefore the integrand can be defined at the origin
to have this particular value, so that it is continuous there. We assume
that the integrand is so defined at ![]() , as part of the definition of
the angular primitive.
, as part of the definition of
the angular primitive.
Note that this definition has been tailored in order for the following property to hold.
Given any point ![]() in the open unit disk, and considering that we are
free to choose the path of integration from
in the open unit disk, and considering that we are
free to choose the path of integration from ![]() to
to ![]() , we now choose to
go first from the origin along the positive real axis, until we reach the
radius
, we now choose to
go first from the origin along the positive real axis, until we reach the
radius ![]() , and then to go along an arc of circle of radius
, and then to go along an arc of circle of radius ![]() ,
until we reach the angle
,
until we reach the angle ![]() , thus separating the integral in two. In
the first integral the variations of
, thus separating the integral in two. In
the first integral the variations of ![]() are given by
are given by ![]() , and in
the second one they are given by
, and in
the second one they are given by
![]() . Note
that as the integrand in Equation (6) we have the proper inner analytic function given by
. Note
that as the integrand in Equation (6) we have the proper inner analytic function given by
| (8) |
where ![]() . The integral in Equation (6) can
therefore be written as
. The integral in Equation (6) can
therefore be written as
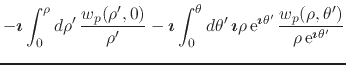 |
|||
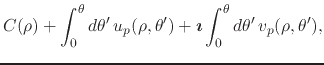 |
(9) |
where, in relation to the variable ![]() , the integral on
, the integral on ![]() becomes the complex function
becomes the complex function ![]() , which depends only on
, which depends only on ![]() and
not on
and
not on ![]() , while the integral on
, while the integral on ![]() determines primitives
with respect to
determines primitives
with respect to ![]() of the real and imaginary parts of
of the real and imaginary parts of ![]() ,
which thus establishes this property.
,
which thus establishes this property.
Note that by construction we always have that
![]() , so that
we may say that the operation of angular integration projects the space of
inner analytic functions onto the space of proper inner analytic
functions. We may now establish an important property of the angular
primitive.
, so that
we may say that the operation of angular integration projects the space of
inner analytic functions onto the space of proper inner analytic
functions. We may now establish an important property of the angular
primitive.
In order to prove that
![]() is an inner analytic function, we
use the power-series representation of the inner analytic function
is an inner analytic function, we
use the power-series representation of the inner analytic function ![]() .
Since this function is analytic within the open unit disk, its Taylor
series around
.
Since this function is analytic within the open unit disk, its Taylor
series around ![]() , which is given by
, which is given by
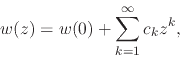 |
(10) |
where
![]() are the Taylor coefficients of
are the Taylor coefficients of ![]() with
respect to the origin and where
with
respect to the origin and where
![]() is the
is the ![]() derivative of
derivative of ![]() , converges within that disk. We therefore have for
the integrand in Equation (6) the power-series representation
, converges within that disk. We therefore have for
the integrand in Equation (6) the power-series representation
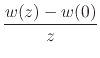 |
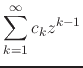 |
||
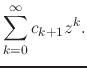 |
(11) |
Since this series has the same set of coefficients as the convergent
series of ![]() , it is equally convergent, as is implied for example by
the ratio test. Note that this shows, in particular, that the integrand is
analytic at
, it is equally convergent, as is implied for example by
the ratio test. Note that this shows, in particular, that the integrand is
analytic at ![]() . Being a convergent power series, this series can be
integrated term by term, resulting in an equally convergent power series,
so that we have for the angular primitive
. Being a convergent power series, this series can be
integrated term by term, resulting in an equally convergent power series,
so that we have for the angular primitive
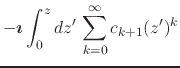 |
|||
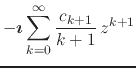 |
|||
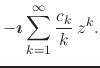 |
(12) |
Due to the factors of ![]() , when
, when ![]() the coefficients of this
series go to zero faster than those of the convergent Taylor series of
the coefficients of this
series go to zero faster than those of the convergent Taylor series of
![]() , and thus it is also convergent, in the same domain of convergence
of the Taylor series of
, and thus it is also convergent, in the same domain of convergence
of the Taylor series of ![]() . This confirms that this series is
convergent within the open unit disk. Being a convergent power series, it
converges to an analytic function, thus proving that
. This confirms that this series is
convergent within the open unit disk. Being a convergent power series, it
converges to an analytic function, thus proving that
![]() is
analytic within the open unit disk. We may conclude therefore that the
angular primitive of an inner analytic function is an inner analytic
function as well, which establishes this property.
is
analytic within the open unit disk. We may conclude therefore that the
angular primitive of an inner analytic function is an inner analytic
function as well, which establishes this property.
In other words, the operation of angular integration stays within the
space of inner analytic functions. Note that, since
![]() ,
angular integration always results in proper inner analytic
functions, and therefore that this operation also stays within the space
of proper inner analytic functions.
,
angular integration always results in proper inner analytic
functions, and therefore that this operation also stays within the space
of proper inner analytic functions.
Let us now prove that the operations of angular differentiation and of
angular integration are inverse operations to one another. Strictly
speaking, this is true within the subset of inner analytic functions that
have the additional property that ![]() , that is, for proper inner
analytic functions. Since any inner analytic function can be obtained from
a proper inner analytic function by the mere addition of a constant, this
is a very weak limitation. Let us consider then the space of proper inner
analytic functions.
, that is, for proper inner
analytic functions. Since any inner analytic function can be obtained from
a proper inner analytic function by the mere addition of a constant, this
is a very weak limitation. Let us consider then the space of proper inner
analytic functions.
We simply compose the two operations in the required order, and calculate in a straightforward manner, merely using the fundamental theorem of the calculus, to get
![$\displaystyle -\mbox{\boldmath$\imath$}
\int_{0}^{z}dz'\,
\frac{1}{z'}\,
\left[...
...'\,
\frac{dw}{dz'}(z')
-
\mbox{\boldmath$\imath$}
0\,
\frac{dw}{dz'}(0)
\right]$](img56.png) |
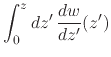 |
||
| (13) |
which is the original inner analytic function ![]() so long as
so long as ![]() ,
that is, for proper inner analytic functions, thus establishing this
property.
,
that is, for proper inner analytic functions, thus establishing this
property.
We simply compose the two operations in the required order, and calculate
in a straightforward manner, using this time the power-series
representation of the inner analytic function ![]() . First integrating
term by term and then differentiating term by term, both of which are
allowed operations for convergent power series, we get
. First integrating
term by term and then differentiating term by term, both of which are
allowed operations for convergent power series, we get
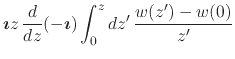 |
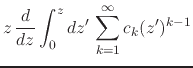 |
||
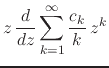 |
|||
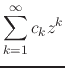 |
|||
| (14) |
which is the original inner analytic function ![]() so long as
so long as ![]() ,
that is, for proper inner analytic functions, thus establishing this
property.
,
that is, for proper inner analytic functions, thus establishing this
property.
With the use of the operations of angular differentiation and angular integration the space of proper inner analytic functions can now be organized as a collection of infinite discrete chains of functions, so that within each chain the functions are related to each other by either angular integrations or angular differentiations. This leads to the definition that follows.
Starting from an arbitrary proper inner analytic function ![]() , also
denoted as
, also
denoted as
![]() , one proceeds in the differentiation direction
to the functions
, one proceeds in the differentiation direction
to the functions
![]() ,
,
![]() ,
,
![]() , etc,
and in the integration direction to the functions
, etc,
and in the integration direction to the functions
![]() ,
,
![]() ,
,
![]() , etc. One thus produces an infinite
chain of proper inner analytic functions such as
, etc. One thus produces an infinite
chain of proper inner analytic functions such as
| (15) |
in which angular differentiation takes one to the right and angular integration takes one to the left. We name such a structure an integral-differential chain of proper inner analytic functions. We may refer to the proper inner analytic functions forming the chain as links in that chain.
Note that all the functions in such a chain have exactly the same set of singular points on the unit circle, although the character of these singularities will change from function to function along the chain. Note also that each such integral-differential chain induces, by means of the real parts of their inner analytic functions, a corresponding chain of real objects over the unit circle, when and where the limits from the open unit disk to the unit circle exist, or can be consistently defined. Finally note that, given a singularity at a certain point on the unit circle, the integral-differential chain also induces a corresponding chain of singularities at that point. Let us now prove an important property of these chains, namely that they do not intersect each other.
In order to prove this, we start by proving that, if two proper inner
analytic functions have the same angular derivative, then they must be
equal. If we have two such proper inner analytic functions ![]() and
and
![]() , the statement that they have the same angular derivative is
expressed as
, the statement that they have the same angular derivative is
expressed as
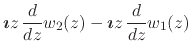 |
|||
![$\displaystyle \frac{d}{dz}[w_{2}(z)-w_{1}(z)]$](img73.png) |
|||
| (16) |
where ![]() is some complex constant, for all
is some complex constant, for all ![]() within the open unit disk,
including the case
within the open unit disk,
including the case ![]() , as one can see if one takes the limit
, as one can see if one takes the limit ![]() of the last equation above. However, since at
of the last equation above. However, since at ![]() we have that
we have that
![]() and
and ![]() , it then follows that
, it then follows that ![]() , so that we may
conclude that
, so that we may
conclude that
| (17) |
thus proving the point. A similar result is valid for two proper inner analytic functions that have the same angular primitive. Since we have already shown that angular integration and angular differentiation are inverse operations to each other, we can prove this by simply noting the trivial fact that the operation of angular differentiation cannot produce two different results for the same function. Therefore, there cannot exist two different proper inner analytic functions whose angular primitives are one and the same function.
We may now conclude that two different integral-differential chains of proper inner analytic functions can never have a member-function in common, because this would mean that two different proper inner analytic functions would have either the same angular derivative or the same angular primitive, neither of which is possible. It follows that each proper inner analytic function appears in one and only one of these integral-differential chains, which establishes this property.
Note, for future use, that there is a single integral-differential
chain of proper inner analytic functions which is a constant chain, in the
sense that all member-functions of the chain are equal, namely the null
chain, in which all members are the null function ![]() . It is
easy to verify that the differential equation
. It is
easy to verify that the differential equation
![]() has no
other inner analytic function as a solution. Note also that one may
consider all the non-proper inner analytic functions
has no
other inner analytic function as a solution. Note also that one may
consider all the non-proper inner analytic functions ![]() which are
related to a given proper inner analytic function
which are
related to a given proper inner analytic function ![]() to also
belong to the same link of the corresponding integral-differential
chain. Since all such functions have the form
to also
belong to the same link of the corresponding integral-differential
chain. Since all such functions have the form
| (18) |
where ![]() is a complex constant, this has the effect of associating to
each link of the integral-differential chain of
is a complex constant, this has the effect of associating to
each link of the integral-differential chain of ![]() a complex plane
of constants
a complex plane
of constants ![]() in which each point corresponds to a function
in which each point corresponds to a function ![]() . In
particular, all constant functions are associated to the null function,
and therefore to a complex plane of constants at each link of the null
chain.
. In
particular, all constant functions are associated to the null function,
and therefore to a complex plane of constants at each link of the null
chain.
We will now establish a general scheme for the classification of all possible singularities of inner analytic functions. This can be done for analytic functions in general, but we will do it here in a way that is particularly suited for our inner analytic functions.
Let ![]() be a point on the unit circle. A singularity of an inner
analytic function
be a point on the unit circle. A singularity of an inner
analytic function ![]() at
at ![]() is a soft singularity if the
limit of
is a soft singularity if the
limit of ![]() to that point exists and is finite. Otherwise, it is a
hard singularity.
to that point exists and is finite. Otherwise, it is a
hard singularity.
This is a complete classification of all possible singularities because, given a point of singularity, either the limit of the function to that point from within the open unit disk exists, or it does not. There is no third alternative, and therefore every singularity is either soft or hard. We may now establish the following important property of soft singularities.
In order to prove this first note that, since the singularity at ![]() is soft, the function
is soft, the function ![]() is defined by continuity there, being
therefore continuous at
is defined by continuity there, being
therefore continuous at ![]() . Consider now a curve contained within the
open unit disk, that connects to
. Consider now a curve contained within the
open unit disk, that connects to ![]() along some direction, that has a
finite length, and which is an otherwise arbitrary curve. We have at once
that
along some direction, that has a
finite length, and which is an otherwise arbitrary curve. We have at once
that ![]() is analytic at all points on this curve except
is analytic at all points on this curve except ![]() . It
follows that
. It
follows that ![]() is continuous, and thus that
is continuous, and thus that ![]() is continuous,
everywhere on this curve, including at
is continuous,
everywhere on this curve, including at ![]() . Hence, the limits of
. Hence, the limits of
![]() to all points on this curve exist and are finite positive real
numbers.
to all points on this curve exist and are finite positive real
numbers.
We now note that this set of finite real numbers must be bounded, because
otherwise there would be a hard singularity of ![]() somewhere within the
open unit disk, where this function is in fact analytic. We conclude
therefore that over the curve the function
somewhere within the
open unit disk, where this function is in fact analytic. We conclude
therefore that over the curve the function ![]() is a bounded continuous
function on a finite-length domain, which implies that
is a bounded continuous
function on a finite-length domain, which implies that ![]() is
integrable in that domain. Therefore, we may state that
is
integrable in that domain. Therefore, we may state that ![]() is
integrable along arbitrary curves reaching the point
is
integrable along arbitrary curves reaching the point ![]() from strictly
within the open unit disk2, which thus establishes this property.
from strictly
within the open unit disk2, which thus establishes this property.
We will now prove a couple of important further properties of the
singularity classification, one for soft singularities and one for hard
singularities. For this purpose, let ![]() be a point on the unit
circle. Let us discuss first a property of soft singularities, which is
related to angular integration.
be a point on the unit
circle. Let us discuss first a property of soft singularities, which is
related to angular integration.
In order to prove this we use the fact that a soft singularity is
necessarily an integrable one. We already know that if ![]() has a
singularity at
has a
singularity at ![]() , then so does its angular primitive
, then so does its angular primitive
![]() . If we now consider the angular primitive of
. If we now consider the angular primitive of ![]() at
at
![]() , we have
, we have
| (19) |
where the integral can be taken over any simple curve within the open unit
disk. We already know that the integrand is regular at the origin. Since
the singularity of ![]() at
at ![]() is soft, that singularity is
integrable along any simple curve within the open unit disk that goes from
is soft, that singularity is
integrable along any simple curve within the open unit disk that goes from
![]() to
to ![]() . Therefore, it follows that this integral exists and is
finite, and thus that
. Therefore, it follows that this integral exists and is
finite, and thus that
![]() exists and is finite. Since the
function
exists and is finite. Since the
function
![]() is thus well defined3 at
is thus well defined3 at ![]() ,
as well as analytic around that point, it follows that the singularity of
,
as well as analytic around that point, it follows that the singularity of
![]() at
at ![]() is also soft, which thus establishes this
property.
is also soft, which thus establishes this
property.
Let us discuss now a property of hard singularities, which is related to angular differentiation.
If ![]() has a hard singularity at
has a hard singularity at ![]() , then it is not well defined
there, implying that it is not continuous there, and therefore that it is
also not differentiable there. This clearly implies that the angular
derivative
, then it is not well defined
there, implying that it is not continuous there, and therefore that it is
also not differentiable there. This clearly implies that the angular
derivative
![]() of
of ![]() , which we already know to also have a
singularity at
, which we already know to also have a
singularity at ![]() , is not well defined there as well. This in turn
implies that the singularity of
, is not well defined there as well. This in turn
implies that the singularity of
![]() at
at ![]() must be a hard
one.
must be a hard
one.
However, the simplest way to prove this property is to note that it
follows from the previous one, that is, from Property 5.2.
We can prove it by reductio ad absurdum, using the fact that, as we have
already shown, the operations of angular differentiation and angular
integration are inverse operations to each other. If we assume that ![]() has a hard singularity at
has a hard singularity at ![]() and that
and that
![]() has a soft
singularity at that point, then we have an inner analytic function, namely
has a soft
singularity at that point, then we have an inner analytic function, namely
![]() , that has a soft singularity at
, that has a soft singularity at ![]() , while its angular
primitive, namely
, while its angular
primitive, namely ![]() , has a hard singularity at that point. However,
according to Property 5.2 this is impossible, since angular
integration always takes a soft singularity to another soft singularity.
This establishes, therefore, that this property holds.
, has a hard singularity at that point. However,
according to Property 5.2 this is impossible, since angular
integration always takes a soft singularity to another soft singularity.
This establishes, therefore, that this property holds.
The use of the operations of angular differentiation and of angular
integration now leads to a refinement of our general classification of
singularities. We will use them to assign to each singularity a degree of softness or a degree of hardness. Let ![]() be an
inner analytic function and
be an
inner analytic function and ![]() a point on the unit circle, and
consider the following two definitions.
a point on the unit circle, and
consider the following two definitions.
Let us assume that ![]() has a soft singularity at
has a soft singularity at ![]() . If an
arbitrarily large number of successive angular differentiations of
. If an
arbitrarily large number of successive angular differentiations of ![]() always results in a singularity at
always results in a singularity at ![]() which is still soft, then we
say that the singularity of
which is still soft, then we
say that the singularity of ![]() at
at ![]() is an infinitely soft
singularity. Otherwise, if
is an infinitely soft
singularity. Otherwise, if ![]() is the minimum number of angular
differentiations that have to be applied to
is the minimum number of angular
differentiations that have to be applied to ![]() in order for the
singularity at
in order for the
singularity at ![]() to become a hard one, then we define
to become a hard one, then we define ![]() as the
degree of softness of the original singularity of
as the
degree of softness of the original singularity of ![]() at
at
![]() . Therefore, a degree of softness is an integer
. Therefore, a degree of softness is an integer
![]() .
.
Let us assume that ![]() has a hard singularity at
has a hard singularity at ![]() . If an
arbitrarily large number of successive angular integrations of
. If an
arbitrarily large number of successive angular integrations of ![]() always results in a singularity at
always results in a singularity at ![]() which is still hard, then we
say that the singularity of
which is still hard, then we
say that the singularity of ![]() at
at ![]() is an infinitely hard
singularity. Otherwise, if
is an infinitely hard
singularity. Otherwise, if ![]() is the minimum number of angular
integrations that have to be applied to
is the minimum number of angular
integrations that have to be applied to ![]() in order for the
singularity at
in order for the
singularity at ![]() to become a soft one, then we define
to become a soft one, then we define ![]() as the
degree of hardness of the original singularity of
as the
degree of hardness of the original singularity of ![]() at
at ![]() .
Therefore, a degree of hardness is an integer
.
Therefore, a degree of hardness is an integer
![]() .
.
In order to see that this establishes a complete classification of all possible singularities, let us examine all the possible outcomes when we apply angular differentiations and angular integrations to inner analytic functions. We already saw that, if we apply a angular integration to a soft singularity, then the result is always another soft singularity. Similarly we saw that, if we apply a angular differentiation to a hard singularity, then the result is always another hard singularity. The two remaining alternatives are the application of a angular integration to a hard singularity, and the application of a angular differentiation to a soft singularity. In these two cases the resulting singularity may be either soft or hard, and the remaining possibilities were dealt with in Definitions 6 and 7. Since this applies to all singularities in all integral-differential chains, it applies to all possible singularities of all inner analytic functions.
In some cases examples of this classification are well known. For
instance, a simple example of an infinitely hard singularity is any
essential singularity. Examples of infinitely soft singularities are
harder to come by, and they are related to integrable real functions which
are infinitely differentiable but not analytic. A simple example of a hard
singularity with degree of hardness ![]() is a pole of order
is a pole of order ![]() .
Examples of soft singularities are the square root, and products of
strictly positive powers with the logarithm.
.
Examples of soft singularities are the square root, and products of
strictly positive powers with the logarithm.
If a singularity at a given singular point ![]() on the unit circle is
either infinitely soft or infinitely hard, then the corresponding
integral-differential chain of singularities contains either only soft
singularities or only hard singularities. If the singularity is neither
infinitely soft nor infinitely hard, then at some point along the
corresponding integral-differential chain the character of the singularity
changes, and from that point on the soft or hard character remains
constant at the new value throughout the rest of the integral-differential
chain in that direction. Therefore, in each integral-differential chain
that does not consist of either only soft singularities or only hard
singularities, there is a single transition between two functions on the
chain where the character of the singularity changes.
on the unit circle is
either infinitely soft or infinitely hard, then the corresponding
integral-differential chain of singularities contains either only soft
singularities or only hard singularities. If the singularity is neither
infinitely soft nor infinitely hard, then at some point along the
corresponding integral-differential chain the character of the singularity
changes, and from that point on the soft or hard character remains
constant at the new value throughout the rest of the integral-differential
chain in that direction. Therefore, in each integral-differential chain
that does not consist of either only soft singularities or only hard
singularities, there is a single transition between two functions on the
chain where the character of the singularity changes.
Let us examine in more detail the important intermediary case in which we assign to the singularity the degree of hardness zero, which we will also describe as that of a borderline hard singularity.
Given an inner analytic function ![]() and a point
and a point ![]() on the unit
circle where it has a hard singularity, if a single angular
integration of
on the unit
circle where it has a hard singularity, if a single angular
integration of ![]() results in a function
results in a function
![]() which has at
which has at
![]() a soft singularity, then we say that the original function
a soft singularity, then we say that the original function ![]() has at
has at ![]() a borderline hard singularity, that is, a hard
singularity with degree of hardness zero.
a borderline hard singularity, that is, a hard
singularity with degree of hardness zero.
We establish now the following important property of borderline hard singularities.
This is so because the angular integration of ![]() produces an inner
analytic function
produces an inner
analytic function
![]() which has at
which has at ![]() a soft
singularity, and therefore is well defined at that point. Since the value
of
a soft
singularity, and therefore is well defined at that point. Since the value
of
![]() at
at ![]() is given by an integral of
is given by an integral of ![]() along a
curve reaching that point, that integral must therefore exist and result
in a finite complex number4. Therefore, the singularity of
along a
curve reaching that point, that integral must therefore exist and result
in a finite complex number4. Therefore, the singularity of ![]() at
at ![]() must be an integrable one. We may thus conclude that all borderline hard
singularities are integrable ones, which establishes this property.
must be an integrable one. We may thus conclude that all borderline hard
singularities are integrable ones, which establishes this property.
The transition between a borderline hard singularity and a soft
singularity is therefore the single point of transition of the soft or
hard character of the singularities along the corresponding
integral-differential chain. Starting from a borderline hard singularity,
![]() angular integrations produce a soft singularity with degree of
softness
angular integrations produce a soft singularity with degree of
softness ![]() , and
, and ![]() angular differentiations produce a hard
singularity with degree or hardness
angular differentiations produce a hard
singularity with degree or hardness ![]() . Note that a strictly positive
degree of softness given by
. Note that a strictly positive
degree of softness given by ![]() can be identified with a negative degree
of hardness given by
can be identified with a negative degree
of hardness given by ![]() , and vice-versa. A simple example of a
borderline hard singularity is a logarithmic singularity.
, and vice-versa. A simple example of a
borderline hard singularity is a logarithmic singularity.
Let us end this section with one more important property of hard singularities.
If a hard singularity of ![]() at
at ![]() has a degree of hardness of one
or larger, then by angular integration it is mapped to another hard
singularity, the hard singularity of
has a degree of hardness of one
or larger, then by angular integration it is mapped to another hard
singularity, the hard singularity of
![]() at
at ![]() . If the
hard singularity of
. If the
hard singularity of ![]() were integrable, then
were integrable, then
![]() would be
well defined at
would be
well defined at ![]() , and therefore its singularity would be soft
rather than hard. Since we know that the singularity of
, and therefore its singularity would be soft
rather than hard. Since we know that the singularity of
![]() is hard, it follows that the singularity of
is hard, it follows that the singularity of ![]() cannot be integrable.
In other words, all hard singularities with strictly positive degrees of
hardness are necessarily non-integrable singularities, which establishes
this property.
cannot be integrable.
In other words, all hard singularities with strictly positive degrees of
hardness are necessarily non-integrable singularities, which establishes
this property.
Note that the structure of the integral-differential chains establishes within the space of proper inner analytic functions what may be described as a structure of discrete fibers, in which the whole space is decomposed as a set of non-intersecting discrete linear structures. The same is then true for the corresponding real objects on the unit circle. One can then reconstruct the space of all inner analytic functions by associating to each link of each integral-differential chain a complex plane of constants to be added to the proper inner analytic function of that link, in order to get all the non-proper inner analytic functions associated to it. In terms of the corresponding real functions, this corresponds to the association to each link of a real line of real constants.