Next: Behavior Under Analytic Operations Up: Complex Analysis of Real Previous: Definitions and Properties
In this section we will establish the relation between integrable real functions and inner analytic functions. When we discuss real functions in this paper, some properties will be globally assumed for these functions. These are rather weak conditions to be imposed on these functions, that will be in force throughout this paper. It is to be understood, without any need for further comment, that these conditions are valid whenever real functions appear in the arguments. These weak conditions certainly hold for any integrable real functions that are obtained as restrictions of corresponding inner analytic functions to the unit circle. The most basic condition is that the real functions must be measurable in the sense of Lebesgue, with the usual Lebesgue measure [#!RARudin!#,#!RARoyden!#]. In essence, this is basic infrastructure to allow the functions to be integrable.
In order to discuss the other global conditions, we must first discuss the classification of singularities of a real function. The concept of a singularity itself is the same as that for a complex function, namely a point where the function is not analytic. The concept of a removable singularity is well-known for analytic functions in the complex plane. What we mean by a removable singularity in the case of real functions on the unit circle is a singular point such that both lateral limits of the function to that point exist and result in the same real value, but where the function has been arbitrarily defined to have some other real value. This is therefore a point were the function can be redefined by continuity, resulting in a continuous function at that point. The concepts of soft and hard singularities are carried in a straightforward way from the case of complex functions, discussed in Section 2, to that of real functions. The only difference is that the concept of the limit of the function to the point is now taken to be the real one, along the unit circle.
The second global condition we will impose is that the functions have no removable singularities. Since they can be easily eliminated, these are trivial singularities, which we will simply rule out of our discussions in this paper. Although the presence of even a denumerably infinite set of such trivial singularities does not significantly affect the results to be presented here, their elimination does significantly simplify the arguments to be presented. It is for this reason, that is, for the sake of simplicity, that we rule out such irrelevant singularities. In addition to this we will require, as our third an last global condition, that the number of hard singularities be finite, and hence that they be all isolated from one another. There will be no limitation on the number of soft singularities. In terms of the more immediate characteristics of the real functions, the relevant requirement is that the number of singular points where a given real function diverges to infinity be finite.
In this section we will prove the following theorem.
Given an arbitrary real function defined within an arbitrary finite closed
interval, it can always be mapped to a real function within the periodic
interval ![]() , by a simple linear change of variables, so it
suffices for our purposes here to examine only the set of real functions
, by a simple linear change of variables, so it
suffices for our purposes here to examine only the set of real functions
![]() defined in this standard interval. The interval is then mapped
onto the unit circle of the complex
defined in this standard interval. The interval is then mapped
onto the unit circle of the complex ![]() plane. What happens to the values
of the function at the two ends of the interval when one does this is
irrelevant for our purposes here, but for definiteness we may think that
one attributes to the function at the point
plane. What happens to the values
of the function at the two ends of the interval when one does this is
irrelevant for our purposes here, but for definiteness we may think that
one attributes to the function at the point ![]() the arithmetic average
of the values of the function at the two ends of the periodic interval.
The further requirements to be imposed on these functions are still quite
weak, namely no more than that they be Lebesgue-integrable in the periodic
interval, so that one can attribute to them a set of Fourier
coefficients [#!FSchurchill!#].
the arithmetic average
of the values of the function at the two ends of the periodic interval.
The further requirements to be imposed on these functions are still quite
weak, namely no more than that they be Lebesgue-integrable in the periodic
interval, so that one can attribute to them a set of Fourier
coefficients [#!FSchurchill!#].
Since for Lebesgue-measurable functions defined within a compact interval plain integrability and absolute integrability are equivalent requirements [#!RARudin!#,#!RARoyden!#], we may assume that the functions are absolutely integrable, without loss of generality. Note that the functions do not have to be differentiable or even continuous. They may also be unlimited, possibly diverging to infinity at some singular points, so long as they are absolutely integrable. This means, of course, that any hard singularities that they may have at isolated points must be integrable singularities, which we may thus characterize as borderline hard singularities, in a real sense of the term. This means, in turn, that although the functions may diverge to infinity at isolated points, their pairs of asymptotic integrals around these points must still exist and be finite real numbers.
This in turn means that these borderline hard singularities must be
surrounded by open intervals where there are no other borderline hard
singularities, so that the asymptotic integrals around the singular points
can be well defined and finite. It follows that any existing borderline
hard singularities must be isolated from any other borderline hard
singularities. Note that they do not really have to be isolated
singularities in the usual, strict sense of complex analysis, which would
require that they be isolated from all other singularities. All that
is required is that the borderline hard singularities be isolated from
each other. Hence the requirement that the number of hard singularities be
finite. Note also that one can have any number of soft singularities, even
an infinite number of them. As we pointed out before, in terms of the
properties of the real functions ![]() , the important requirement is
that the number of singular points on the unit circle where a given real
function diverges to infinity be finite.
, the important requirement is
that the number of singular points on the unit circle where a given real
function diverges to infinity be finite.
With all these preliminaries stated, the first thing that we must do here
is, given an arbitrary integrable real function ![]() defined within
the periodic interval
defined within
the periodic interval ![]() , to build from it an analytic function
, to build from it an analytic function
![]() within the open unit disk of the complex plane. For this purpose we
will use the Fourier coefficients of the given real function. The Fourier
coefficients [#!FSchurchill!#] are defined by
within the open unit disk of the complex plane. For this purpose we
will use the Fourier coefficients of the given real function. The Fourier
coefficients [#!FSchurchill!#] are defined by
where the set of functions
![]() , constitutes the Fourier basis of
functions. Since
, constitutes the Fourier basis of
functions. Since ![]() is absolutely integrable, we have that
is absolutely integrable, we have that
| (21) |
where ![]() is a positive and finite real number, namely the average value,
on the periodic interval
is a positive and finite real number, namely the average value,
on the periodic interval ![]() , of the absolute value of the
function. If we use the triangle inequalities, it follows therefore that
, of the absolute value of the
function. If we use the triangle inequalities, it follows therefore that
![]() exists and that it satisfies
exists and that it satisfies
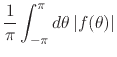 |
|||
| (22) |
that is, it is limited by ![]() . Since the elements of the Fourier basis
are all limited smooth functions, and using again the triangle
inequalities, it now follows that all other Fourier coefficients also
exist, and are also all limited by
. Since the elements of the Fourier basis
are all limited smooth functions, and using again the triangle
inequalities, it now follows that all other Fourier coefficients also
exist, and are also all limited by ![]() ,
,
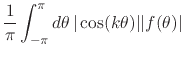 |
|||
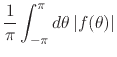 |
|||
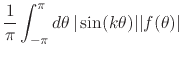 |
|||
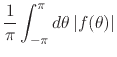 |
|||
| (23) |
for all ![]() , since the absolute values of the sines and cosines are
limited by one. Given that we have the coefficients
, since the absolute values of the sines and cosines are
limited by one. Given that we have the coefficients ![]() and
and
![]() , the construction of the corresponding inner analytic function
is now straightforward. We simply define the set of complex coefficients
, the construction of the corresponding inner analytic function
is now straightforward. We simply define the set of complex coefficients
for
![]() . Note that these coefficients are all
limited by
. Note that these coefficients are all
limited by ![]() , since, using once more the triangle inequalities, we have
, since, using once more the triangle inequalities, we have
| (25) |
We now define a complex variable ![]() associated to
associated to ![]() , using an
auxiliary positive real variable
, using an
auxiliary positive real variable ![]() ,
,
| (26) |
where ![]() are polar coordinates in the complex
are polar coordinates in the complex ![]() plane. We
then construct the following power series around the origin
plane. We
then construct the following power series around the origin ![]() ,
,
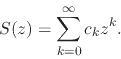 |
(27) |
According to the theorems of complex analysis [#!CVchurchill!#], where
this power series converges in the complex ![]() plane, it converges
absolutely and uniformly to an analytic function
plane, it converges
absolutely and uniformly to an analytic function ![]() . It then follows
that
. It then follows
that ![]() is in fact the Taylor series of
is in fact the Taylor series of ![]() around
around ![]() . We must
now establish that this series converges within the open unit disk,
whatever the values of the Fourier coefficients, given only that they are
all limited by
. We must
now establish that this series converges within the open unit disk,
whatever the values of the Fourier coefficients, given only that they are
all limited by ![]() . In order to do this we will first prove that the
series
. In order to do this we will first prove that the
series ![]() is absolutely convergent, that is, we will establish the
convergence of the corresponding series of absolute values
is absolutely convergent, that is, we will establish the
convergence of the corresponding series of absolute values
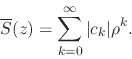 |
(28) |
Let us now consider the partial sums of this real series, and replace the absolute values of the coefficients by their common upper bound,
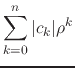 |
|||
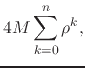 |
(29) |
where
![]() . This is now the sum of a geometric
progression, so that we have
. This is now the sum of a geometric
progression, so that we have
| (30) |
For ![]() we may now take the
we may now take the ![]() limit of the right-hand
side, without violating the inequality, so that we get the sum of a
geometric series,
limit of the right-hand
side, without violating the inequality, so that we get the sum of a
geometric series,
| (31) |
For ![]() the right-hand side is now a positive upper bound for all the
partial sums of the series of absolute values. Therefore, since the
sequence
the right-hand side is now a positive upper bound for all the
partial sums of the series of absolute values. Therefore, since the
sequence
![]() of partial sums is a monotonically
increasing sequence of real numbers which is bounded from above, it now
follows that this real sequence is necessarily a convergent one.
of partial sums is a monotonically
increasing sequence of real numbers which is bounded from above, it now
follows that this real sequence is necessarily a convergent one.
Therefore the series of absolute values
![]() is convergent on
the open unit disk
is convergent on
the open unit disk ![]() , which in turn implies that the original
series
, which in turn implies that the original
series ![]() is absolutely convergent on that same disk. This then
implies that the series
is absolutely convergent on that same disk. This then
implies that the series ![]() is simply convergent on that same disk.
Since
is simply convergent on that same disk.
Since ![]() is a convergent power series, it converges to an analytic
function on the open unit disk, which we may now name
is a convergent power series, it converges to an analytic
function on the open unit disk, which we may now name ![]() . Since this
is an analytic function within the open unit disk, it is an inner analytic
function, the one that corresponds to the real function
. Since this
is an analytic function within the open unit disk, it is an inner analytic
function, the one that corresponds to the real function ![]() on the
unit circle,
on the
unit circle,
| (32) |
The coefficients ![]() are now recognized as the Taylor coefficients of
the inner analytic function
are now recognized as the Taylor coefficients of
the inner analytic function ![]() with respect to the origin. We have
therefore established that from any integrable real function
with respect to the origin. We have
therefore established that from any integrable real function ![]() one can define a unique corresponding inner analytic function
one can define a unique corresponding inner analytic function ![]() . This
completes the first part of the proof of Theorem 1.
. This
completes the first part of the proof of Theorem 1.
Next we must establish that ![]() can be recovered as the limit
can be recovered as the limit
![]() , from the open unit disk to the unit circle, of the real
part of
, from the open unit disk to the unit circle, of the real
part of ![]() , so that we can establish the complete correspondence
between the integrable real function and the inner analytic function,
, so that we can establish the complete correspondence
between the integrable real function and the inner analytic function,
| (33) |
We start by writing the coefficients ![]() in terms of
in terms of ![]() and
discussing their dependence on
and
discussing their dependence on ![]() . Since the complex coefficients
. Since the complex coefficients
![]() are the coefficients of the Taylor series of
are the coefficients of the Taylor series of ![]() around
around ![]() ,
the Cauchy integral formulas of complex analysis, for the function
,
the Cauchy integral formulas of complex analysis, for the function ![]() and its derivatives, written at
and its derivatives, written at ![]() for the
for the ![]() derivative of
derivative of
![]() , tell us that we have
, tell us that we have
for all ![]() , where
, where ![]() is any simple closed curve within the open unit
disk that contains the origin, which we may now take as a circle centered
at
is any simple closed curve within the open unit
disk that contains the origin, which we may now take as a circle centered
at ![]() with radius
with radius ![]() . We now note that, since
. We now note that, since ![]() is
analytic in the open unit disk, so that the explicit singularity at
is
analytic in the open unit disk, so that the explicit singularity at ![]() is the only singularity of the integrand on that disk, by the
Cauchy-Goursat theorem the integral is independent of
is the only singularity of the integrand on that disk, by the
Cauchy-Goursat theorem the integral is independent of ![]() within the
open unit disk, and therefore so are the complex coefficients
within the
open unit disk, and therefore so are the complex coefficients ![]() .
.
It thus follows that the coefficients ![]() are continuous functions of
are continuous functions of
![]() inside the open unit disk, and therefore that their
inside the open unit disk, and therefore that their
![]() limits exist and have those same constant values. Since we have
the relations in Equation (24), the same is true for the
Fourier coefficients
limits exist and have those same constant values. Since we have
the relations in Equation (24), the same is true for the
Fourier coefficients ![]() and
and ![]() . On the other hand, by
construction these are the same coefficients that were obtained from the
real function
. On the other hand, by
construction these are the same coefficients that were obtained from the
real function ![]() on the unit circle, and we may thus conclude
that the coefficients
on the unit circle, and we may thus conclude
that the coefficients ![]() ,
, ![]() and
and ![]() , for all
, for all ![]() ,
are all constant with
,
are all constant with ![]() and therefore continuous functions of
and therefore continuous functions of ![]() in the whole closed unit disk. This means that, at least in the case
of the coefficients, the
in the whole closed unit disk. This means that, at least in the case
of the coefficients, the
![]() limit can be taken trivially.
limit can be taken trivially.
Let us now establish the fact that ![]() and the real part
and the real part
![]() of
of ![]() at
at ![]() have exactly the same set of Fourier
coefficients. We consider first the case of the coefficient
have exactly the same set of Fourier
coefficients. We consider first the case of the coefficient ![]() .
If we write the Cauchy integral formula in Equation (34) for
the case
.
If we write the Cauchy integral formula in Equation (34) for
the case ![]() we get
we get
| (35) |
Recalling that
![]() and writing the integral on the circle
of radius
and writing the integral on the circle
of radius ![]() using the integration variable
using the integration variable ![]() we get
we get
| (36) |
Since ![]() is real, we conclude that the imaginary part in the
right-hand side must be zero, and thus obtain
is real, we conclude that the imaginary part in the
right-hand side must be zero, and thus obtain
| (37) |
thus proving that ![]() , which is the
, which is the ![]() Fourier coefficient of
Fourier coefficient of
![]() , is also the
, is also the ![]() Fourier coefficient of
Fourier coefficient of
![]() ,
for any value of
,
for any value of ![]() , and thus is, in particular, the
, and thus is, in particular, the ![]() Fourier
coefficient of
Fourier
coefficient of ![]() . This is so because, since the
. This is so because, since the
![]() limit of the coefficient
limit of the coefficient ![]() can be taken, so can the
limit of the integral in the right-hand side. Note that this shows, in
particular, that
can be taken, so can the
limit of the integral in the right-hand side. Note that this shows, in
particular, that ![]() is an integrable real function. In order to
extend the analysis of the coefficients to the case
is an integrable real function. In order to
extend the analysis of the coefficients to the case ![]() we must first
derive some preliminary relations. Consider therefore the following
integral, on the same circuit
we must first
derive some preliminary relations. Consider therefore the following
integral, on the same circuit ![]() we used in Equation (34),
we used in Equation (34),
| (38) |
with ![]() . The integral is zero by the Cauchy-Goursat theorem, since for
. The integral is zero by the Cauchy-Goursat theorem, since for
![]() the integrand is analytic on the whole open unit disk. As before
we write the integral on the circle of radius
the integrand is analytic on the whole open unit disk. As before
we write the integral on the circle of radius ![]() using the integration
variable
using the integration
variable ![]() , to get
, to get
![$\displaystyle \int_{-\pi}^{\pi}d\theta\,
\left[
u(\rho,\theta)\cos(k\theta)
-
v(\rho,\theta)\sin(k\theta)
\right]
\hspace{1em}$](img166.png) |
|||
![$\displaystyle +
\mbox{\boldmath$\imath$}
\int_{-\pi}^{\pi}d\theta\,
\left[
u(\rho,\theta)\sin(k\theta)
+
v(\rho,\theta)\cos(k\theta)
\right]$](img167.png) |
(39) |
We are therefore left with the two identities involving
![]() and
and
![]() ,
,
which are valid for all ![]() and for all
and for all ![]() . If we now write
the integrals of the Cauchy integral formulas in Equation (34)
explicitly as integrals on
. If we now write
the integrals of the Cauchy integral formulas in Equation (34)
explicitly as integrals on ![]() , we get
, we get
![$\displaystyle \frac{\rho^{-k}}{2\pi}
\left\{
\int_{-\pi}^{\pi}d\theta\,
\left[
u(\rho,\theta)\cos(k\theta)
+
v(\rho,\theta)\sin(k\theta)
\right]
\right.$](img173.png) |
|||
![$\displaystyle \hspace{2.4em}
\left.
+
\mbox{\boldmath$\imath$}
\int_{-\pi}^{\pi...
...[
-
u(\rho,\theta)\sin(k\theta)
+
v(\rho,\theta)\cos(k\theta)
\right]
\right\}.$](img174.png) |
(41) |
Using the identities in Equation (40) in order to eliminate
![]() in favor of
in favor of
![]() and recalling that
and recalling that
![]() we get
we get
![\begin{displaymath}
\alpha_{k}
-
\mbox{\boldmath$\imath$}
\beta_{k}
=
\fra...
...mbox{\boldmath$\imath$}
u(\rho,\theta)\sin(k\theta)
\right],
\end{displaymath}](img176.png) |
(42) |
so that we have the relations for the Fourier coefficients,
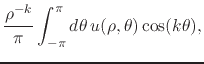 |
|||
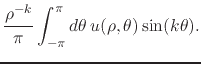 |
(43) |
Since the
![]() limits of the coefficients in the left-hand
sides can be taken, so can the
limits of the coefficients in the left-hand
sides can be taken, so can the
![]() limits of the integrals
in the right-hand sides. Therefore, taking the limit we have for the
Fourier coefficients,
limits of the integrals
in the right-hand sides. Therefore, taking the limit we have for the
Fourier coefficients,
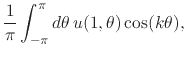 |
|||
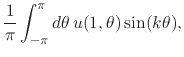 |
(44) |
thus completing the proof that the real functions ![]() and
and
![]() have exactly the same set of Fourier coefficients. Note, in
passing, that due to the identities in Equation (40) these
same coefficients can also be written in terms of
have exactly the same set of Fourier coefficients. Note, in
passing, that due to the identities in Equation (40) these
same coefficients can also be written in terms of ![]() ,
,
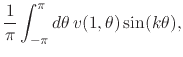 |
|||
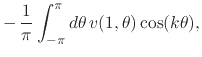 |
(45) |
in which the ![]() was exchanged for
was exchanged for ![]() and the
and the
![]() was exchanged for
was exchanged for
![]() . In fact, this is one
way to state that
. In fact, this is one
way to state that ![]() and
and ![]() are two mutually
Fourier-conjugate real functions.
are two mutually
Fourier-conjugate real functions.
Let us now examine the limit
![]() that allows us to recover
from the real part
that allows us to recover
from the real part
![]() of the inner analytic function
of the inner analytic function ![]() the original real function
the original real function ![]() . We want to establish that we may
state that
. We want to establish that we may
state that
| (46) |
almost everywhere. Let us prove that ![]() and
and ![]() must
coincide almost everywhere. Simply consider the real function
must
coincide almost everywhere. Simply consider the real function ![]() given by
given by
| (47) |
where
| (48) |
Since it is the difference of two integrable real functions, ![]() is itself an integrable real function. However, since the expression of
the Fourier coefficients is linear on the functions, and since
is itself an integrable real function. However, since the expression of
the Fourier coefficients is linear on the functions, and since
![]() and
and ![]() have exactly the same set of Fourier
coefficients, it is clear that all the Fourier coefficients of
have exactly the same set of Fourier
coefficients, it is clear that all the Fourier coefficients of ![]() are zero. Therefore, for the integrable real function
are zero. Therefore, for the integrable real function ![]() we have
that
we have
that ![]() for all
for all ![]() , and thus the inner analytic function that
corresponds to
, and thus the inner analytic function that
corresponds to ![]() is the identically null complex function
is the identically null complex function
![]() . This is an inner analytic function which is, in
fact, analytic over the whole complex plane, and which, in particular, is
zero over the unit circle, so that we have5
. This is an inner analytic function which is, in
fact, analytic over the whole complex plane, and which, in particular, is
zero over the unit circle, so that we have5
![]() . Note, in particular, that the
. Note, in particular, that the
![]() limits exist at all points of the unit circle in the case of the
inner analytic function associated to
limits exist at all points of the unit circle in the case of the
inner analytic function associated to ![]() . Since our argument is
based on the Fourier coefficients
. Since our argument is
based on the Fourier coefficients ![]() and
and ![]() , which in
turn are given by integrals involving these functions, we can conclude
only that
, which in
turn are given by integrals involving these functions, we can conclude
only that
| (49) |
is valid almost everywhere over the unit circle. Therefore, we have
concluded that the
![]() limit of
limit of ![]() exists and that the
limit of its real part
exists and that the
limit of its real part
![]() results in the values of
results in the values of
![]() almost everywhere. This concludes the proof of
Theorem 1.
almost everywhere. This concludes the proof of
Theorem 1.
Regarding the fact that the proof above is valid only almost everywhere,
it is possible to characterize, up to a certain point, the set of points
where the recovery of the real function ![]() may fail, using the
character of the possible singularities of the corresponding inner
analytic function
may fail, using the
character of the possible singularities of the corresponding inner
analytic function ![]() . Wherever
. Wherever ![]() is either analytic or has only
soft singularities on the unit circle, the
is either analytic or has only
soft singularities on the unit circle, the
![]() limit exists,
and therefore the values of
limit exists,
and therefore the values of ![]() can be recovered. At points on the
unit circle where
can be recovered. At points on the
unit circle where ![]() has hard singularities,
has hard singularities, ![]() necessarily
also has hard singularities, and therefore the limit does not exist and
thus the values of
necessarily
also has hard singularities, and therefore the limit does not exist and
thus the values of ![]() cannot be recovered. However, in this case
this fact is irrelevant, since
cannot be recovered. However, in this case
this fact is irrelevant, since ![]() is not well defined at these
points to begin with. In any case, by hypothesis there can be at most a
finite number of such points, which therefore form a zero-measure set.
is not well defined at these
points to begin with. In any case, by hypothesis there can be at most a
finite number of such points, which therefore form a zero-measure set.
Therefore, the only points where ![]() may exist but not be
recoverable from the real part of
may exist but not be
recoverable from the real part of ![]() are those singular points on the
unit circle where
are those singular points on the
unit circle where ![]() has a soft singularity, in the real
sense of the term, while
has a soft singularity, in the real
sense of the term, while ![]() has a hard singularity, in the
complex sense of the term. In principle this is possible because the
requirement for a singularity to be soft in the complex case is more
restrictive than the corresponding requirement in the real case. For a
singularity to be soft in the real case it suffices that the limits of the
function to the point exist and be the same only along two directions,
coming from either side along the unit circle, but for the singularity to
be soft in the complex case the limits must exist and be the same along
all directions.
has a hard singularity, in the
complex sense of the term. In principle this is possible because the
requirement for a singularity to be soft in the complex case is more
restrictive than the corresponding requirement in the real case. For a
singularity to be soft in the real case it suffices that the limits of the
function to the point exist and be the same only along two directions,
coming from either side along the unit circle, but for the singularity to
be soft in the complex case the limits must exist and be the same along
all directions.
It is indeed possible for a hard complex singularity on the unit circle to be so oriented that the limit exists along the two particular directions along the unit circle, but does not exist along other directions. For example, consider the rather pathological real function
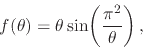 |
(50) |
for
![]() and
and
![]() . It is well known that this
function has an essential singularity at
. It is well known that this
function has an essential singularity at ![]() in the complex
in the complex
![]() plane, which is an infinitely hard singularity. However, if
defined by continuity at
plane, which is an infinitely hard singularity. However, if
defined by continuity at ![]() the function is continuous there, and
therefore the singularity at
the function is continuous there, and
therefore the singularity at ![]() is a soft one in the real sense of
the term. The function is also continuous at all other points on the unit
circle. We now observe that, despite having an infinitely hard complex
singularity at
is a soft one in the real sense of
the term. The function is also continuous at all other points on the unit
circle. We now observe that, despite having an infinitely hard complex
singularity at ![]() , this is a limited real function on a finite
domain and therefore an integrable real function, which means that we may
still construct an inner analytic function that corresponds to it.
Presumably, this inner analytic function also has an essential singularity
at the point
, this is a limited real function on a finite
domain and therefore an integrable real function, which means that we may
still construct an inner analytic function that corresponds to it.
Presumably, this inner analytic function also has an essential singularity
at the point ![]() , which corresponds to
, which corresponds to ![]() on the unit circle.
This fact would then prevent us from obtaining the value of the function
at
on the unit circle.
This fact would then prevent us from obtaining the value of the function
at ![]() as the
as the
![]() limit of the real part of that
inner analytic function.
limit of the real part of that
inner analytic function.
The mere fact that one can establish that there is a well defined inner analytic function for such a pathological real function is in itself rather unexpected and surprising. Furthermore, one can easily see that this is not the only example. One can also consider the related example, this time one in which the singularity is not soft in the real sense of the term,
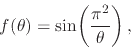 |
(51) |
which is still a limited real function on a finite domain and therefore an integrable real function, which again means that we may still construct an inner analytic function that corresponds to it. Many other variations of these examples can be constructed without too much difficulty.
Excluding all such exceptional cases, we may consider that the recovery of
the real function ![]() as the
as the
![]() limit of the real
part of the inner analytic function holds everywhere in the domain of
definition of
limit of the real
part of the inner analytic function holds everywhere in the domain of
definition of ![]() , that is, wherever it is well defined. In order
to exclude all such exceptional cases, all we have to do is to exchange
the condition that there be at most a finite number of hard singularities,
in the real sense of the term, of the integrable real function
, that is, wherever it is well defined. In order
to exclude all such exceptional cases, all we have to do is to exchange
the condition that there be at most a finite number of hard singularities,
in the real sense of the term, of the integrable real function
![]() , for the condition that there be at most a finite number of
hard singularities with finite degrees of hardness, in the complex sense
of the term, of the corresponding inner analytic
function6
, for the condition that there be at most a finite number of
hard singularities with finite degrees of hardness, in the complex sense
of the term, of the corresponding inner analytic
function6 ![]() .
.
Once we have the inner analytic function that corresponds to a given
integrable real function, we may consider the integral-differential chain
to which it belongs. There are two particular cases that deserve mention
here. One is that in which the inner analytic functions in the chain do
not have any singularities at all on the unit circle, in which case the
corresponding real functions are all analytic functions of ![]() in the
real sense of the term. The other is that in which the inner analytic
functions in the chain have only infinitely soft singularities on the unit
circle, in which case the corresponding real functions are all infinitely
differentiable functions of
in the
real sense of the term. The other is that in which the inner analytic
functions in the chain have only infinitely soft singularities on the unit
circle, in which case the corresponding real functions are all infinitely
differentiable functions of ![]() , although they are not analytic. In
this case one can go indefinitely along the chain in either direction
without any change in the soft character of the singularities.
, although they are not analytic. In
this case one can go indefinitely along the chain in either direction
without any change in the soft character of the singularities.
If, on the other hand, one does have borderline hard singularities or soft singularities with finite degrees of softness, then at some point along the chain there will be a transition to one or more hard singularities with strictly positive degrees of hardness, which do not necessarily correspond to integrable real functions. It can be shown that most of these singularities are instead associated to either singular distributions or non-integrable real functions. Their discussion will be postponed to the aforementioned forthcoming papers.