Although the class of combed function includes many singular objects such
as the delta ``function'' and at least some locally non-integrable
functions, the generalized functions within the set have a significant
collection of common properties that considerably simplifies their
handling. Note that this is a large set of objects including many singular
ones of common use in physics, since combed function can be
non-differentiable, discontinuous, and may diverge to infinity at singular
points, which may or may not be integrable ones. For the purposes of this
section let us limit ourselves to the case in which the combed generalized
functions are integrable. This will make it easier for us to list their
main common properties, most of which have been demonstrated before. The
detailed extension of these properties to the complete set of combed
generalized functions is therefore postponed to some future opportunity.
- To start with, combed functions have no finite-spike singularities.
In fact, any pathologies that do not have a definite non-zero effect on
the integral of the function, such as finite discontinuities on a
zero-measure subset of the domain, are simply eliminated by the
application of the low-pass filter.
- Since it is the
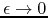 limit of a filtered function, every
combed function assumes at every given point the value given by the
average of the two lateral limits of the original function to that
point, so long as these limits exist,
limit of a filtered function, every
combed function assumes at every given point the value given by the
average of the two lateral limits of the original function to that
point, so long as these limits exist,
where
which in particular holds at all isolated discontinuities where the two
lateral limits exist. Note that, since in the neighborhoods at the two
sides of 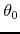 , where
, where 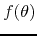 is continuous, the
is continuous, the
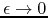 limit of
limit of
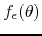 reproduces
reproduces 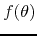 , these two
lateral limits of
, these two
lateral limits of 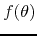 coincide with the two corresponding
lateral limits of
coincide with the two corresponding
lateral limits of
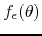 in the
in the 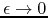 limit.
limit.
- Every combed function
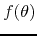 has a well-defined and unique
sequence of Taylor-Fourier coefficients, from which it can be recovered
strictly everywhere within its domain of definition. From the
sequence of Taylor-Fourier coefficients one can always construct the
corresponding inner analytic function
has a well-defined and unique
sequence of Taylor-Fourier coefficients, from which it can be recovered
strictly everywhere within its domain of definition. From the
sequence of Taylor-Fourier coefficients one can always construct the
corresponding inner analytic function 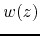 . The combed real function
is always given by the
. The combed real function
is always given by the 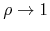 limit of the real part of its
corresponding inner analytic function,
limit of the real part of its
corresponding inner analytic function,
everywhere within that domain, even if the Fourier series of that real
function diverges everywhere.
- If the Fourier series of a combed function converges at all, then it
converges to that combed function everywhere in its domain of
definition.
- If the Fourier series of a combed function diverges, and so long as
there is at most a finite number of dominant singularities of the
corresponding inner analytic function on the unit circle, as they were
defined in [2], it is possible to devise other expressions
involving trigonometric series that converge to the real function, and
that do so as fast as one may wish. We call these alternative
trigonometric series ``center series'', and the algorithm to construct
them is explained in [2].
- Every combed function is the smoothest member of the class of
zero-measure equivalent functions that it belongs to, as was discussed
in Appendix C of [4]. Given another member of that class,
which is therefore a ragged function, there is no difficulty in
``combing'' it, that is in finding the combed function from which it
differs only by a zero-measure function.
- A ragged function can be combed by any one of the following methods:
application to it of the low-pass filter in the
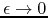 limit;
construction of its Fourier series, if convergent, and therefore of the
limiting function of that series; construction of an expression
containing an alternative trigonometric series, if the Fourier series
fails to converge, and therefore of the limiting function of that
alternative series; construction of its inner-analytic function and
therefore of the limit of the real part of that complex function to the
unit circle.
limit;
construction of its Fourier series, if convergent, and therefore of the
limiting function of that series; construction of an expression
containing an alternative trigonometric series, if the Fourier series
fails to converge, and therefore of the limiting function of that
alternative series; construction of its inner-analytic function and
therefore of the limit of the real part of that complex function to the
unit circle.
In any given setting, if one limits the set of relevant real functions to
be discussed to combed generalized functions, then the use of the very
characteristic ``almost everywhere'' arguments in the harmonic analysis of
the functions become more sparse and better focused on the relevant
features of the functions. The possible exceptional points of the ``almost
everywhere'' arguments become only those singular points on the unit
circle that are brought about by the construction of the corresponding
inner analytic functions.
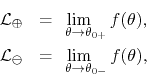
![]() , where
, where ![]() is continuous, the
is continuous, the
![]() limit of
limit of
![]() reproduces
reproduces ![]() , these two
lateral limits of
, these two
lateral limits of ![]() coincide with the two corresponding
lateral limits of
coincide with the two corresponding
lateral limits of
![]() in the
in the ![]() limit.
limit.