Next: Complete Algorithm Up: Up
One of the important quantities one can calculate using the ![]() mean-field method for the polynomial models is the position of the
critical curve within the parameter plane of each model. This is done in
section 3 of chapter 2 of the book [1], for the
case of the
mean-field method for the polynomial models is the position of the
critical curve within the parameter plane of each model. This is done in
section 3 of chapter 2 of the book [1], for the
case of the ![]() model. The result can be extended to the
model. The result can be extended to the
![]() models, and in this general case the
models, and in this general case the ![]() mean-field result for the
critical curve
mean-field result for the
critical curve
![]() of the
of the
![]() polynomial
model is:
polynomial
model is:
which determines
![]() implicitly. Since it is not possible
to solve this equation analytically in order to obtain
implicitly. Since it is not possible
to solve this equation analytically in order to obtain
![]() in explicit form, we will be concerned here with the numerical solution
of this equation, so that we may plot the graph of this function. The
integrals can be written in terms of the parabolic cylinder functions
in explicit form, we will be concerned here with the numerical solution
of this equation, so that we may plot the graph of this function. The
integrals can be written in terms of the parabolic cylinder functions
![]() [3],
[3],
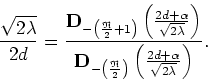
However, this does not help us to solve the equation numerically because
these functions are not readily available in a computer implementation.
Note that for even
![]() the integrals can be written as integrals on a
variable
the integrals can be written as integrals on a
variable
![]() ,
,
![\begin{displaymath}
\frac{\mathfrak{N}}{2d}=\frac{\displaystyle \int_{0}^{\infty...
...1} \;e^{-\left[(d+\alpha/2)\chi
+(\lambda/4)\chi^{2}\right]}}.
\end{displaymath}](img11.gif)
Hence it is not surprising that for even ![]() they can be written in
terms of the error function, which can in fact be done through the
they can be written in
terms of the error function, which can in fact be done through the ![]() functions, with integer
functions, with integer ![]() . The
. The ![]() functions can be
written in terms of the error function
functions can be
written in terms of the error function ![]() , which is given
by [4]
, which is given
by [4]
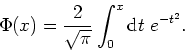
For the first few functions ![]() we
have [5]
we
have [5]
![\begin{eqnarray*}
{\bf D}_{0}(x) & = & e^{-x^{2}/4} {\bf D}_{-1}(x) & = &
\sq...
...)\left[1-\Phi\left(\frac{x}{\sqrt{2}}\right)\right] \right\} \\
\end{eqnarray*}](img17.gif)
From the first two one can get all the functions in this sequence by repeated use of the recurrence relation [6]
which can also be written in the form
Using all this one can solve the equation numerically for the case of
even ![]() , one case at a time, using the error functions erf or
derf, which are readily available for use with the g77
Fortran compiler. For example, for
, one case at a time, using the error functions erf or
derf, which are readily available for use with the g77
Fortran compiler. For example, for
![]() , which is the simplest case,
the equation is
, which is the simplest case,
the equation is
![\begin{displaymath}
\sqrt{\frac{2}{\pi}}\;e^{-\frac{(2d+\alpha)^{2}}{4\lambda}}=...
...t[1-\Phi\left(\frac{2d+\alpha}{2\sqrt{\lambda}}\right)\right].
\end{displaymath}](img21.gif)
Given a value of ![]() , one can solve this equation numerically for
, one can solve this equation numerically for
![]() , and vice-versa. However, this solves only the even-
, and vice-versa. However, this solves only the even-![]() cases,
not the odd-
cases,
not the odd-![]() cases, including
cases, including
![]() .
.
For all values of ![]() one can make a change of variables in order to
simplify the original integrals in a way that is convenient for numerical
purposes. Since the solution for
one can make a change of variables in order to
simplify the original integrals in a way that is convenient for numerical
purposes. Since the solution for ![]() is obviously
is obviously ![]() , we
can assume that
, we
can assume that ![]() and consider the variable
and consider the variable ![]() given by
given by
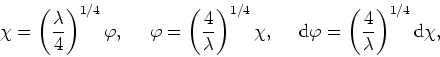
in terms of which the equation becomes
![\begin{displaymath}
\frac{\mathfrak{N}}{2d}=\frac{2}{\sqrt{\lambda}}\;\frac{\dis...
...ft[\frac{2d+\alpha}{\sqrt{\lambda}}\chi^{2}+\chi^{4}\right]}}.
\end{displaymath}](img30.gif)
Defining now a new parameter ![]() given by
given by
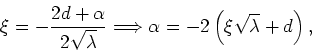
we may write the equation in the form
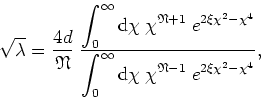
or, multiplying above and below by
![]() ,
,
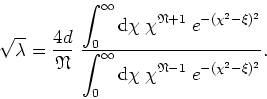
Given a value of ![]() , this allows one to calculate
, this allows one to calculate
![]() using a single pair of numerical integrations, and afterward to calculate
the corresponding
using a single pair of numerical integrations, and afterward to calculate
the corresponding ![]() from
from ![]() ,
, ![]() and
and
![]() . The
parameter
. The
parameter ![]() is a new parameter for the critical curve. In order to
determine its range of variation as we travel along the curve from end to
end, consider first the asymptotic line of the critical curve, for large
values of
is a new parameter for the critical curve. In order to
determine its range of variation as we travel along the curve from end to
end, consider first the asymptotic line of the critical curve, for large
values of ![]() and
and ![]() , which can be obtained through the
representation of the equation in terms of the parabolic cylinder
functions [7], and is given by
, which can be obtained through the
representation of the equation in terms of the parabolic cylinder
functions [7], and is given by
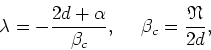
where ![]() is the critical point of the sigma model over the arc
at infinity. In this case we have for
is the critical point of the sigma model over the arc
at infinity. In this case we have for ![]() the expression
the expression
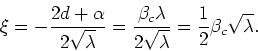
Therefore
![]() corresponds to
corresponds to
![]() and hence to the sigma-model critical point
over the arc at infinity, and when
and hence to the sigma-model critical point
over the arc at infinity, and when
If we now consider the tangent to the critical curve at the Gaussian
point, which can be obtained by differentiating
equation (1) implicitly with respect to ![]() and
and ![]() , then expressing the resulting integrals in terms of the
, then expressing the resulting integrals in terms of the
![]() function [8], and which is
given by
function [8], and which is
given by
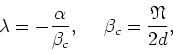
we see that in this case we get for ![]() the expression
the expression
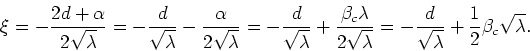
Therefore
![]() corresponds to
corresponds to
![]() and hence to the Gaussian point, and when
and hence to the Gaussian point, and when
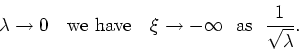
In short, we have the following limiting behaviors:
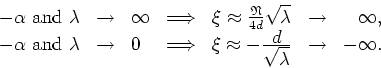
We have therefore the following general algorithm for the numerical solution of the equation:
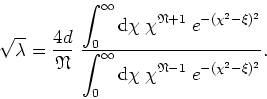
The resulting pair
![]() is a point of the critical curve of
the
is a point of the critical curve of
the
![]() model, in
model, in ![]() dimensions. Probably the best way to choose
values of
dimensions. Probably the best way to choose
values of ![]() so that the resulting points
so that the resulting points
![]() are
distributed fairly homogeneously along the critical curve is to use the
equation of the tangent line at the Gaussian point, choosing some
are
distributed fairly homogeneously along the critical curve is to use the
equation of the tangent line at the Gaussian point, choosing some
![]() , integer values of
, integer values of
![]() , and using
, and using
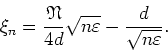
Since the functions being integrated are centered around a single maximum
that moves to large values of the variable when ![]() is large, in order
to integrate them efficiently we must know the location of the points of
maximum of the functions. The basic idea for the integration of one of
these functions is to start at the point of maximum of the function, and
then to integrate to both sides, down towards zero and up towards
infinity. Let us consider then the functions
is large, in order
to integrate them efficiently we must know the location of the points of
maximum of the functions. The basic idea for the integration of one of
these functions is to start at the point of maximum of the function, and
then to integrate to both sides, down towards zero and up towards
infinity. Let us consider then the functions
where ![]() is an integer. Except for the case
is an integer. Except for the case ![]() this is zero for
this is zero for
![]() , and in all cases for
, and in all cases for
![]() . Taking the
derivative we get
. Taking the
derivative we get
Besides vanishing at ![]() (for
(for ![]() ) and at
) and at ![]() , which are clearly
points of minimum, this can be zero for
, which are clearly
points of minimum, this can be zero for
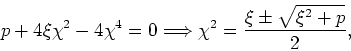
and since
![]() only the
only the ![]() sign can be kept, and we get
sign can be kept, and we get
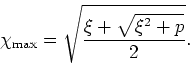
This is correct in all cases including ![]() . For
. For ![]() we have that, if
we have that, if
![]() , then
, then
![]() , and if
, and if ![]() , then
, then
![]() . Note that the only case in which the maximum is at
zero is
. Note that the only case in which the maximum is at
zero is ![]() with
with ![]() , in all other cases the maximum is at a
positive and non-vanishing value of
, in all other cases the maximum is at a
positive and non-vanishing value of ![]() .
.
The functions examined above have the form of a pulse around their points
of maximum, but this pulse has a variable width, which decreases as the
parameter ![]() increases to positive values. This makes is harder to
find an appropriate numerical integration interval for them. For the
cases
increases to positive values. This makes is harder to
find an appropriate numerical integration interval for them. For the
cases ![]() we can perform one more transformation of the integrals, in
order to improve this situation. We make a transformation of integration
variables to the variable
we can perform one more transformation of the integrals, in
order to improve this situation. We make a transformation of integration
variables to the variable
![]() and hence write
and hence write
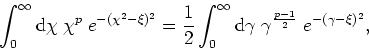
where the integrand has now a fairly constant width around its maximum.
In this case the location of the point of maximum is a bit different,
that is,
![]() is not exactly
is not exactly
![]() . The
integrand is now
. The
integrand is now
and its derivative is given by
![\begin{displaymath}
\left[\frac{p-1}{2}\gamma^{\frac{p-3}{2}}
-2(\gamma-\xi)\gamma^{\frac{p-1}{2}}\right]e^{-(\gamma-\xi)^{2}}.
\end{displaymath}](img81.gif)
Note that, due to the possibly negative powers of ![]() , the cases
, the cases
![]() and
and ![]() should be examined separately. For
should be examined separately. For ![]() we have
we have
which is zero at the point of minimum at infinity and at ![]() ,
which is therefore the point of maximum. Since
,
which is therefore the point of maximum. Since ![]() this is
valid only for
this is
valid only for ![]() , for
, for ![]() the function is monotonically
decreasing with its maximum at
the function is monotonically
decreasing with its maximum at ![]() . For
. For ![]() we have
we have
![\begin{displaymath}
\left[\frac{1}{2}\gamma^{-\frac{1}{2}}
-2(\gamma-\xi)\gamma^{\frac{1}{2}}\right]e^{-(\gamma-\xi)^{2}}.
\end{displaymath}](img91.gif)
Note that in this case the function has an infinite derivative at the
point ![]() , which makes it unsuitable for numerical integration.
Its point of maximum can be obtained as one of the roots of a quadratic
polynomial and is in fact included in the general case, which we proceed
to analyze. If we multiply it by
, which makes it unsuitable for numerical integration.
Its point of maximum can be obtained as one of the roots of a quadratic
polynomial and is in fact included in the general case, which we proceed
to analyze. If we multiply it by ![]() , the derivative of the
general case becomes
, the derivative of the
general case becomes
![\begin{displaymath}
\gamma^{\frac{p}{2}}
\left[\frac{p-1}{2}-2(\gamma-\xi)\gamma\right]e^{-(\gamma-\xi)^{2}}.
\end{displaymath}](img93.gif)
Except for the cases ![]() and
and ![]() this vanishes at the points of
minimum at
this vanishes at the points of
minimum at ![]() and at
and at
![]() , and for all cases
it vanishes at the point of maximum given by
, and for all cases
it vanishes at the point of maximum given by
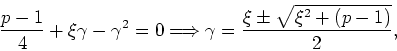
where since ![]() only the
only the ![]() sign can be kept, and we get
sign can be kept, and we get
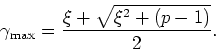
This is in fact correct in all cases including ![]() and
and ![]() . For
. For ![]() we see that this gives the correct answer: if
we see that this gives the correct answer: if ![]() , then
, then
![]() , and if
, and if ![]() , then
, then
![]() . Note that the
only case in which the maximum is at zero is
. Note that the
only case in which the maximum is at zero is ![]() with
with ![]() , in
all other cases the maximum is at a positive and non-vanishing value of
, in
all other cases the maximum is at a positive and non-vanishing value of
![]() .
.