Next: Fortran Routines Up: Numerical Solution for the Previous: Numerical Solution for the
Let us record here the complete algorithm, with all the details. Recall
that the integrals in the ![]() variable should not be used in the
cases
variable should not be used in the
cases ![]() and
and ![]() , in which cases we should use the integrals in
terms of the variable
, in which cases we should use the integrals in
terms of the variable ![]() . For all other values of
. For all other values of ![]() we should use
the integrals in terms of the variable
we should use
the integrals in terms of the variable ![]() for ease of numerical
integration.
for ease of numerical
integration.
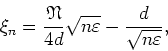
where ![]() is a very rough estimate of the corresponding value
of
is a very rough estimate of the corresponding value
of ![]() . For example, for
. For example, for
![]() using
using
![]() and
and ![]() up
to
up
to ![]() results on
results on ![]() up to approximately
up to approximately ![]() , and using
, and using
![]() and
and ![]() up to
up to ![]() results on
results on ![]() up to
approximately
up to
approximately ![]() .
.
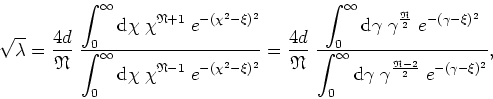
where the integrals in ![]() and in
and in ![]() are related by
are related by
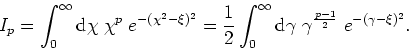
The form of the integral to be used depends on the value of ![]() :
:
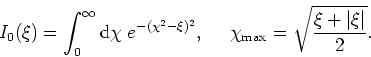
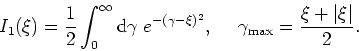
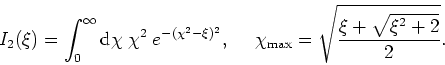
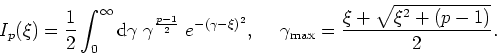
The integration is to be by cubic splines, in which the integration
increment ![]() for a function
for a function ![]() with derivative
with derivative ![]() , from
a point
, from
a point ![]() to a point
to a point ![]() , is given by
, is given by
where
![]() ,
,
![]() , and so on. The
functions involved and their derivatives are
, and so on. The
functions involved and their derivatives are
![\begin{eqnarray*}
f_{p}(\chi) & = & \chi^{p}\;e^{-(\chi^{2}-\xi)^{2}}, g_{p}(...
...rac{p-1}{2}+2\xi\gamma
-2\gamma^{2}\right]e^{-(\gamma-\xi)^{2}}.
\end{eqnarray*}](img121.gif)
This completes the algorithm. One should also recall that for even ![]() the relevant integrals, with odd
the relevant integrals, with odd ![]() , can be written in terms of the
error function. In particular, for
, can be written in terms of the
error function. In particular, for
![]() one can use
one can use
![\begin{eqnarray*}
I_{1}(\xi) & = & \frac{\sqrt{\pi}}{4}\;[1+\Phi(\xi)], I_{3}...
...ac{\sqrt{\pi}}{4}\;\xi\;[1+\Phi(\xi)]+\frac{1}{4}\;e^{-\xi^{2}}.
\end{eqnarray*}](img122.gif)
This can be used to solve the problem in this case, probably in a more
efficient way. For larger even values of ![]() one has to derive the
corresponding relations for each case in order to do this.
one has to derive the
corresponding relations for each case in order to do this.