Next: Bibliography Up: Appendix: Examples of Use Previous: Potential in a Rectangular
Consider the two-dimensional cross-section of an infinite solid cylinder
made of a heat-conducting material. Suppose that its two sides are in
contact with heat baths, one above and one below, as shown in
Figure 5. The system reaches a state of stationary heat
conduction given by Laplace equation in cylindrical coordinates for the
temperature ![]() ,
,
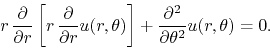
The two boundary values are shown in the illustration. In the standard (and simpler) formulation of the problem, one considers that the two heat baths are thermally isolated from each other, but the thermally isolating material needed to accomplish this is not taken into account explicitly. The solution of the problem can be given in terms of mixed power and Fourier series for the static temperature and for the radial and angular components of the heat flux density, which is related to the gradient of the temperature,
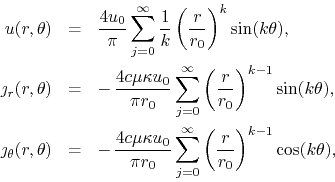
where ![]() and the constants appearing in
and the constants appearing in
![]() and
and
![]() characterize the material. Note that so long
as
characterize the material. Note that so long
as ![]() all the series are strongly convergent to
all the series are strongly convergent to ![]() functions, due to the exponential decay with
functions, due to the exponential decay with ![]() of the factors involving
the ratio
of the factors involving
the ratio ![]() . However, at the surface of the cylinder, for
. However, at the surface of the cylinder, for
![]() , the series for the temperature is not absolutely or uniformly
convergent, but only point-wise convergent. Besides, at this surface the
series for the components of the heat flux density are simply everywhere
divergent. This is caused by the neglect to take into account the
necessity to have a layer of isolating material of finite thickness
between the two heat baths, which causes the presence of infinite heat
fluxes at the points where these two heat baths are infinitely close to
each other, and connected to each other through the material of the
cylinder.
, the series for the temperature is not absolutely or uniformly
convergent, but only point-wise convergent. Besides, at this surface the
series for the components of the heat flux density are simply everywhere
divergent. This is caused by the neglect to take into account the
necessity to have a layer of isolating material of finite thickness
between the two heat baths, which causes the presence of infinite heat
fluxes at the points where these two heat baths are infinitely close to
each other, and connected to each other through the material of the
cylinder.
One can change this by applying the first-order linear low-pass filter to
the boundary condition at the surface of the cylinder, with a small
angular range parameter ![]() . This exchanges the two discontinuities
of the boundary temperature for two thin layers with steep variation of
the temperature, as shown in Figure 6. Since the coefficients of
the differential equation do not depend on
. This exchanges the two discontinuities
of the boundary temperature for two thin layers with steep variation of
the temperature, as shown in Figure 6. Since the coefficients of
the differential equation do not depend on ![]() , we may write at once
the filtered solution, by simply plugging the filter factor
, we may write at once
the filtered solution, by simply plugging the filter factor
![]() into the series,
into the series,
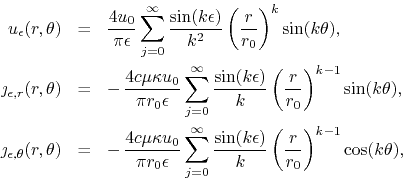
where ![]() . The series for the temperature is now absolutely and
uniformly convergent everywhere, and the series for the components of the
heat flux density are point-wise convergent almost everywhere at the
surface of the cylinder. If we write for example the components
. The series for the temperature is now absolutely and
uniformly convergent everywhere, and the series for the components of the
heat flux density are point-wise convergent almost everywhere at the
surface of the cylinder. If we write for example the components
![]() at the surface, we get
at the surface, we get
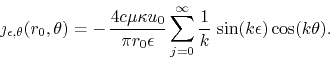
One can show that this series is convergent everywhere using trigonometric identities to write it in the form
![\begin{displaymath}
\jmath_{\epsilon,\theta}(r_{0},\theta)
=
\frac{2c\mu\kapp...
...in[k(\theta-\epsilon)]
-
\sin[k(\theta+\epsilon)]
\right\}.
\end{displaymath}](img237.png)
The two sine series obtained in this way have coefficients that converge monotonically to zero and therefore are convergent by the Dirichlet test, or alternatively by the monotonicity criterion discussed in [3]. The other field component at the surface can be analyzed in a similar way. It is given by
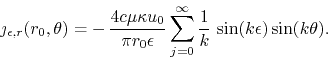
In this case the analysis with the monotonicity criterion shown that the
series is convergent at all points except four, the points
![]() ,
,
![]() and
and
![]() .
Further application of the first-order filter, or the application of the
second-order filter, can then be used to further improve the situation.
.
Further application of the first-order filter, or the application of the
second-order filter, can then be used to further improve the situation.
We can say that the introduction of the filter in fact improved the
representation of the physical system in this problem, from the physical
standpoint, because the two steep variations of the temperature can be
understood as representations of the temperature within two thin slices of
a thermally insulating material, of angular thickness ![]() ,
inserted between the two heath baths. Once again we see that the
introduction of the filter brought the description of the physical system
closer to reality.
,
inserted between the two heath baths. Once again we see that the
introduction of the filter brought the description of the physical system
closer to reality.
Just an in the previous example, the remaining points of divergence are in
the component of the heat flux density normal to the surface, exactly at
the point where we have the material interfaces between the heat baths and
the thermally insulating material of the thin slices. This once more
suggests that these remaining divergences are related to the imperfect
representation of these material interfaces. Therefore it seems
appropriate to use once more the first-order filter on the boundary
condition, with a range parameter
![]() which could go
all the way down to the molecular scale.
which could go
all the way down to the molecular scale.
Although a direct and detailed physical interpretation seems not to be
immediately apparent in this case, essentially the same comments made in
the last example about the role of a second application of the filter are
also true in this case. Clearly it will have the effect of smoothing out
the sharp transitions between the two materials. Regardless of the value
of the parameter ![]() , it will certainly render all the series
absolutely and uniformly convergent everywhere, since they will then all
have at least a factor of
, it will certainly render all the series
absolutely and uniformly convergent everywhere, since they will then all
have at least a factor of ![]() in their coefficients.
in their coefficients.
Note that since the derivation of the heat equation from fundamental physical principles has a statistical character, involving averages over large numbers of molecules of the material involved, it is not unreasonable that one may meet with difficulties in its description of nature when one goes down to the molecular scale, as we have done here. We may interpret these isolated singularities as consequences of the use of a physical theory at the very edge of its recognized domain of validity.