Introduction

One of the many important uses of Fourier series is in the role of tools for the solution of boundary value problems involving partial differential equations in Cartesian or cylindrical coordinates [1]. From a historical point of view, one may say that this is, in fact, the original use of these series. In this type of application the final solution of the boundary value problem is obtained in the form of a Fourier series, and the real function that gives its coefficients is not immediately available in closed form. This is not surprising, since the determination of the function is the very essence of the boundary value problem. It is often necessary to take derivatives of the solutions obtained, in order to calculate physical quantities of relevance within the applications, and in some cases the term-wise differentiation of the Fourier series obtained for the solution results in a divergent series.

This is usually brought about by overly simplified initial conditions or boundary conditions, which are used when formulating the physical problem in order to simplify the sequence of operations leading to the solution in the form of a Fourier series. Common cases in which this can happen are the calculation of the acceleration in problems with the vibrating string, the calculation of the electric field in problems involving the electrostatic potential within a box and the calculation of the heat flux density in problems involving the heat equation in solids. Some simple examples on these lines are examined briefly in Appendix B, in order to illustrate the main points of this paper.

In this paper we show that certain low-pass filters can be used to deal with such situations in a way that changes the mathematics so as to make the relevant Fourier series converge, while at the same time changing nothing of importance in the physics involved. The first-order linear low-pass filter is defined in precise mathematical terms, and several of its main properties are established, both on the real line and within a periodic interval. The first-order filter is then used to define higher-order filters, the use of which not only results in convergent Fourier series, but in series that also converge faster and to smoother functions, allowing one to take a few term-by-term derivatives, as needed within the applications involved.

Although the concept of a low-pass filter originates from an engineering practice, it can be defined theoretically in precise mathematical terms, as an operation on real functions. In fact, all the linear low-pass filters discussed here can be understood as integral operators acting in the space of integrable real functions. They can be expressed by integrals on the real line, involving certain kernel functions. They can be defined both on the whole real line and within a periodic interval such as $[-\pi ,\pi ]$, which allows one to write Fourier expansions for the real functions, in the form

$$f(x) = \frac{1}{2}\, \alpha_{0} + \sum_{k=1}^{\infty} \left[ \alpha_{k}\cos(kx) + \beta_{k}\sin(kx) \right],$$

where the coefficients are given by

$$\begin{eqnarray*} \alpha_{k} & = & \frac{1}{\pi} \int_{-\pi}^{\pi}dx\, \cos... ..._{k} & = & \frac{1}{\pi} \int_{-\pi}^{\pi}dx\, \sin(kx)f(x). \end{eqnarray*}$$

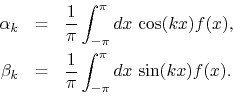
Since boundary value problems typically involve partial differential equations within compact domains, it is of particular importance to determine the action of the low-pass filters on functions defined on compact intervals. We will also establish how the filters act directly on the Fourier representations of these functions.