Standard Model

The four-component $SO(4)$ model has an important application in the Standard Model of high-energy elementary particles. The field component $\varphi_{\mathfrak{N}}(n_{\mu})$ corresponds in this case to the Higgs field. In this application the continuum limit must be taken from the broken-symmetric phase, for it is essential that we have, in the limit, a non-zero $V_{0}$ due to spontaneous symmetry breaking.

It is certainly possible to take limits from the broken-symmetric phase to the critical line in such a way that either $V_{0}$ or $m_{\mathfrak{N}}$ has a finite and non-zero limit. It is not so obvious, but true in $d=4$, that one can take limits in which both are simultaneously finite and non-zero. In fact, the calculations imply that in this case there is a definite relation between $V_{0}$ and $m_{\mathfrak{N}}$.

If we recall our results for $v_{0}$ and $\alpha_{\mathfrak{N}}$ in the broken-symmetric phase (Equations (7) and (13)), without external sources, we have

$$\begin{eqnarray*} \lambda v_{0}^{2} & = & - \left[ \alpha + \lambda (\m... ... \alpha + \lambda (\mathfrak{N}+2) \sigma_{0}^{2} \right]. \end{eqnarray*}$$

It immediately follows that we have the following result relating $v_{0}$ and $\alpha_{\mathfrak{N}}$,

$$2\lambda v_{0}^{2} = \alpha_{\mathfrak{N}}.$$

Writing this in terms of dimensionfull quantities we get

$$2\lambda a^{d-4} V_{0}^{2} = m_{\mathfrak{N}}^{2}.$$

Of course the important dimension here is $d=4$, but let us comment on the other cases anyway. In $d=3$ we are forced once again to make $\lambda\to 0$, which takes us to the Gaussian point, and if we do this at the appropriate pace, we then simply get $2\Lambda V_{0}^{2}=m_{\mathfrak{N}}^{2}$. In $d=5$ we conclude that, so long as $\lambda$ and $V_{0}$ are finite, we must have $m_{\mathfrak{N}}=0$. If we insist on a finite and non-zero $m_{\mathfrak{N}}$, then $V_{0}$ must diverge to infinity. So in this case we cannot take a limit in such a way that both $V_{0}$ and $m_{\mathfrak{N}}$ remain finite and non-zero.

However, in $d=4$, and only in $d=4$, we get a definite relation between $V_{0}$ and $m_{\mathfrak{N}}$, involving only the dimensionless parameters of the model, and valid for all allowed values of these parameters within the broken-symmetric phase, given by

$$\frac{V_{0}}{m_{\mathfrak{N}}} = \frac{1}{\sqrt{2\lambda}}.$$

Since the values of $V_{0}$ and $m_{\mathfrak{N}}$ are known experimentally, namely $V_{0}\approx 246$ Gev and $m_{\mathfrak{N}}\approx 126$ Gev, we immediately get a result for $\lambda$,

$$\lambda \approx 0.131.$$

Given this result, we can find $\alpha$ as well. All we have to do is to use the equation of the critical line, given in Equation (8),

$$\alpha + \lambda (\mathfrak{N}+2) \sigma_{0}^{2} = 0,$$

with $\mathfrak {N}=4$ and our best numerical evaluation of $\sigma_{0}^{2}$ for $d=4$, which is $\sigma_{0}^{2}\approx 0.15493$, and we get

$$\alpha \approx -0.122.$$

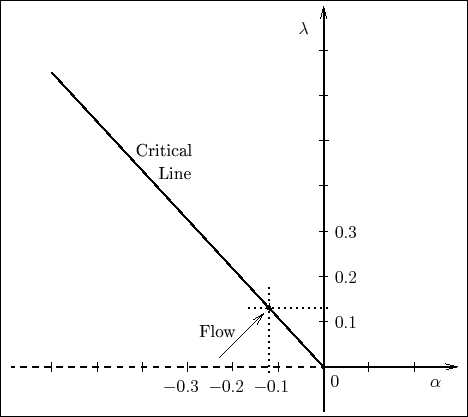
Conceptually, this is a rather remarkable result. Please observe that we are not using the experimental data to make statements about expectation values, but instead to determine the values of bare dimensionless parameters within the mathematical structure of the model. We are able, using the experimental data, to pinpoint the location in the parameter space of the model, along the critical line, where it must be located if it is applicable to the real world,

$$(\alpha,\lambda) \approx (-0.122,0.131).$$

This is a point at a distance of approximately $0.179$ from the Gaussian point, along the critical line, which makes an angle of approximately $47.0$ degrees with the negative $\alpha$ semi-axis. The situation in the parameter-plane of the model is depicted in Figure 1, which is drawn approximately to scale.

Figure 1: Critical diagram of the model in $d=4$, for $\mathfrak {N}=4$, with the Standard Model continuum limit point $(\alpha ,\lambda )\approx (-0.122,0.131)$ singled out, showing the path of a possible continuum limit flow.

One may wonder how accurate this result may be. In the Standard Model there are electroweak charges associated to $\vec{\varphi}(n_{\mu})$, which are being ignored here. It is of course possible that these other interactions might change the expectation value and the renormalized mass of the Higgs field. However, after the symmetry is broken and the three Goldstone bosons $\varphi_{i}(n_{\mu})$, $i=1,2,3$ are absorbed by the three massive vector bosons, the single remaining scalar field which is the Higgs has no electromagnetic charge, and undergoes only weak interactions, if any. Therefore it is reasonable to think that whatever corrections there may be to the result above are probably quite small. By comparison to possible weak perturbative corrections, the results presented here have a rather brutal character, since they handle correctly the non-perturbative phenomenon of spontaneous symmetry breaking, at the quantum level, flipping the sign of $\alpha$ to negative values in that process.