Another Regular Sine Series with Odd $k$

Consider the Fourier series of a periodic function built with segments of quadratic functions, joined together so that the resulting function is continuous and differentiable. As is well known it is given by the sine series

$$S_{\rm s} = \frac{32}{\pi^{3}} \sum_{j=0}^{\infty} \frac{1}{(2j+1)^{3}}\, \sin[(2j+1)\theta].$$

The corresponding FC series is then

$$\bar{S}_{\rm s} = \frac{32}{\pi^{3}} \sum_{j=0}^{\infty} \frac{1}{(2j+1)^{3}}\, \cos[(2j+1)\theta].$$

Note that due to the factors of $1/k^{3}$ (with $k=2j+1$), these series are already absolutely and uniformly convergent. But we will proceed with the construction in any case. The complex $S_{v}$ series is given by

$$S_{v} = \frac{32}{\pi^{3}} \sum_{j=0}^{\infty} \frac{1}{(2j+1)^{3}}\, v^{2j+1},$$

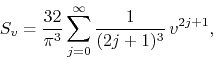
and the complex power series $S_{z}$ is given by

$$S_{z} = \frac{32}{\pi^{3}} \sum_{j=0}^{\infty} \frac{1}{(2j+1)^{3}}\, z^{2j+1}.$$

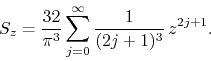
The ratio test tells us that the disk of convergence of $S_{z}$ is the unit disk. If we consider the inner analytic function $w(z)$ within this disk we observe that $w(0)=0$, as expected. We have for this function

$$w(z) = \frac{32}{\pi^{3}} \sum_{j=0}^{\infty} \frac{1}{(2j+1)^{3}}\, z^{2j+1}.$$

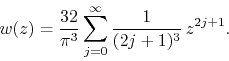
Being given by a monotonic series of step $2$ this function has two dominant singularities, located at $z=1$ and at $z=-1$, as one can easily verify by taking its second logarithmic derivative, which is proportional to the inner analytic function of the standard square wave, that we examined before in Subsection B.2,

$$\begin{eqnarray*} z\, \frac{dw(z)}{dz} & = & \frac{32}{\pi^{3}} \sum_{j=0}^... ...c{32}{\pi^{3}} \sum_{j=0}^{\infty} \frac{1}{2j+1}\, z^{2j+1}. \end{eqnarray*}$$

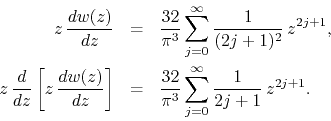
We must therefore use the two factors $(z-1)(z+1)=z^{2}-1$ in the construction of the center series,

$$\begin{eqnarray*} C_{z} & = & \frac{32}{\pi^{3}} \left(z^{2}-1\right) \sum_... ... \frac{24j^{2}+2}{\left(4j^{2}-1\right)^{3}}\, z^{2j} \right]. \end{eqnarray*}$$

Unlike the original series, with coefficients that behave as $1/k^{3}$ (with $k=2j+1$), this series has coefficients that go to zero as $1/k^{4}$ when $k\to\infty$, and therefore converges faster than the original one. This shows, in particular, that our evaluation of the set of dominant singularities of $w(z)$ was in fact correct. We have therefore for $S_{z}$ the representation

$$S_{z} = \frac{32}{\pi^{3}}\, \frac{z}{z^{2}-1} \left[ ... ...frac{24j^{2}+2}{\left(4j^{2}-1\right)^{3}}\, z^{2j} \right],$$

with the singularities factored out. Although both this series and the original one are absolutely and uniformly convergent, this converges faster, and may be differentiated twice, still resulting in other series that are also absolutely and uniformly convergent.

We may now take the real and imaginary parts of the $S_{v}$ series in order to obtain faster-converging representation of the original DP Fourier series and its FC series. We have on the unit circle, as we saw before in Subsection B.2,

$$\frac{z}{z^{2}-1} = \frac{-\mbox{\boldmath$\imath$}}{2\sin(\theta)},$$

and therefore

$$\begin{eqnarray*} S_{v} & = & \frac{16}{\pi^{3}}\, \frac{-\mbox{\boldmath$\i... ...4j^{2}+2}{\left(4j^{2}-1\right)^{3}}\, \cos(2j\theta) \right]. \end{eqnarray*}$$

The original DP function is given by the imaginary part,

$$f_{\rm s}(\theta) = \frac{16}{\pi^{3}\sin(\theta)} \left... ...^{2}+2}{\left(4j^{2}-1\right)^{3}}\, \cos(2j\theta) \right],$$

and the corresponding FC function $f_{\rm c}(\theta)=\bar{f}_{\rm s}(\theta)$ is given by the real part,

$$f_{\rm c}(\theta) = \frac{16}{\pi^{3}\sin(\theta)} \left... ...^{2}+2}{\left(4j^{2}-1\right)^{3}}\, \sin(2j\theta) \right].$$

Both of these series converge faster than the original Fourier series.