Next: Strong Convergence Up: Some Basic Convergence Results Previous: Some Basic Convergence Results
In order to discuss this case we must go all the way back to the case of plain DP trigonometric series, without any consideration of whether or not they are Fourier series. Hence, let us suppose that we have an arbitrary pair of FC trigonometric series,
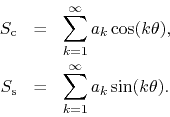
Without any further assumptions, we may then construct the complex series
![]() and
and ![]() ,
,
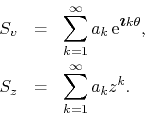
Let us suppose that ![]() fails to converge at a single point
fails to converge at a single point ![]() located strictly inside the open unit disk. Then it follows from the
basic convergence theorem that it cannot converge at any point outside the
circle centered at zero with its boundary going through the point
located strictly inside the open unit disk. Then it follows from the
basic convergence theorem that it cannot converge at any point outside the
circle centered at zero with its boundary going through the point ![]() .
This is so because, if the series did converge at some point outside this
disk, them by that theorem it would converge everywhere in a larger disk,
which contains the point of divergence
.
This is so because, if the series did converge at some point outside this
disk, them by that theorem it would converge everywhere in a larger disk,
which contains the point of divergence ![]() . This is absurd, and
therefore we conclude that the series must be divergent at all points
strictly outside the closed disk defined by the point of divergence
. This is absurd, and
therefore we conclude that the series must be divergent at all points
strictly outside the closed disk defined by the point of divergence
![]() .
.
It follows therefore that in this case the ![]() series is divergent
everywhere over the whole unit circle. The same is then true for
series is divergent
everywhere over the whole unit circle. The same is then true for ![]() ,
of course, and similar conclusions may be drawn for the associated DP
trigonometric series. Note that while the convergence of
,
of course, and similar conclusions may be drawn for the associated DP
trigonometric series. Note that while the convergence of ![]() at a
given point implies the convergence of both
at a
given point implies the convergence of both ![]() and
and ![]() at
that point, the lack of convergence of
at
that point, the lack of convergence of ![]() implies only that at least
one of the two DP trigonometric series diverges. The other one might still
converge. We may immediately conclude that at least one of the two series
in the FC pair is divergent. But in fact, one can see that both must be
divergent almost everywhere, by the following argument.
implies only that at least
one of the two DP trigonometric series diverges. The other one might still
converge. We may immediately conclude that at least one of the two series
in the FC pair is divergent. But in fact, one can see that both must be
divergent almost everywhere, by the following argument.
If we consider the absolute value of the terms of ![]() at
at ![]() , we
have
, we
have
![]() , where
, where
![]() and
and ![]() . Since
. Since ![]() is divergent at
is divergent at
![]() ,
,
![]() cannot go to zero faster than
cannot go to zero faster than ![]() ,
because a limit to zero as
,
because a limit to zero as
![]() with any strictly
positive
with any strictly
positive ![]() would be sufficient for the series of the absolute
values of the terms of
would be sufficient for the series of the absolute
values of the terms of ![]() to converge, since in this case it can be
bounded from above by a convergent asymptotic integral, as is shown in
Section B.1 of Appendix B. This would imply
that
to converge, since in this case it can be
bounded from above by a convergent asymptotic integral, as is shown in
Section B.1 of Appendix B. This would imply
that ![]() is absolutely convergent and hence convergent, which is
absurd. This means that we must have
is absolutely convergent and hence convergent, which is
absurd. This means that we must have
for ![]() and some minimum value
and some minimum value ![]() of
of ![]() . In other words,
. In other words,
![]() must in fact diverge to infinity exponentially with
must in fact diverge to infinity exponentially with ![]() , in fact
just about as fast as
, in fact
just about as fast as
![]() , which goes to infinity as
, which goes to infinity as
![]() since
since ![]() . Since these coefficients are those of
both
. Since these coefficients are those of
both ![]() and
and ![]() , and a limit of the coefficients to zero
as
, and a limit of the coefficients to zero
as ![]() is a necessary condition for convergence, both these
series must diverge almost everywhere, that is, everywhere except possibly
for a few special points, such as the sine series at
is a necessary condition for convergence, both these
series must diverge almost everywhere, that is, everywhere except possibly
for a few special points, such as the sine series at ![]() .
.
Therefore, in this case there are no trigonometric series at all that
converge almost everywhere on the unit circle. We say that such series are
divergent almost everywhere. Besides, since any Fourier series is a
particular case of trigonometric series, in this case there are no
almost-everywhere convergent Fourier series as well. This is true whenever
the maximum disk of convergence of ![]() around
around ![]() is smaller than
the open unit disk, which also means that the function
is smaller than
the open unit disk, which also means that the function ![]() to which
to which
![]() converges must have at least one singularity strictly within that
disk.
converges must have at least one singularity strictly within that
disk.
In conclusion, given any DP trigonometric series, be it a Fourier series
or not, if the power series built from its coefficients is divergent
anywhere strictly within the unit disk, then the trigonometric series is
divergent almost everywhere in the periodic interval. The same follows if
it can be verified that the function ![]() has a singularity strictly
within the open unit disk. We refer to this situation as one of strong
divergence.
has a singularity strictly
within the open unit disk. We refer to this situation as one of strong
divergence.
Note that in this case we cannot assert whether or not the trigonometric
series is a Fourier series. In this case it is not possible to take any
limit from the interior of the maximum disk of convergence to the unit
circle, which becomes disconnected from the analytic region of the ![]() series. In fact, it is an interesting question whether or not, in this
situation, any real functions can exist that give the coefficients of the
trigonometric series by means of the usual integrals. While a negative
answer to this question seems to be compelling, for now we must leave this
here as a simple conjecture.
series. In fact, it is an interesting question whether or not, in this
situation, any real functions can exist that give the coefficients of the
trigonometric series by means of the usual integrals. While a negative
answer to this question seems to be compelling, for now we must leave this
here as a simple conjecture.