Next: About the Ratio Test Up: Appendix: Technical Proofs Previous: Appendix: Technical Proofs
It is not a difficult task to establish the absolute and uniform
convergence of a complex power series on a circle centered at the origin,
or the lack thereof, starting from the behavior of the terms of the series
in the limit ![]() , if we assume that they behave as inverse powers
of
, if we assume that they behave as inverse powers
of ![]() for large values of
for large values of ![]() . If we have a complex power series
. If we have a complex power series ![]() with coefficients
with coefficients ![]() , at a point
, at a point ![]() strictly inside the unit
disk,
strictly inside the unit
disk,
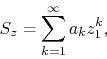
where
![]() and
and ![]() , then it is absolutely
convergent if and only if the series
, then it is absolutely
convergent if and only if the series
![]() of the absolute
values of the coefficients,
of the absolute
values of the coefficients,
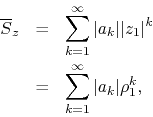
converges. One can show that this sum will be finite if, for ![]() above a
certain minimum value
above a
certain minimum value ![]() , it holds that
, it holds that
for some positive real constant ![]() and some real constant
and some real constant
![]() . This is true because the sum of a finite set of initial
terms is necessarily finite, and because in this case we may bound the
remaining infinite sum from above by a convergent asymptotic integral,
. This is true because the sum of a finite set of initial
terms is necessarily finite, and because in this case we may bound the
remaining infinite sum from above by a convergent asymptotic integral,
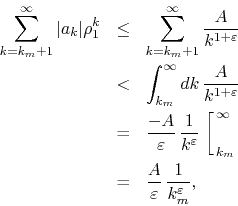
as illustrated in Figure 1. In that illustration each
vertical rectangle has base ![]() and height given by
and height given by
![]() ,
and therefore area given by
,
and therefore area given by
![]() . As one can see, the
construction is such that the set of all such rectangles is below the
graph of the function
. As one can see, the
construction is such that the set of all such rectangles is below the
graph of the function
![]() , and therefore the sum of
their areas is contained within the area under that graph, to the right of
, and therefore the sum of
their areas is contained within the area under that graph, to the right of
![]() . This establishes the necessary inequality between the sum and the
integral.
. This establishes the necessary inequality between the sum and the
integral.
So long as ![]() is not zero, this establishes an upper bound to a
sum of positive quantities, which is therefore a monotonically increasing
sum. It then follows from the well-known theorem of real analysis that the
sum necessarily converges, and therefore the series
is not zero, this establishes an upper bound to a
sum of positive quantities, which is therefore a monotonically increasing
sum. It then follows from the well-known theorem of real analysis that the
sum necessarily converges, and therefore the series ![]() is absolutely
convergent at
is absolutely
convergent at ![]() .
.
In addition to this, one can see that the convergence condition does not
depend on ![]() , since that dependence is only within the complex
variable
, since that dependence is only within the complex
variable
![]() , and vanishes when we take absolute
values. This implies uniform convergence because, given a strictly
positive real number
, and vanishes when we take absolute
values. This implies uniform convergence because, given a strictly
positive real number ![]() , absolute convergence for this value of
, absolute convergence for this value of
![]() implies convergence for this same value of
implies convergence for this same value of ![]() , with the
same solution
, with the
same solution ![]() for the convergence condition. This makes it
clear that the solution of the convergence condition for
for the convergence condition. This makes it
clear that the solution of the convergence condition for ![]() is
independent of position and therefore that the series is also uniformly
convergent on the circle of radius
is
independent of position and therefore that the series is also uniformly
convergent on the circle of radius ![]() centered at the origin.
centered at the origin.
This establishes a sufficient condition for the absolute and uniform
convergence of the complex power series on the circle. On the other hand,
if we have that, for ![]() above a certain minimum value
above a certain minimum value ![]() ,
,
with positive real ![]() and real
and real
![]() , then it is possible
to bound the sum
, then it is possible
to bound the sum
![]() from below by an asymptotic integral
that diverges to positive infinity. This is done in a way similar to the
one used for the establishment of the upper bound, but inverting the
situation so as to keep the area under the graph contained within the
combined areas of the rectangles, as illustrated in Figure 2.
The argument then establishes in this case that, for
from below by an asymptotic integral
that diverges to positive infinity. This is done in a way similar to the
one used for the establishment of the upper bound, but inverting the
situation so as to keep the area under the graph contained within the
combined areas of the rectangles, as illustrated in Figure 2.
The argument then establishes in this case that, for ![]()
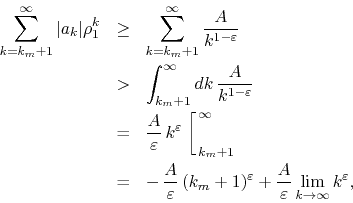
and therefore that
![]() diverges to infinity. A similar
calculation can be performed in the case
diverges to infinity. A similar
calculation can be performed in the case ![]() , leading to
logarithms and yielding the same conclusions. This does not prove or
disprove convergence itself, but it does establish the absence of absolute
convergence. It also shows that, so long as
, leading to
logarithms and yielding the same conclusions. This does not prove or
disprove convergence itself, but it does establish the absence of absolute
convergence. It also shows that, so long as
![]() behaves
as a power of
behaves
as a power of ![]() for large
for large ![]() , the previous condition is both sufficient
and necessary for absolute convergence.
, the previous condition is both sufficient
and necessary for absolute convergence.