Next: Appendix: Examples of Limits Up: Appendix: Technical Proofs Previous: Evaluations of Convergence
Let us show that the Taylor series of an analytic function cannot satisfy
the ratio test at the boundary of its maximum convergence disk. We will
assume that the convergence disk is the open unit disk, but the proof can
be easily generalized. It the series satisfies the test, then it follows
that there is a strictly positive real number ![]() and an integer
and an integer ![]() such that, for all
such that, for all ![]() we have
we have
We observe now that since ![]() over the whole unit circle, this
condition is in fact independent of the angular position and valid over
the whole unit circle, so that we have
over the whole unit circle, this
condition is in fact independent of the angular position and valid over
the whole unit circle, so that we have
Now, consider a point ![]() given by any value of
given by any value of ![]() and the value
and the value
for the radius. Since ![]() is strictly positive and strictly smaller than
one, we have that
is strictly positive and strictly smaller than
one, we have that
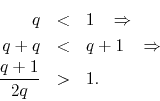
It follows therefore that the point ![]() is strictly outside the unit
disk. We consider now the ratio test for this new point. We start from the
known valid condition on the unit disk, so that we have
is strictly outside the unit
disk. We consider now the ratio test for this new point. We start from the
known valid condition on the unit disk, so that we have
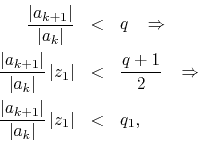
which establishes the upper bound ![]() . Besides, since we know that
. Besides, since we know that ![]() is strictly less than one, we also have that
is strictly less than one, we also have that
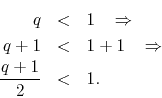
What we have concluded here is that ![]() , and therefore we conclude
that the series satisfies the ratio test at the new point, which is
strictly outside the unit disk, and hence converges there. Therefore, the
basic convergence theorem implies that the maximum disk of convergence of
the series
, and therefore we conclude
that the series satisfies the ratio test at the new point, which is
strictly outside the unit disk, and hence converges there. Therefore, the
basic convergence theorem implies that the maximum disk of convergence of
the series ![]() extends beyond the unit circle. This contradicts the
hypothesis that the open unit disk is the maximum disk of convergence, and
we conclude therefore that the series cannot satisfy the ratio test at the
boundary of its maximum disk of convergence.
extends beyond the unit circle. This contradicts the
hypothesis that the open unit disk is the maximum disk of convergence, and
we conclude therefore that the series cannot satisfy the ratio test at the
boundary of its maximum disk of convergence.
Another way to interpret this result is to say that, if the Taylor series
![]() does satisfy the ratio test at the boundary of a given disk, then
that disk is not its maximum disk of convergence. It follows therefore
that the maximum disk of convergence is larger than the given disk, and
contains it.
does satisfy the ratio test at the boundary of a given disk, then
that disk is not its maximum disk of convergence. It follows therefore
that the maximum disk of convergence is larger than the given disk, and
contains it.