Next: Conclusions and Outlook Up: Extension of the Schwarzschild Previous: Final Component Equation
Let us now show and briefly discuss some sample results obtained by means
of a numerical computer program written to calculate the solution for
![]() , so as to confirm the existence of solutions, as well as to
confirm and display some of the main properties of the solutions, in order
to illustrate their general behavior in a qualitative and visual way. A
full description and discussion of the numerical solution, as well as of
the properties of the solutions, will be given in a separate paper, which
is forthcoming. This will include a detailed analysis of the
, so as to confirm the existence of solutions, as well as to
confirm and display some of the main properties of the solutions, in order
to illustrate their general behavior in a qualitative and visual way. A
full description and discussion of the numerical solution, as well as of
the properties of the solutions, will be given in a separate paper, which
is forthcoming. This will include a detailed analysis of the
![]() black-hole limit.
black-hole limit.
In the graphs shown in Figures 4 to 6 one can see
results for ![]() (solid line),
(solid line), ![]() (dashed line) and
(dashed line) and
![]() (dotted line) for several runs of a program written to solve
Equation (86). The program used to plot these graphs
employed the Runge-Kutta fourth-order integration algorithm, running in
quadruple-precision mode, that is, in double-precision mode on a
(dotted line) for several runs of a program written to solve
Equation (86). The program used to plot these graphs
employed the Runge-Kutta fourth-order integration algorithm, running in
quadruple-precision mode, that is, in double-precision mode on a ![]() -bit
machine, with a self-adjustable increment for
-bit
machine, with a self-adjustable increment for ![]() , and about
, and about ![]() plotting points. The most relevant physical data in each case is reported
within each graph, such as the value of
plotting points. The most relevant physical data in each case is reported
within each graph, such as the value of ![]() and the value of
and the value of
![]() . The graph in Figure 4 exemplifies the low
energy-density regime, the one in Figure 5 the middle
energy-density regime, and that in Figure 6 the high
energy-density regime.
. The graph in Figure 4 exemplifies the low
energy-density regime, the one in Figure 5 the middle
energy-density regime, and that in Figure 6 the high
energy-density regime.
 |
In two of these graphs, those in Figures 5 and 6, a
rendering of the identity function is included (dash-dotted line), for
comparison with ![]() . Since the difference
. Since the difference
![]() appears in the denominator of the factor
appears in the denominator of the factor
![]() that
multiplies the term
that
multiplies the term ![]() in the invariant interval, the proximity
between the two corresponding curves tells us how close we are to having a
singularity in that factor. The critical point
in the invariant interval, the proximity
between the two corresponding curves tells us how close we are to having a
singularity in that factor. The critical point ![]() is the point of
greatest proximity between
is the point of
greatest proximity between ![]() and
and ![]() and thus indicates
approximately where the corresponding event horizon would form, if and
when that was the case. The critical point is also the point of minimum of
the difference
and thus indicates
approximately where the corresponding event horizon would form, if and
when that was the case. The critical point is also the point of minimum of
the difference
![]() , which seems to be always positive, as
one would expect.
, which seems to be always positive, as
one would expect.
 |
Due to the rather large values either set or obtained for some of these
quantities, in the graphs shown in Figures 5 and 6 the
curves for ![]() and
and ![]() are normalized so that the maximum
value of their amplitudes become
are normalized so that the maximum
value of their amplitudes become ![]() . For the same reason, in the graph in
Figure 6 the negative part of the data for
. For the same reason, in the graph in
Figure 6 the negative part of the data for ![]() is
given in a logarithmic scale, using base-
is
given in a logarithmic scale, using base-![]() logs. What is actually
plotted is the quantity
logs. What is actually
plotted is the quantity
![]() . This means that the
negative part of the curve for
. This means that the
negative part of the curve for ![]() in this graph has much larger
absolute values than is immediately apparent. All the other parts of the
curves shown are on a linear scale, including the positive part of the
curve for
in this graph has much larger
absolute values than is immediately apparent. All the other parts of the
curves shown are on a linear scale, including the positive part of the
curve for ![]() .
.
 |
The basic qualitative behavior of both the function ![]() and the
function
and the
function ![]() is thus confirmed by the numerical analysis. The
limits both for
is thus confirmed by the numerical analysis. The
limits both for ![]() and for
and for ![]() behave just as was
predicted by our previous analysis. In particular, the Schwarzschild
solution is indeed the
behave just as was
predicted by our previous analysis. In particular, the Schwarzschild
solution is indeed the ![]() asymptotic limit of our solutions
here, thus indicating that the matter is indeed localized, and in most
cases quite strongly so, with an apparent exponential decay of the energy
density for large values of
asymptotic limit of our solutions
here, thus indicating that the matter is indeed localized, and in most
cases quite strongly so, with an apparent exponential decay of the energy
density for large values of ![]() . The fact that
. The fact that ![]() and hence
and hence
![]() can become negative and large has important consequences. The
fact that they become negative seems to be a general feature of all the
solutions worked out so far. Once
can become negative and large has important consequences. The
fact that they become negative seems to be a general feature of all the
solutions worked out so far. Once ![]() and hence
and hence ![]() become negative, the metric factor
become negative, the metric factor
![]() becomes
becomes
| (106) |
which goes towards zero as
![]() increases. Note that, once
increases. Note that, once
![]() becomes negative, there is no longer any possibility of this
factor having a singularity like the one at
becomes negative, there is no longer any possibility of this
factor having a singularity like the one at ![]() in the Schwarzschild
solution. When
in the Schwarzschild
solution. When
![]() , we have for the physical element
of length
, we have for the physical element
of length ![]() in the radial direction
in the radial direction
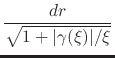 |
|||
| (107) |
When ![]() we have that
we have that ![]() tends to some possibly large
but finite negative value, so that we actually have that
tends to some possibly large
but finite negative value, so that we actually have that
| (108) |
which means that
| (109) |
The numerical data seems to indicate that, in the situations in which
![]() is close to zero at the critical point, the
quantity
is close to zero at the critical point, the
quantity ![]() seems to tend to become very large for smaller
non-zero values of
seems to tend to become very large for smaller
non-zero values of ![]() , so that the radial lengths are significantly
shrunk in most of the interior of the fluid matter distribution. The data
seems to be consistent with the situation in which, in the limit in which
we make
, so that the radial lengths are significantly
shrunk in most of the interior of the fluid matter distribution. The data
seems to be consistent with the situation in which, in the limit in which
we make
![]() , we have that
, we have that
![]() , and also that
, and also that
![]() linearly with
linearly with ![]() . In fact, it seems that we also have that
. In fact, it seems that we also have that
| (110) |
for all values of ![]() smaller than
smaller than ![]() , so that in this limit the
radial lengths shrink all the way to zero in most of the interior of the
region containing the matter. In this way, the approach to a black-hole
configuration seems to be tied up with a complete shrinkage of most of the
volume of the region where the fluid matter is located. Note that, due to
the shrinking of the radial lengths, below the value
, so that in this limit the
radial lengths shrink all the way to zero in most of the interior of the
region containing the matter. In this way, the approach to a black-hole
configuration seems to be tied up with a complete shrinkage of most of the
volume of the region where the fluid matter is located. Note that, due to
the shrinking of the radial lengths, below the value ![]() of
of ![]() there is no possibility of working out an illustrative isometric embedding
such as the one we worked out for the Schwarzschild solution, shown in
Figure 1.
there is no possibility of working out an illustrative isometric embedding
such as the one we worked out for the Schwarzschild solution, shown in
Figure 1.
In such circumstances the geometry within the region containing the fluid matter distribution does have some rather odd characteristics indeed, since the radial lengths shrink while the angular lengths at the same position do not change at all. In essence, this is what makes the embedding just mentioned impossible. Since it suffices for one of the lengths involved do decrease in order for the volume to decrease, this radial shrinkage does cause the volume to shrink under the fluid matter distribution. Note that, although the angular lengths do not change, they cease to be anything close to geodesics of the spatial geometry. One can always go from any point to any other point within the region containing the fluid matter distribution through only radial displacements, going from the first point to the center and from the center to the second point. With enough radial shrinkage, the distance traversed in this way will be smaller than that of a path between the two points that involves angular displacements. If the radial lengths shrink all the way to zero, then the geodesic distances between any two points in the shrunk region are zero. In effect, it is as if all the points in that region become effectively the same point.
According to the numerical data, the larger the value of ![]() ,
where
,
where ![]() is the position of the inflection point of
is the position of the inflection point of ![]() ,
the closer to a singularity of
,
the closer to a singularity of
![]() at the critical point,
where
at the critical point,
where
![]() , we get. But so far indications are
that one never actually gets to such a singular solution for finite values
of
, we get. But so far indications are
that one never actually gets to such a singular solution for finite values
of ![]() . The larger the value of
. The larger the value of ![]() , the closer
, the closer
![]() will be to the radial position
will be to the radial position ![]() of the sphere that contains
essentially all the fluid matter, coming from within. In the cases which
are closer to exhibiting a singularity of
of the sphere that contains
essentially all the fluid matter, coming from within. In the cases which
are closer to exhibiting a singularity of
![]() , and
therefore closer to the formation of a black hole with an event horizon,
the remaining internal volume seems to be highly concentrated near the
surface of the matter distribution, while the radial lengths seem to
shrink to zero somewhat faster for smaller values of
, and
therefore closer to the formation of a black hole with an event horizon,
the remaining internal volume seems to be highly concentrated near the
surface of the matter distribution, while the radial lengths seem to
shrink to zero somewhat faster for smaller values of ![]() . In fact, under
these conditions the energy density seems to develop a large and narrow
peak near that surface, as can be seen in some cases, if one recalls that
. In fact, under
these conditions the energy density seems to develop a large and narrow
peak near that surface, as can be seen in some cases, if one recalls that
![]() is closely related to the energy density. All these
issues will be described and examined in detail in the aforementioned
forthcoming paper.
is closely related to the energy density. All these
issues will be described and examined in detail in the aforementioned
forthcoming paper.
The case ![]() corresponds to ``fluid matter'' in the form of pure
radiation, and it is interesting that even in this case, so long as
corresponds to ``fluid matter'' in the form of pure
radiation, and it is interesting that even in this case, so long as
![]() is large enough, we do still obtain static solutions, in
which the fluid matter is still strongly localized. Of course, at least in
part this is being allowed by the fact that we are ignoring losses of
energy by outward radiation from the surface of the matter distribution, a
more detailed treatment of which would certainly lead to non-static
solutions. However, if we are close to a configuration that has a
singularity of
is large enough, we do still obtain static solutions, in
which the fluid matter is still strongly localized. Of course, at least in
part this is being allowed by the fact that we are ignoring losses of
energy by outward radiation from the surface of the matter distribution, a
more detailed treatment of which would certainly lead to non-static
solutions. However, if we are close to a configuration that has a
singularity of
![]() at the critical point, where
at the critical point, where
![]() , then the strong red shift effect for any
outward radiation from the vicinity of the spherical surface at that
radial position will tend to make such energy losses very small, and then
our static solution may still be a fair approximation of reality.
, then the strong red shift effect for any
outward radiation from the vicinity of the spherical surface at that
radial position will tend to make such energy losses very small, and then
our static solution may still be a fair approximation of reality.