Consistency Condition

In this section we calculate this consistency condition for the specific case of time independence and spherical symmetry. In other words, we now write explicitly, under these conditions, the expression that is given in Equation (14) of the text. The energy-momentum tensor in Equation (13) of the text, in its mixed form, can be written symbolically in the following way,

$$T_{\mu}^{\nu}(r) = \delta_{\mu}^{0}\delta_{0}^{\nu}T_{0}(... ...2}^{\nu}T_{2}(r) + \delta_{\mu}^{3}\delta_{3}^{\nu}T_{3}(r).$$ (111)

This symbolic form encodes the fact that $T_{\mu}^{\nu}(r)$ is a diagonal matrix. We may calculate the covariant divergence using this symbolic form of the tensor. In order to do this we first write explicitly the contracted covariant derivative of the mixed tensor $T_{\mu}^{\nu}(r)$ that appears in its covariant divergence,

$$D_{\nu}T_{\mu}^{\nu}(r) = \partial_{\nu} T_{\mu}^{\nu}(r... ...\nu}(r) + \Gamma^{\nu}_{\;\;\nu\alpha} T_{\mu}^{\alpha}(r).$$ (112)

As we will see, the only non-trivial condition that comes from Equation (14) of the text is the one for the case $\mu=1$. However, let us calculate first the general, non-contracted case, of this covariant derivative,

$$D_{\lambda} T_{\mu}^{\nu}(r) = \partial_{\lambda} T_{\m... ...(r) + \Gamma^{\nu}_{\;\;\lambda\alpha} T_{\mu}^{\alpha}(r).$$ (113)

We can do this using the symbolic form for $T_{\mu}^{\nu}(r)$,

$$D_{\lambda}T_{\mu}^{\nu}(r) = \partial_{\lambda}\! \left[ \delta_{\mu}^{0}\delta_{0}^{\nu}T_{0}... ...2}\delta_{2}^{\nu}T_{2}(r) + \delta_{\mu}^{3}\delta_{3}^{\nu}T_{3}(r) \right] +$$

$$- \Gamma^{\alpha}_{\;\;\lambda\mu} \left[ \delta_{\alpha}^{0}\del... ...delta_{2}^{\nu}T_{2}(r) + \delta_{\alpha}^{3}\delta_{3}^{\nu}T_{3}(r) \right] +$$

$$+ \Gamma^{\nu}_{\;\;\lambda\alpha} \left[ \delta_{\mu}^{0}\delta_... ...elta_{2}^{\alpha}T_{2}(r) + \delta_{\mu}^{3}\delta_{3}^{\alpha}T_{3}(r) \right]$$

$$= \delta_{\mu}^{0}\delta_{0}^{\nu} [\partial_{\lambda}T_{0}(r)] + \... ...bda}T_{2}(r)] + \delta_{\mu}^{3}\delta_{3}^{\nu} [\partial_{\lambda}T_{3}(r)] +$$

$$- \Gamma^{\alpha}_{\;\;\lambda\mu} \delta_{\alpha}^{0}\delta_{0}^... ... \Gamma^{\alpha}_{\;\;\lambda\mu} \delta_{\alpha}^{3}\delta_{3}^{\nu}T_{3}(r) +$$

$$+ \Gamma^{\nu}_{\;\;\lambda\alpha} \delta_{\mu}^{0}\delta_{0}^{\a... ... + \Gamma^{\nu}_{\;\;\lambda\alpha} \delta_{\mu}^{3}\delta_{3}^{\alpha}T_{3}(r)$$

$$= \delta_{\mu}^{0}\delta_{0}^{\nu}\delta_{\lambda}^{1} T'_{0}(r) + ... ...1} T'_{2}(r) + \delta_{\mu}^{3}\delta_{3}^{\nu}\delta_{\lambda}^{1} T'_{3}(r) +$$

$$- \Gamma^{0}_{\;\;\lambda\mu} \delta_{0}^{\nu}T_{0}(r) - \Gamma^{... ...elta_{2}^{\nu}T_{2}(r) - \Gamma^{3}_{\;\;\lambda\mu} \delta_{3}^{\nu}T_{3}(r) +$$

$$+ \Gamma^{\nu}_{\;\;\lambda 0} \delta_{\mu}^{0}T_{0}(r) + \Gamma^... ...elta_{\mu}^{2}T_{2}(r) + \Gamma^{\nu}_{\;\;\lambda 3} \delta_{\mu}^{3}T_{3}(r),$$ (114)

where we have used the fact that, since $T_{\mu}(r)$ are functions of only $r$, we have that

$$\partial_{\lambda}T_{\mu}(r) = \delta_{\lambda}^{1}T'_{\mu}(r),$$ (115)

where the prime indicates derivatives with respect to $r$, just as in the text. If we now contract the indices $\lambda$ and $\nu$ we get

$$D_{\nu}T_{\mu}^{\nu}(r) = \delta_{\mu}^{0}\delta_{0}^{\nu}\delta_{\nu}^{1} T'_{0}(r) + \del... ...u}^{1} T'_{2}(r) + \delta_{\mu}^{3}\delta_{3}^{\nu}\delta_{\nu}^{1} T'_{3}(r) +$$

$$- \Gamma^{0}_{\;\;\nu\mu} \delta_{0}^{\nu}T_{0}(r) - \Gamma^{1}_{... ...} \delta_{2}^{\nu}T_{2}(r) - \Gamma^{3}_{\;\;\nu\mu} \delta_{3}^{\nu}T_{3}(r) +$$

$$+ \Gamma^{\nu}_{\;\;\nu 0} \delta_{\mu}^{0}T_{0}(r) + \Gamma^{\nu... ...2} \delta_{\mu}^{2}T_{2}(r) + \Gamma^{\nu}_{\;\;\nu 3} \delta_{\mu}^{3}T_{3}(r)$$

$$= \delta_{\mu}^{0}\delta_{0}^{1} T'_{0}(r) + \delta_{\mu}^{1}\delta... ..._{\mu}^{2}\delta_{2}^{1} T'_{2}(r) + \delta_{\mu}^{3}\delta_{3}^{1} T'_{3}(r) +$$

$$- \Gamma^{0}_{\;\;0\mu} T_{0}(r) - \Gamma^{1}_{\;\;1\mu} T_{1}(r) - \Gamma^{2}_{\;\;2\mu} T_{2}(r) - \Gamma^{3}_{\;\;3\mu} T_{3}(r) +$$

$$+ \Gamma^{\nu}_{\;\;\nu 0} \delta_{\mu}^{0}T_{0}(r) + \Gamma^{\nu... ...2} \delta_{\mu}^{2}T_{2}(r) + \Gamma^{\nu}_{\;\;\nu 3} \delta_{\mu}^{3}T_{3}(r)$$

$$= \delta_{\mu}^{1} T'_{1}(r) - \Gamma^{0}_{\;\;0\mu} T_{0}(r) - \Ga... ...u} T_{1}(r) - \Gamma^{2}_{\;\;2\mu} T_{2}(r) - \Gamma^{3}_{\;\;3\mu} T_{3}(r) +$$

$$+ \Gamma^{\nu}_{\;\;\nu 0} \delta_{\mu}^{0}T_{0}(r) + \Gamma^{\nu... ...} \delta_{\mu}^{2}T_{2}(r) + \Gamma^{\nu}_{\;\;\nu 3} \delta_{\mu}^{3}T_{3}(r),$$ (116)

since we have that $\delta_{0}^{1}=0$, $\delta_{1}^{1}=1$, $\delta_{2}^{1}=0$ and $\delta_{3}^{1}=0$. We now observe that, from the values of the components of the connection $\Gamma^{\alpha}_{\;\;\mu\nu}$ that were given in Table 1 of the text, we can get the values of the elements that appear in the contractions $\Gamma^{\nu}_{\;\;\nu 0}$, $\Gamma^{\nu}_{\;\;\nu 1}$, $\Gamma^{\nu}_{\;\;\nu 2}$ and $\Gamma^{\nu}_{\;\;\nu 3}$, and in this way we get for these contractions

$$\Gamma^{\nu}_{\;\;\nu 0} = \Gamma^{0}_{\;\;00} + \Gamma^{1}_{\;\;10} + \Gamma^{2}_{\;\;20} + \Gamma^{3}_{\;\;30}$$

$$= 0+0+0+0$$

$$= 0,$$

$$\Gamma^{\nu}_{\;\;\nu 1} = \Gamma^{0}_{\;\;01} + \Gamma^{1}_{\;\;11} + \Gamma^{2}_{\;\;21} + \Gamma^{3}_{\;\;31}$$

$$= \nu'(r)+\lambda'(r)+\frac{1}{r}+\frac{1}{r}$$

$$= \nu'(r)+\lambda'(r)+\frac{2}{r},$$

$$\Gamma^{\nu}_{\;\;\nu 2} = \Gamma^{0}_{\;\;02} + \Gamma^{1}_{\;\;12} + \Gamma^{2}_{\;\;22} + \Gamma^{3}_{\;\;32}$$

$$= 0+0+0+\cot(\theta)$$

$$= \cot(\theta),$$

$$\Gamma^{\nu}_{\;\;\nu 3} = \Gamma^{0}_{\;\;03} + \Gamma^{1}_{\;\;13} + \Gamma^{2}_{\;\;23} + \Gamma^{3}_{\;\;33}$$

$$= 0+0+0+0$$

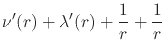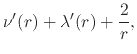$$= 0.$$ (117)

We therefore have for our contracted covariant derivative

$$D_{\nu}T_{\mu}^{\nu}(r) = \delta_{\mu}^{1} T'_{1}(r) - \Gamma^{0}_{\;\;0\mu} T_{0}(r) - \Ga... ...u} T_{1}(r) - \Gamma^{2}_{\;\;2\mu} T_{2}(r) - \Gamma^{3}_{\;\;3\mu} T_{3}(r) +$$

$$+ \left[ \nu'(r)+\lambda'(r)+\frac{2}{r} \right] \delta_{\mu}^{1}T_{1}(r) + \cot(\theta) \delta_{\mu}^{2}T_{2}(r)$$

$$= \delta_{\mu}^{1} T'_{1}(r) - \Gamma^{0}_{\;\;0\mu} T_{0}(r) - \le... ...t[ \nu'(r)+\lambda'(r)+\frac{2}{r} \right] \delta_{\mu}^{1} \right\} T_{1}(r) +$$

$$\hspace{4em} - \left[ \Gamma^{2}_{\;\;2\mu} - \cot(\theta) \delta_{\mu}^{2} \right] T_{2}(r) - \Gamma^{3}_{\;\;3\mu} T_{3}(r).$$ (118)

This must be zero for all values of $\mu$, and therefore we must write out each one of the cases, using once more the values of the components of the connection $\Gamma^{\alpha}_{\;\;\mu\nu}$, shown in Table 1 of the text,

$$D_{\nu}T_{0}^{\nu}(r) = \delta_{0}^{1} T'_{1}(r) - \Gamma^{0}_{\;\;00} T_{0}(r) - \left\{... ...eft[ \nu'(r)+\lambda'(r)+\frac{2}{r} \right] \delta_{0}^{1} \right\} T_{1}(r) +$$

$$\hspace{4em} - \left[ \Gamma^{2}_{\;\;20} - \cot(\theta) \delta_{0}^{2} \right] T_{2}(r) - \Gamma^{3}_{\;\;30} T_{3}(r)$$

$$= - \Gamma^{0}_{\;\;00} T_{0}(r) - \Gamma^{1}_{\;\;10} T_{1}(r) - \Gamma^{2}_{\;\;20} T_{2}(r) - \Gamma^{3}_{\;\;30} T_{3}(r)$$

$$= - 0\times T_{0}(r) - 0\times T_{1}(r) - 0\times T_{2}(r) - 0\times T_{3}(r)$$

$$= 0,$$

$$D_{\nu}T_{1}^{\nu}(r) = \delta_{1}^{1} T'_{1}(r) - \Gamma^{0}_{\;\;01} T_{0}(r) - \left\{... ...eft[ \nu'(r)+\lambda'(r)+\frac{2}{r} \right] \delta_{1}^{1} \right\} T_{1}(r) +$$

$$\hspace{4em} - \left[ \Gamma^{2}_{\;\;21} - \cot(\theta) \delta_{1}^{2} \right] T_{2}(r) - \Gamma^{3}_{\;\;31} T_{3}(r)$$

$$= T'_{1}(r) - \Gamma^{0}_{\;\;01} T_{0}(r) - \left\{ \Gamma^{1}_{\;\;11} - \left[ \nu'(r)+\lambda'(r)+\frac{2}{r} \right] \right\} T_{1}(r) +$$

$$\hspace{15em} - \Gamma^{2}_{\;\;21} T_{2}(r) - \Gamma^{3}_{\;\;31} T_{3}(r)$$

$$= T'_{1}(r) - \nu'(r) T_{0}(r) + \left[ \nu'(r) + \frac{2}{r} \right] T_{1}(r) - \frac{T_{2}(r)}{r} - \frac{T_{3}(r)}{r}$$

$$= T'_{1}(r) - \nu'(r)[T_{0}(r)-T_{1}(r)] + \frac{[2T_{1}(r)-T_{2}(r)-T_{3}(r)]}{r},$$

$$D_{\nu}T_{2}^{\nu}(r) = \delta_{2}^{1} T'_{1}(r) - \Gamma^{0}_{\;\;02} T_{0}(r) - \left\{... ...eft[ \nu'(r)+\lambda'(r)+\frac{2}{r} \right] \delta_{2}^{1} \right\} T_{1}(r) +$$

$$\hspace{4em} - \left[ \Gamma^{2}_{\;\;22} - \cot(\theta) \delta_{2}^{2} \right] T_{2}(r) - \Gamma^{3}_{\;\;32} T_{3}(r)$$

$$= - \Gamma^{0}_{\;\;02} T_{0}(r) - \Gamma^{1}_{\;\;12} T_{1}(r) - \... ...mma^{2}_{\;\;22} - \cot(\theta) \right] T_{2}(r) - \Gamma^{3}_{\;\;32} T_{3}(r)$$

$$= - 0\times T_{0}(r) - 0\times T_{1}(r) + \cot(\theta) T_{2}(r) - \cot(\theta) T_{3}(r)$$

$$= 0,$$

$$D_{\nu}T_{3}^{\nu}(r) = \delta_{3}^{1} T'_{1}(r) - \Gamma^{0}_{\;\;03} T_{0}(r) - \left\{... ...eft[ \nu'(r)+\lambda'(r)+\frac{2}{r} \right] \delta_{3}^{1} \right\} T_{1}(r) +$$

$$\hspace{4em} - \left[ \Gamma^{2}_{\;\;23} - \cot(\theta) \delta_{3}^{2} \right] T_{2}(r) - \Gamma^{3}_{\;\;33} T_{3}(r)$$

$$= - \Gamma^{0}_{\;\;03} T_{0}(r) - \Gamma^{1}_{\;\;13} T_{1}(r) - \Gamma^{2}_{\;\;23} T_{2}(r) - \Gamma^{3}_{\;\;33} T_{3}(r)$$

$$= - 0\times T_{0}(r) - 0\times T_{1}(r) - 0\times T_{2}(r) - 0\times T_{3}(r)$$

$$= 0,$$ (119)

where we used the fact that $T_{2}(r)=T_{3}(r)$ in the third equation above. Thus we see that three of the four consistency conditions $D_{\nu}T_{\mu}^{\nu}(r)=0$, those for $\mu=0$, $\mu=2$ and $\mu=3$, are automatically satisfied. The only non-trivial condition is that given by $D_{\nu}T_{1}^{\nu}(r)=0$, which results in

$$T'_{1}(r) - \nu'(r) [T_{0}(r)-T_{1}(r)] + \frac{[2T_{1}(r)-T_{2}(r)-T_{3}(r)]}{r} = 0,$$ (120)

and which can also be written as

$$\left[r\nu'(r)\right] [T_{0}(r)-T_{1}(r)] = \left[rT'_{1}(r)\right] + [2T_{1}(r)-T_{2}(r)-T_{3}(r)].$$ (121)

This condition, as a condition on $T_{\mu}^{\nu}$, is required to be satisfied if this energy-momentum tensor is to be used in the right-hand side of the Einstein gravitational field equation.