Next: Conclusions and Outlook Up: Complex Analysis of Real Previous: Conformal Transformations and Singularities
The basic idea of the proof of the generalization of the extended
Cauchy-Goursat theorem will be to embed an arbitrarily given integration
contour on the ![]() plane, which must be a simple closed curve but may
or may not be a differentiable curve, into a region bounded by a differentiable simple closed curve, which is then mapped to the unit
circle on the
plane, which must be a simple closed curve but may
or may not be a differentiable curve, into a region bounded by a differentiable simple closed curve, which is then mapped to the unit
circle on the ![]() plane by a conformal transformation. The embedding
will be such that all the isolated integrable singularities on the
original integration contour are mapped onto the unit circle. This will
then allow us to use the extended Cauchy-Goursat theorem for inner
analytic functions within the unit disk, which was established in
Section 3, to prove the generalized version of that theorem.
Therefore, in this section we will prove the following theorem.
plane by a conformal transformation. The embedding
will be such that all the isolated integrable singularities on the
original integration contour are mapped onto the unit circle. This will
then allow us to use the extended Cauchy-Goursat theorem for inner
analytic functions within the unit disk, which was established in
Section 3, to prove the generalized version of that theorem.
Therefore, in this section we will prove the following theorem.
| (24) |
This is the most complete generalization of the extended Cauchy-Goursat theorem that we will consider here, the only relevant limitation being that the number of isolated integrable singularities be finite.
Let ![]() be an analytic function within a closed simple curve
be an analytic function within a closed simple curve
![]() on the
on the ![]() plane, and let the function
plane, and let the function ![]() also be
analytic almost everywhere on
also be
analytic almost everywhere on ![]() , with the exception of a
finite number of isolated integrable singular points. It follows that, due
to Lemmas 1-4, the corresponding function
, with the exception of a
finite number of isolated integrable singular points. It follows that, due
to Lemmas 1-4, the corresponding function
![]() on the
on the ![]() plane will have the same number of
singularities on it, which will also be isolated integrable singular
points. The curve
plane will have the same number of
singularities on it, which will also be isolated integrable singular
points. The curve ![]() may not be differentiable at some points,
including at some of the singular points. We will consider the integral of
may not be differentiable at some points,
including at some of the singular points. We will consider the integral of
![]() over the integration contour
over the integration contour ![]() on the
on the ![]() plane,
which will then, of course, correspond to the integral of
plane,
which will then, of course, correspond to the integral of ![]() over a corresponding integration contour
over a corresponding integration contour ![]() on the
on the ![]() plane,
under the conformal transformation.
plane,
under the conformal transformation.
 |
The proof that follows will depend on the integration contour ![]() being either differentiable or non-differentiable and convex at all
the singular points found on it. However, this is not a true limitation,
because an integration contour that has one of more singular points where
it is non-differentiable and concave can always be decomposed into two or
more integration contours where those same singular points are convex, as
is shown in Figure 5 for an example with three such points. As
one can see, all the three integration contours into which the original
one is decomposed by the cuts shown (dashed lines) are convex at the
singular points. When the three are put together to form once again the
original contour, the integrals over those cuts, which due to their
orientation are traversed once in each direction, cancel out. Therefore,
if the theorem is proven for all contours which are convex at the singular
points, it follows that it in fact holds for all contours, regardless of
whether they are convex or concave at their singular points. We may
therefore limit the proof to contours which are convex at all their
singular points.
being either differentiable or non-differentiable and convex at all
the singular points found on it. However, this is not a true limitation,
because an integration contour that has one of more singular points where
it is non-differentiable and concave can always be decomposed into two or
more integration contours where those same singular points are convex, as
is shown in Figure 5 for an example with three such points. As
one can see, all the three integration contours into which the original
one is decomposed by the cuts shown (dashed lines) are convex at the
singular points. When the three are put together to form once again the
original contour, the integrals over those cuts, which due to their
orientation are traversed once in each direction, cancel out. Therefore,
if the theorem is proven for all contours which are convex at the singular
points, it follows that it in fact holds for all contours, regardless of
whether they are convex or concave at their singular points. We may
therefore limit the proof to contours which are convex at all their
singular points.
Given an integration contour ![]() within which
within which ![]() is
analytic, and on which
is
analytic, and on which ![]() is analytic except for a finite
number of isolated integrable singularities, at all of which the contour
is either differentiable or non-differentiable and convex, we consider now
the construction on the
is analytic except for a finite
number of isolated integrable singularities, at all of which the contour
is either differentiable or non-differentiable and convex, we consider now
the construction on the ![]() plane of a new closed differentiable
simple curve
plane of a new closed differentiable
simple curve ![]() that contains
that contains ![]() . At any points on
. At any points on ![]() where
where
![]() is analytic there is a neighborhood of that point within
which there are no singularities of
is analytic there is a neighborhood of that point within
which there are no singularities of ![]() which are not located
directly on
which are not located
directly on ![]() , whose union forms a strip around
, whose union forms a strip around ![]() . In this
case we make
. In this
case we make ![]() go through these neighborhoods in a differentiable
fashion, outside the interior of
go through these neighborhoods in a differentiable
fashion, outside the interior of ![]() , so that we ensure that no
singularities of
, so that we ensure that no
singularities of ![]() get included on
get included on ![]() or in its
interior, other than those on
or in its
interior, other than those on ![]() . This can be done even at
non-singular points where the integration contour
. This can be done even at
non-singular points where the integration contour ![]() is not
differentiable, in which case we make
is not
differentiable, in which case we make ![]() just go around the point of
non-differentiability of
just go around the point of
non-differentiability of ![]() , in a differentiable fashion, as can be
seen illustrated in Figure 6.
, in a differentiable fashion, as can be
seen illustrated in Figure 6.
 |
At points of ![]() where
where ![]() has an isolated integrable
singularity, since the singularity is isolated, there is also a
neighborhood of the point within which there are no other
singularities of
has an isolated integrable
singularity, since the singularity is isolated, there is also a
neighborhood of the point within which there are no other
singularities of ![]() , which is part of the aforementioned strip
around
, which is part of the aforementioned strip
around ![]() . In this case we make
. In this case we make ![]() go through this neighborhood,
still keeping to the outer side of
go through this neighborhood,
still keeping to the outer side of ![]() , in such a way that the curve
runs over the singular point in a differentiable way, which is
possible because
, in such a way that the curve
runs over the singular point in a differentiable way, which is
possible because ![]() is convex at that singular point, as is
illustrated by the point
is convex at that singular point, as is
illustrated by the point ![]() in Figure 6. The singular point
is one which the curve
in Figure 6. The singular point
is one which the curve ![]() will therefore share with
will therefore share with ![]() , as is
also illustrated by the point
, as is
also illustrated by the point ![]() in Figure 6. At singular
points where
in Figure 6. At singular
points where ![]() is differentiable we simply make
is differentiable we simply make ![]() tangent to
tangent to
![]() at that point, as is illustrated by the point
at that point, as is illustrated by the point ![]() in
Figure 6.
in
Figure 6.
The result of this process, taken all around ![]() and including all the
isolated integrable singularities found on it, is a differentiable simple
curve
and including all the
isolated integrable singularities found on it, is a differentiable simple
curve ![]() which contains
which contains ![]() and the singularities on it, but that
contains no other singularities of
and the singularities on it, but that
contains no other singularities of ![]() , and which shares with
, and which shares with
![]() all the points where the relevant isolated integrable
singularities of
all the points where the relevant isolated integrable
singularities of ![]() are located. Since by construction
are located. Since by construction ![]() is a differentiable closed simple curve, by the Riemann mapping theorem
there exists a conformal transformation
is a differentiable closed simple curve, by the Riemann mapping theorem
there exists a conformal transformation ![]() that maps it from
the unit circle. Therefore, the inverse conformal transformation
that maps it from
the unit circle. Therefore, the inverse conformal transformation
![]() will map all the isolated integrable singular
points on
will map all the isolated integrable singular
points on ![]() to the unit circle
to the unit circle ![]() .
.
Since the interior of ![]() in mapped by the inverse transformation
in mapped by the inverse transformation
![]() onto the open unit disk, it follows that the
integration contour
onto the open unit disk, it follows that the
integration contour ![]() , which is contained in
, which is contained in ![]() , is mapped by
, is mapped by
![]() onto a closed simple integration contour
onto a closed simple integration contour ![]() contained in the unit disk in the
contained in the unit disk in the ![]() plane, which will not be
differentiable if
plane, which will not be
differentiable if ![]() is not, but which is contained within the closed
unit disk, and that touches the unit circle only at each one of the
isolated integrable singular points of
is not, but which is contained within the closed
unit disk, and that touches the unit circle only at each one of the
isolated integrable singular points of ![]() on
on ![]() that
correspond to the singularities of
that
correspond to the singularities of ![]() on
on ![]() .
.
Observe that, since the curve ![]() does not contain any singularities
of
does not contain any singularities
of ![]() in its strict interior, the interior of the curve
in its strict interior, the interior of the curve
![]() , which is the open unit disk, does not contain any singularities
of
, which is the open unit disk, does not contain any singularities
of ![]() . Therefore, according to the definition given
in [#!CAoRFI!#],
. Therefore, according to the definition given
in [#!CAoRFI!#], ![]() is an inner analytic function. If we now
consider the integral of
is an inner analytic function. If we now
consider the integral of ![]() over
over ![]() , it is a very simple
thing to change the integration variable from
, it is a very simple
thing to change the integration variable from ![]() to
to ![]() ,
,
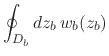 |
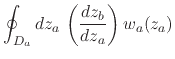 |
||
![$\displaystyle \oint_{D_{a}}dz_{a}\,
\left[
\frac{d\gamma(z_{a})}{dz_{a}}
\right]
w_{a}(z_{a}),$](img96.png) |
(25) |
where we used the relations shown in Equations (14)
and (16). Because ![]() is an analytic
function on the whole closed unit disk, the derivative in brackets is also
an analytic function on the whole closed unit disk, and in addition to
this the function
is an analytic
function on the whole closed unit disk, the derivative in brackets is also
an analytic function on the whole closed unit disk, and in addition to
this the function ![]() is analytic within the integration
contour
is analytic within the integration
contour ![]() and also on
and also on ![]() except for a finite set of isolated
singularities located on the unit circle. By the results of
Lemmas 1-4, these isolated singularity are all
integrable ones. Therefore, since the product of two analytic functions is
also an analytic function, the integrand is analytic within the
integration contour
except for a finite set of isolated
singularities located on the unit circle. By the results of
Lemmas 1-4, these isolated singularity are all
integrable ones. Therefore, since the product of two analytic functions is
also an analytic function, the integrand is analytic within the
integration contour ![]() , and also on it except for a finite set of
isolated integrable singularities on the unit circle, and hence is an
inner analytic function. Therefore, by Theorem 1, that is, the
extended Cauchy-Goursat theorem for inner analytic functions on the unit
disk, the integral is zero, and hence it follows that
, and also on it except for a finite set of
isolated integrable singularities on the unit circle, and hence is an
inner analytic function. Therefore, by Theorem 1, that is, the
extended Cauchy-Goursat theorem for inner analytic functions on the unit
disk, the integral is zero, and hence it follows that
| (26) |
In other words, due to the fact that the integral of ![]() on
on
![]() is zero, which is guaranteed by the extended Cauchy-Goursat
theorem for inner analytic functions, we may conclude that the integral of
is zero, which is guaranteed by the extended Cauchy-Goursat
theorem for inner analytic functions, we may conclude that the integral of
![]() on
on ![]() is also zero. This implies that the extended
Cauchy-Goursat theorem is valid for
is also zero. This implies that the extended
Cauchy-Goursat theorem is valid for ![]() , that is, for arbitrary
complex analytic functions anywhere on the complex plane. This completes
the proof of Theorem 2.
, that is, for arbitrary
complex analytic functions anywhere on the complex plane. This completes
the proof of Theorem 2.
Note that, once we have Theorem 2 established, it is also valid for all inner analytic functions, and therefore automatically includes the contents of Theorem 1, which we may therefore regard as just an intermediate step in the proof.