Next: Generalization to Arbitrary Analytic Up: Complex Analysis of Real Previous: Extension of the Cauchy-Goursat
The validity of the extended version of the Cauchy-Goursat theorem can be
generalized to all complex analytic functions integrated on arbitrarily
given closed integration contours, through the use of conformal
transformations. In order to do this, let us first establish the
definition and the notation for a conformal transformation. This is
essentially a shorter version of the discussion on this topic which was
given in Section 4 of a previous paper [#!CAoRFV!#]. Consider therefore
two complex variables ![]() and
and ![]() and the corresponding complex
planes, a complex analytic function
and the corresponding complex
planes, a complex analytic function ![]() defined on the complex
plane
defined on the complex
plane ![]() with values on the complex plane
with values on the complex plane ![]() , and its inverse
function, which is a complex analytic function
, and its inverse
function, which is a complex analytic function
![]() defined
on the complex plane
defined
on the complex plane ![]() with values on the complex plane
with values on the complex plane ![]() ,
,
| (13) |
Let us point out here that these relations immediately imply that
which in turn imply that
| (15) |
for all pairs of points ![]() and
and ![]() related by the conformal
transformation. This means that any point where the derivative of
related by the conformal
transformation. This means that any point where the derivative of
![]() has a zero on the
has a zero on the ![]() plane corresponds to a point
where the derivative of
plane corresponds to a point
where the derivative of
![]() has a singularity on the
has a singularity on the
![]() plane, and vice-versa.
plane, and vice-versa.
Consider a bounded and simply connected open region ![]() on the complex
plane
on the complex
plane ![]() and its image
and its image ![]() under
under ![]() , which is a similar
region on the complex plane
, which is a similar
region on the complex plane ![]() . It can be shown that if
. It can be shown that if ![]() is analytic on
is analytic on ![]() , is invertible there, and its derivative has no
zeros there, then its inverse function
, is invertible there, and its derivative has no
zeros there, then its inverse function
![]() has these same
three properties on
has these same
three properties on ![]() , and the mapping between the two complex
planes established by
, and the mapping between the two complex
planes established by ![]() and
and
![]() is conformal, in
the sense that it preserves the angles between oriented curves at points
where they cross each other. The famous Riemann mapping theorem
states that such a conformal transformation
is conformal, in
the sense that it preserves the angles between oriented curves at points
where they cross each other. The famous Riemann mapping theorem
states that such a conformal transformation ![]() always exists
between the open unit disk
always exists
between the open unit disk ![]() and any region
and any region ![]() . In addition to
this, these properties of
. In addition to
this, these properties of ![]() and
and
![]() can be
extended to the boundary of the regions so long as these boundaries are
differentiable simple curves.
can be
extended to the boundary of the regions so long as these boundaries are
differentiable simple curves.
Consider therefore that the regions under consideration are the interiors
of simple closed curves. One of these curves will be the unit circle
![]() on the complex plane
on the complex plane ![]() , and the other will be a given closed
differentiable simple curve
, and the other will be a given closed
differentiable simple curve ![]() on the complex plane
on the complex plane ![]() . Since
. Since
![]() , being analytic, is in particular a continuous function,
the image on the
, being analytic, is in particular a continuous function,
the image on the ![]() plane of the unit circle
plane of the unit circle ![]() on the
on the ![]() plane must be a continuous closed curve
plane must be a continuous closed curve ![]() . We can also see that
. We can also see that
![]() must be a simple curve, because the fact that
must be a simple curve, because the fact that ![]() is
invertible on
is
invertible on ![]() means that it cannot have the same value at two
different points of
means that it cannot have the same value at two
different points of ![]() , and therefore no two points of
, and therefore no two points of ![]() can be
the same. Consequently, the curve
can be
the same. Consequently, the curve ![]() cannot self-intersect. Finally,
the fact that
cannot self-intersect. Finally,
the fact that ![]() must be a differentiable curve is a simple
consequence of the facts that the
must be a differentiable curve is a simple
consequence of the facts that the ![]() transformation is
conformal and that the unit circle
transformation is
conformal and that the unit circle ![]() is a differentiable curve.
is a differentiable curve.
Given any analytic function ![]() on the
on the ![]() plane, the
conformal transformation
plane, the
conformal transformation ![]() maps it to a corresponding
function
maps it to a corresponding
function ![]() on the
on the ![]() plane, and the inverse conformal
transformation
plane, and the inverse conformal
transformation
![]() maps that function back to the
function
maps that function back to the
function ![]() on the
on the ![]() plane. We can do this by simply
composing either
plane. We can do this by simply
composing either ![]() or
or ![]() with either the
transformation or its inverse, and simply passing the values of the
functions,
with either the
transformation or its inverse, and simply passing the values of the
functions,
Since the composition of two analytic functions is also an analytic
function, and since ![]() is analytic on the closed unit disk,
whenever
is analytic on the closed unit disk,
whenever ![]() is analytic on the
is analytic on the ![]() plane the corresponding
function
plane the corresponding
function ![]() will also be analytic at the corresponding points
on the
will also be analytic at the corresponding points
on the ![]() plane. Of course, where one of these two functions has an
isolated singularity on its plane of definition, so will the other on the
corresponding point in the other plane. Note that if any of these
functions is integrated over a closed integration contour on which it has
any isolated integrable singularities, whenever these singularities are
branch points we assume that the corresponding branch cuts extend outward from the integration contours.
plane. Of course, where one of these two functions has an
isolated singularity on its plane of definition, so will the other on the
corresponding point in the other plane. Note that if any of these
functions is integrated over a closed integration contour on which it has
any isolated integrable singularities, whenever these singularities are
branch points we assume that the corresponding branch cuts extend outward from the integration contours.
The concepts of a soft singularity and of a borderline hard singularity
can be immediately extended from the case of inner analytic functions
within the unit disk to singularities of arbitrary complex analytic
functions anywhere on the complex plane. The concept of a soft singularity
of ![]() at
at ![]() depends only on the existence of the
depends only on the existence of the ![]() limit of
limit of ![]() . The concept of a hard singularity of
. The concept of a hard singularity of ![]() at
at ![]() depends only on the non-existence of that same limit. Finally, the concept
of a borderline hard singularity can be defined as that of a hard
singularity which is nevertheless an integrable one. In order to discuss
what happens with the singularities under the conformal transformation, we
must establish a few simple preliminary results, by means of the following
lemmas.
depends only on the non-existence of that same limit. Finally, the concept
of a borderline hard singularity can be defined as that of a hard
singularity which is nevertheless an integrable one. In order to discuss
what happens with the singularities under the conformal transformation, we
must establish a few simple preliminary results, by means of the following
lemmas.
Since according to Equations (16) we have that
![]() and since
and since
![]() is analytic within and on the image of
the unit circle by the conformal transformation, if
is analytic within and on the image of
the unit circle by the conformal transformation, if ![]() were
analytic at
were
analytic at ![]() , then
, then ![]() would be analytic at
would be analytic at ![]() ,
because the composition of two analytic functions is also an analytic
function. Therefore, if
,
because the composition of two analytic functions is also an analytic
function. Therefore, if ![]() is singular at
is singular at ![]() , then
, then
![]() must be singular at
must be singular at ![]() . This establishes
Lemma 1.
. This establishes
Lemma 1.
Since according to the definition in Equations (16) we
have that
![]() and since the
and since the
![]() limit on the
limit on the ![]() plane corresponds, through the continuous conformal
transformation, to the
plane corresponds, through the continuous conformal
transformation, to the
![]() limit on the
limit on the ![]() plane, it
follows that if the limit
plane, it
follows that if the limit
| (17) |
exists, then so does the limit
| (18) |
Therefore, if the singularity of ![]() at
at ![]() is a soft
one, which means that the first limit exists, then the singularity of
is a soft
one, which means that the first limit exists, then the singularity of
![]() at
at ![]() is also a soft singularity, since in this case
the second limit also exists. This establishes Lemma 2.
is also a soft singularity, since in this case
the second limit also exists. This establishes Lemma 2.
By an argument similar to the one used in Lemma 2, since
according to the definition in Equations (16) we have
that
![]() , and since the
, and since the
![]() and
and
![]() limits correspond to one another, if
limits correspond to one another, if ![]() is
not well defined at
is
not well defined at ![]() , which means that the limit
, which means that the limit
| (19) |
does not exist, then the limit
| (20) |
also does not exist, and therefore ![]() cannot
be well defined at the corresponding point
cannot
be well defined at the corresponding point ![]() . Therefore, if the
singularity of
. Therefore, if the
singularity of ![]() at
at ![]() is a hard one, then the
singularity of
is a hard one, then the
singularity of ![]() at
at ![]() must also be a hard
singularity. This establishes Lemma 3.
must also be a hard
singularity. This establishes Lemma 3.
If the singularity of ![]() at
at ![]() is an integrable one,
then the integral of
is an integrable one,
then the integral of ![]() along any open integration contour
along any open integration contour
![]() going from a point
going from a point ![]() internal to
internal to ![]() to the singular
point
to the singular
point ![]() ,
,
| (21) |
exists and is a finite complex number. We consider now the corresponding
integral of ![]() along an arbitrary open integration contour
along an arbitrary open integration contour
![]() going from an internal point
going from an internal point ![]() within the open unit disk
to the singular point
within the open unit disk
to the singular point ![]() on the unit circle, and make a
transformation of the integration variable from
on the unit circle, and make a
transformation of the integration variable from ![]() to
to ![]() ,
,
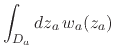 |
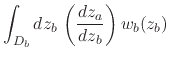 |
||
![$\displaystyle \int_{D_{b}}dz_{b}\,
\left[
\frac{d\gamma^{(-1)}(z_{b})}{dz_{b}}
\right]
w_{b}(z_{b}),$](img90.png) |
(22) |
where we used the relations shown in Equations (14)
and (16), where ![]() is an open integration contour
going from an internal point
is an open integration contour
going from an internal point ![]() to the singular point
to the singular point ![]() ,
and where
,
and where ![]() ,
, ![]() and
and ![]() correspond respectively to
correspond respectively to
![]() ,
, ![]() and
and ![]() , through the conformal transformation.
Since the conformal transformation is an analytic function, the derivative
within brackets is also an analytic function within and on
, through the conformal transformation.
Since the conformal transformation is an analytic function, the derivative
within brackets is also an analytic function within and on ![]() , and
therefore is a limited function there. Since
, and
therefore is a limited function there. Since ![]() by hypothesis
is an integrable function around the singular point
by hypothesis
is an integrable function around the singular point ![]() , and since
the product of a limited function and an integrable function is also an
integrable function, the integrand of this last integral is an integrable
function, and therefore this last integral exists and is a finite complex
number. We thus conclude that
, and since
the product of a limited function and an integrable function is also an
integrable function, the integrand of this last integral is an integrable
function, and therefore this last integral exists and is a finite complex
number. We thus conclude that
| (23) |
exists and is a finite complex number. Therefore, ![]() is an
integrable function around the singular point
is an
integrable function around the singular point ![]() , and therefore
that singularity is also an integrable one. This establishes
Lemma 4.
, and therefore
that singularity is also an integrable one. This establishes
Lemma 4.
We must now consider the question of what is the set of curves ![]() for
which the structure described above can be set up. Given the curve
for
which the structure described above can be set up. Given the curve
![]() , the only additional objects we need in order to do this is the
conformal mapping
, the only additional objects we need in order to do this is the
conformal mapping ![]() and its inverse
and its inverse
![]() ,
between that curve and the unit circle
,
between that curve and the unit circle ![]() , as well as between the
respective interiors. The existence of these transformation functions can
be ensured as a consequence of the Riemann mapping theorem, and of the
associated results relating to conformal mappings between regions of the
complex plane [#!RMPQiu!#]. According to that theorem, a conformal
transformation such as the one we just described exists between any
bounded simply connected open set of the plane and the open unit disk, and
can be extended to the respective boundaries so long as the curve
, as well as between the
respective interiors. The existence of these transformation functions can
be ensured as a consequence of the Riemann mapping theorem, and of the
associated results relating to conformal mappings between regions of the
complex plane [#!RMPQiu!#]. According to that theorem, a conformal
transformation such as the one we just described exists between any
bounded simply connected open set of the plane and the open unit disk, and
can be extended to the respective boundaries so long as the curve ![]() is differentiable. There are therefore no additional limitations on the
differentiable simple closed curves
is differentiable. There are therefore no additional limitations on the
differentiable simple closed curves ![]() that may be considered here.
that may be considered here.