Next: Representation of Non-Integrable Real Up: Complex Analysis of Real Previous: Extended Fourier Theory
In [#!CAoRFI!#] we showed that every integrable real function can be related to a unique inner analytic function that corresponds to it. Since all the inner analytic functions can be organized in integral-differential chains, it follows that each integrable real function can be assigned a unique place in a unique integral-differential chain. However, note that all such functions are assigned only to a part of each one of these chains, the part where the singularities of the inner analytic functions are typically either soft or borderline hard. Still, the complete integral-differential chains do exist and, in particular, do extend indefinitely in the differentiation direction. As we will see, in general non-integrable real functions can be related to inner analytic functions that have one or more hard singularities which are not borderline hard ones, being therefore on the differentiation side of the integral-differential chains.
In addition to this, in [#!CAoRFII!#] we showed that integrable real functions that are piecewise polynomial, and only those, belong to integral-differential chains that have only superpositions of one or more delta ``functions'' and derivatives of delta ``functions'' on their differentiation side, if one goes in the differentiation direction far enough along their integral-differential chains. Therefore, given any integrable real function which is not a piecewise polynomial function, and is such that the corresponding inner analytic function has one or more singularities on the unit circle, a type of real function of which there certainly are many, the integral-differential chain to which it belongs contains, if we travel far enough in the differentiation direction along the chain, real functions which are not integrable at one or more of their singular points.
Starting from an integrable real function ![]() with Fourier
coefficients
with Fourier
coefficients ![]() and
and ![]() , leading to the complex Taylor
coefficients
, leading to the complex Taylor
coefficients ![]() of an inner analytic function
of an inner analytic function ![]() , thus following
the construction presented in [#!CAoRFI!#], it is not difficult to see
from the definition of the angular derivative that after
, thus following
the construction presented in [#!CAoRFI!#], it is not difficult to see
from the definition of the angular derivative that after ![]() angular
differentiations of
angular
differentiations of ![]() we get a proper inner analytic function
we get a proper inner analytic function
![]() with coefficients given by
with coefficients given by
![]() . Starting from the convergent Taylor
series of
. Starting from the convergent Taylor
series of ![]() we have for its
we have for its ![]() angular derivative
angular derivative
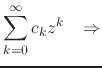 |
|||
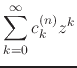 |
|||
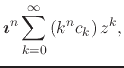 |
(10) |
for
![]() . As we showed in [#!CAoRFI!#], the
coefficients
. As we showed in [#!CAoRFI!#], the
coefficients ![]() associated to an integrable real function
associated to an integrable real function ![]() are limited as functions of
are limited as functions of ![]() . For integrable functions
. For integrable functions ![]() which are not analytic on the whole unit circle the coefficients
which are not analytic on the whole unit circle the coefficients ![]() typically go to zero when
typically go to zero when ![]() , at a pace which is slower than
exponentially fast. We thus see that non-integrable real functions
obtained as derivatives of integrable real functions are associated to
Taylor coefficients which typically diverge to infinity as a positive
power of
, at a pace which is slower than
exponentially fast. We thus see that non-integrable real functions
obtained as derivatives of integrable real functions are associated to
Taylor coefficients which typically diverge to infinity as a positive
power of ![]() in the
in the ![]() limit.
limit.
Therefore, we must conclude that there is a large class of non-integrable
real functions which are still related to corresponding inner analytic
functions such as
![]() , and that can be obtained as the
, and that can be obtained as the
![]() limits to the unit circle of the real parts of these
inner analytic functions. This is the case so long as the
limits to the unit circle of the real parts of these
inner analytic functions. This is the case so long as the
![]() limits of these inner analytic functions exist almost everywhere
on the unit circle. Since angular differentiation conserves the set of
singular points of
limits of these inner analytic functions exist almost everywhere
on the unit circle. Since angular differentiation conserves the set of
singular points of ![]() , at all points where
, at all points where ![]() is analytic, so is
is analytic, so is
![]() , and therefore the limit exists there. Where
, and therefore the limit exists there. Where ![]() has
soft singularities with a large enough degree of softness, namely larger
that or equal to
has
soft singularities with a large enough degree of softness, namely larger
that or equal to ![]() , the angular derivative
, the angular derivative
![]() will also
have soft singularities, and again the limit exists there. Since the
will also
have soft singularities, and again the limit exists there. Since the
![]() limits do not exist at hard singularities, and in
analogy to what we discussed in [#!CAoRFI!#] in the case of the
borderline hard singularities of integrable real functions, we see that we
must impose some limitations on the non-integrable real functions to be
considered here. Specifically, we assume that the numbers of
non-integrable singularities of these functions are finite.
limits do not exist at hard singularities, and in
analogy to what we discussed in [#!CAoRFI!#] in the case of the
borderline hard singularities of integrable real functions, we see that we
must impose some limitations on the non-integrable real functions to be
considered here. Specifically, we assume that the numbers of
non-integrable singularities of these functions are finite.
By the argument above we can immediately determine the existence of many non-integrable real functions which are related to given inner analytic functions. Given any inner analytic function which is not simply a superposition of inner analytic functions associated to singular distributions, and which has one or more singularities on the unit circle, by differentiating it a sufficient number of times we produce an inner analytic function which corresponds to a non-integrable real function. However, given only a non-integrable real function, the problem of the determination of the corresponding inner analytic function is not so immediate. In fact, the problem stated in this way does not really have a unique solution, because such a real function is not really defined on the whole periodic interval, but only on a strict subset of it. The definition of a non-integrable real function must leave out the set of points on the unit circle where it has non-integrable singularities, and thus diverges to infinity. Therefore, one can superpose to such a real function any set of delta ``functions'' and derivatives of delta ``functions'', that have their singularities located at those same singular points, without changing at all the definition of the original non-integrable real function. It then follows that we can add to any inner analytic function that corresponds to the non-integrable real function linear combinations of the inner analytic functions that correspond to the delta ``function'' and to the derivatives of the delta ``function'', which were given explicitly in [#!CAoRFII!#], chosen so that their singularities are located at the points where the non-integrable real function is not defined, without changing the correspondence between the non-integrable real function and the respective inner analytic function.
Let us state, then, the problem we propose to investigate in this paper,
relating to non-integrable real functions and corresponding inner analytic
functions. We want to find out how to determine an inner analytic
function, given only the non-integrable real function, that reproduces
that real function almost everywhere in its domain of definition as the
![]() limit of its real part. We will give here a solution to
this problem for a rather large class of non-integrable real functions, on
which we will impose, however, some limitations. The first limitation will
be, of course, that the real function
limit of its real part. We will give here a solution to
this problem for a rather large class of non-integrable real functions, on
which we will impose, however, some limitations. The first limitation will
be, of course, that the real function ![]() be locally integrable
almost everywhere. This means, in particular, that its number of hard
singular points, either integrable or non-integrable, must be finite. The
other condition is that the non-integrable singular points of
be locally integrable
almost everywhere. This means, in particular, that its number of hard
singular points, either integrable or non-integrable, must be finite. The
other condition is that the non-integrable singular points of ![]() have finite degrees of hardness, as defined and discussed for inner
analytic functions in [#!CAoRFI!#], and translated to real functions in
this paper, at the beginning of Section 2.
have finite degrees of hardness, as defined and discussed for inner
analytic functions in [#!CAoRFI!#], and translated to real functions in
this paper, at the beginning of Section 2.