Singularities of Real Functions

In this paper we will discuss non-integrable real functions, which therefore have on the unit circle hard singularities which are not just borderline hard ones. It is therefore necessary to consider in greater detail the issue of the singularities of real functions. Therefore, let us discuss the translation of the classification of singularities, which has been established in [#!CAoRFI!#] for inner analytic functions in the unit disk of the complex plane, to the case of real functions on the unit circle.

First of all, let us discuss the concept of a removable singularity. This is a well-known concept for analytic functions in the complex plane. What we mean by a removable singularity in the case of real functions on the unit circle is a singular point such that both lateral limits of the function to that point exist and result in the same finite real value, but where the function has been arbitrarily defined to have some other finite real value. This is therefore a point were the function can be redefined by continuity, resulting in a continuous function at that point. These are, therefore, trivial singularities, which we will simply rule out of our discussions in this paper.

The concept of a singularity is the same, namely a point where the function is not analytic. The concepts of soft and hard singularities are carried in a straightforward way from the case of complex functions to that of real functions. The only significant difference is that the concept of the limit of the function to a point is now taken to be the real one, along the unit circle. The existence of the limit is a weaker condition in the real case, because in the complex case the limit must exist on and be independent of the continuum of directions along which one can take it along the complex plane, while in the real case the limit only has to exist and be the same along the two lateral directions. This means that, if one takes a path across a singularity of an analytic function in order to define a real function, the singularity of the real function may be soft even if the singularity of the analytic function is hard, and the singularity of the real function may be integrable even if the singularity of the analytic function is not.

At this point it is interesting to note that it might be useful to consider classifying all inner analytic functions $w(z)=u(\rho,\theta)+\mbox{\boldmath$\imath$} v(\rho,\theta)$ according to whether or not they have the same basic analytic properties, taken in the complex sense, as the corresponding real functions $u(1,\theta)$, taken in the real sense. One could say that a regular inner analytic function is one that has, at all its singular points on the unit circle, the same status as the corresponding real function, regarding the most fundamental analytic properties. By contrast, an irregular inner analytic function would be one that fails to have the same status as the corresponding real function, regarding one or more of the these analytic properties, such as those of integrability, continuity, and a given level of multiple differentiability.

The gradations corresponding to soft and hard singularities can be implemented for real functions in terms of the integrability or non-integrability of the singularities. The soft singularities are all integrable, and a singularity which is both hard and integrable is necessarily a borderline hard singularity, that can be immediately associated to the degree of hardness zero. The degree of softness of an isolated soft singularity is the number of differentiations with respect to $\theta$ of the real function $f(\theta)$, in a neighborhood of the singular point, which are required for the singularity to become a borderline hard one. Observing that a soft singularity of degree one means that the function is continuous but not differentiable, an alternative definition is that the degree of softness is one plus the number of differentiations with respect to $\theta$ of the real function $f(\theta)$, in a neighborhood of the singular point, which are required for the function to become non-differentiable at that point. The remaining problem is that of associating a degree of hardness to non-integrable hard singularities. This is the most important part of this structure in regard to our work in this paper, so let us examine it in more detail.

Let us assume that the real function $f(\theta)$ has an isolated non-integrable singular point at $\theta_{1}$, which is therefore a hard singularity. What we mean here by this singularity being isolated is that the function has no other non-integrable hard singularities in a neighborhood of that point, and is thus integrable in each one of the two sides of that neighborhood. Consider then two points within that neighborhood on the unit circle, say $\theta_{\ominus}$ and $\theta_{\oplus}$, one to the left and the other to the right of $\theta_{1}$, so that we have $\theta_{\ominus}<\theta_{1}<\theta_{\oplus}$. It follows, therefore, that the function $f(\theta)$ is an integrable real function on the two closed intervals $[\theta_{\ominus},\theta_{1}-\varepsilon_{\ominus}]$ and $[\theta_{1}+\varepsilon_{\oplus},\theta_{\oplus}]$, where $\varepsilon_{\ominus}$ and $\varepsilon_{\oplus}$ are any sufficiently small strictly positive real numbers, such that $\theta_{\ominus}<\theta_{1}-\varepsilon_{\ominus}$ and $\theta_{1}+\varepsilon_{\oplus}<\theta_{\oplus}$. Therefore, we can integrate the function $f(\theta)$ within these two intervals, starting at some arbitrary reference points $\theta_{0,\ominus}$ and $\theta_{0,\oplus}$ strictly within each interval, defining in this way a pair of sectional primitives $f_{\ominus}^{-1\prime}(\theta)$ and $f_{\oplus}^{-1\prime}(\theta)$, one within each interval,

$$f_{\ominus}^{-1\prime}(\theta) = \int_{\theta_{0,\ominus}}^{\theta}d\theta'\, f(\theta'),$$

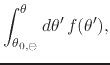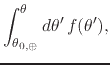$$f_{\oplus}^{-1\prime}(\theta) = \int_{\theta_{0,\oplus}}^{\theta}d\theta'\, f(\theta'),$$ (4)

where we have that both the argument $\theta$ and the reference points $\theta_{0,\ominus}$ and $\theta_{0,\oplus}$ are within the corresponding closed integration intervals. Therefore, on the left interval we have that $\theta_{\ominus}\leq\theta\leq\theta_{1}-\varepsilon_{\ominus}$ and that $\theta_{\ominus}\leq\theta_{0,\ominus}\leq\theta_{1}-\varepsilon_{\ominus}$, while on the right interval we have that $\theta_{1}+\varepsilon_{\oplus}\leq\theta\leq\theta_{\oplus}$ and that $\theta_{1}+\varepsilon_{\oplus}\leq\theta_{0,\oplus}\leq\theta_{\oplus}$. Note that, since $f(\theta)$ is integrable on those closed intervals, it follows that the piecewise primitive $f^{-1\prime}(\theta)$ formed by the pair of sectional primitives $f_{\ominus}^{-1\prime}(\theta)$ and $f_{\oplus}^{-1\prime}(\theta)$ is limited on those same closed intervals, and therefore is also integrable on them. Therefore, this process of sectional integration of the functions can be iterated indefinitely. Let us assume that we iterate this process $n$ times, thus obtaining the $n$-fold primitive $f^{-n\prime}(\theta)$.

In general one cannot take the limits $\varepsilon_{\ominus}\to 0$ or $\varepsilon_{\oplus}\to 0$, because the singularity at $\theta_{1}$ is a non-integrable one and therefore the limits of the asymptotic integrals on either side will diverge. However, if there is a number $n$ of successive sectional integrations such that the resulting primitive $f^{-n\prime}(\theta)$ has a borderline hard singularity at $\theta_{1}$, being therefore integrable on the whole closed interval $[\theta_{\ominus},\theta_{\oplus}]$, then the two limits $\varepsilon_{\ominus}\to 0$ and $\varepsilon_{\oplus}\to 0$ can both be taken. In this case we may say that the hard singularity of $f(\theta)$ at $\theta_{1}$ has degree of hardness $n$. In Section 4 we will have the opportunity to use these ideas regarding sectional integration on closed intervals that avoid non-integrable singular points.