Next: Conclusions and Outlook Up: Complex Analysis of Real Previous: Representation of Non-Integrable Real
Assuming that, given a non-integrable real function ![]() , the
corresponding reduced inner analytic function
, the
corresponding reduced inner analytic function
![]() has been determined,
we may now consider determining a unique set of Fourier coefficients to be
associated to the non-integrable real function
has been determined,
we may now consider determining a unique set of Fourier coefficients to be
associated to the non-integrable real function ![]() . Of these,
. Of these,
![]() has already been determined, through the comparison of
has already been determined, through the comparison of
![]() and
and ![]() at some point of the unit circle where
they do not have hard singularities. It follows that
at some point of the unit circle where
they do not have hard singularities. It follows that
![]() has also been determined. From the Taylor series of
has also been determined. From the Taylor series of ![]() ,
,
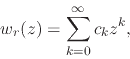 |
(38) |
we have the values of all the other Taylor coefficients ![]() , for
, for
![]() . Given that in this case we have that
. Given that in this case we have that
![]() , we immediately get the values of all the
other Fourier coefficients
, we immediately get the values of all the
other Fourier coefficients ![]() and
and ![]() . Note that this
construction has the effect of associating a complete set of Fourier
coefficients
. Note that this
construction has the effect of associating a complete set of Fourier
coefficients ![]() ,
, ![]() and
and ![]() , for
, for
![]() , to the non-integrable real function
, to the non-integrable real function
![]() . In particular, the association of
. In particular, the association of ![]() has the effect
of attributing an average value to the non-integrable real function
has the effect
of attributing an average value to the non-integrable real function
![]() , which has been defined via an analytic process.
, which has been defined via an analytic process.
Although these coefficients obviously cannot be written in terms of
integrals involving ![]() in the usual way, all of them except for
in the usual way, all of them except for
![]() can, in fact, be written as a certain set of integrals. In
order to do this, we start by considering the
can, in fact, be written as a certain set of integrals. In
order to do this, we start by considering the ![]() angular
primitive
angular
primitive
![]() of the reduced inner analytic function
of the reduced inner analytic function
![]() , which is, therefore, a proper inner analytic function, and the
known associated Fourier and Taylor coefficients, which we will name
, which is, therefore, a proper inner analytic function, and the
known associated Fourier and Taylor coefficients, which we will name
![]() ,
,
![]() and
and
![]() , for
, for
![]() , and
, and ![]() , for
, for
![]() . Since it has at most borderline hard
singularities on the unit circle, this inner analytic function corresponds
to an integrable real function
. Since it has at most borderline hard
singularities on the unit circle, this inner analytic function corresponds
to an integrable real function
![]() on that circle,
on that circle,
| (39) |
so that the Fourier coefficients of
![]() can be
written as integrals involving this function,
can be
written as integrals involving this function,
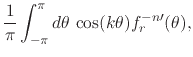 |
|||
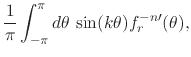 |
(40) |
for
![]() . We now recall that we have for the
Taylor series of the
. We now recall that we have for the
Taylor series of the ![]() angular primitive of
angular primitive of ![]() ,
,
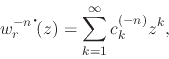 |
(41) |
and therefore the ![]() angular derivative of this equation is
given by
angular derivative of this equation is
given by
![\begin{displaymath}
w_{r}^{0\mbox{\Large$\cdot$}\!}(z)
=
\sum_{k=1}^{\infty}
...
...
\mbox{\boldmath$\imath$}^{n}k^{n}c_{k}^{(-n)}
\right]z^{k},
\end{displaymath}](img206.png) |
(42) |
where
![]() is the proper inner analytic function associated
to
is the proper inner analytic function associated
to ![]() . It thus follows that we have for the Taylor coefficients
. It thus follows that we have for the Taylor coefficients
![]() of
of
![]() , which are also the Taylor coefficients of
, which are also the Taylor coefficients of
![]() , for
, for
![]() ,
,
Since we know that the coefficients ![]() , being the Taylor
coefficients associated to an integrable real function, are limited for
all
, being the Taylor
coefficients associated to an integrable real function, are limited for
all ![]() , we may now conclude that the coefficients
, we may now conclude that the coefficients ![]() of the
non-integrable real function may diverge with
of the
non-integrable real function may diverge with ![]() , but not faster than the
power
, but not faster than the
power ![]() . We may write this relation in terms of the Fourier
coefficients
. We may write this relation in terms of the Fourier
coefficients ![]() and
and ![]() associated to the non-integrable
real function
associated to the non-integrable
real function ![]() , for
, for
![]() , if we recall
from [#!CAoRFI!#] that
, if we recall
from [#!CAoRFI!#] that
![]() , and also that
, and also that
![]() ,
,
![$\displaystyle \mbox{\boldmath$\imath$}^{n}k^{n}
\left[
\alpha_{k}^{(-n)}-\mbox{\boldmath$\imath$}\beta_{k}^{(-n)}
\right]$](img211.png) |
|||
| (44) |
We now see that the relations between the Fourier coefficients
![]() and the Fourier coefficients
and the Fourier coefficients
![$\left[\alpha_{k}^{(-n)},\beta_{k}^{(-n)}\right]$](img214.png) depend on the parity of
depend on the parity of
![]() . For even
. For even ![]() we have
we have
| (45) |
while for odd ![]() we have
we have
| (46) |
Since we have the coefficients
![]() and
and
![]() written as integrals, we may now write
written as integrals, we may now write ![]() and
and ![]() as
integrals, first for the case of even
as
integrals, first for the case of even ![]() ,
,
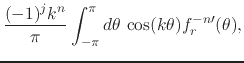 |
|||
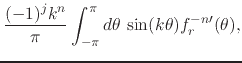 |
(47) |
and then for the case of odd ![]() ,
,
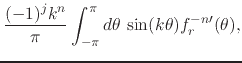 |
|||
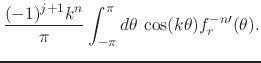 |
(48) |
Since the integrals shown are all limited as functions of ![]() , given that
, given that
![]() is an integrable real function, once again it
is apparent that the coefficients
is an integrable real function, once again it
is apparent that the coefficients ![]() and
and ![]() which are
associated to
which are
associated to ![]() typically diverge as a positive power of
typically diverge as a positive power of ![]() when
when ![]() . Note that, when the real function
. Note that, when the real function ![]() is
integrable on the whole unit circle, we are reduced to the case
is
integrable on the whole unit circle, we are reduced to the case ![]() , so
that the expressions for the even case reduce to the usual ones for the
Fourier coefficients.
, so
that the expressions for the even case reduce to the usual ones for the
Fourier coefficients.
In a previous paper [#!CAoRFIII!#] we showed that the whole Fourier
theory of integrable real functions is contained in the complex-analytic
structure introduced in [#!CAoRFI!#]. We also extended that Fourier
theory to include, not only the singular distributions discussed
in [#!CAoRFII!#], but essentially the whole space of inner analytic
functions. We now observe that the sequences of complex Taylor
coefficients ![]() in Equation (43), which go to infinity
with
in Equation (43), which go to infinity
with ![]() not faster than a power, are exponentially bounded, according to
the definition of that term given in [#!CAoRFIII!#], and repeated in
Equation (7). This in itself suffices to show that the
corresponding power series converges to an inner analytic function, as was
shown in that paper. It also implies, as was also shown there, that the
two sequences of real coefficients
not faster than a power, are exponentially bounded, according to
the definition of that term given in [#!CAoRFIII!#], and repeated in
Equation (7). This in itself suffices to show that the
corresponding power series converges to an inner analytic function, as was
shown in that paper. It also implies, as was also shown there, that the
two sequences of real coefficients ![]() and
and ![]() associated
to
associated
to ![]() are both also exponentially bounded. As a consequence of
all this, the non-integrable real functions we are discussing in this
paper can be expressed as regulated Fourier series, as given in
Equation (8), thus using the summation rule that was
presented in [#!CAoRFIII!#],
are both also exponentially bounded. As a consequence of
all this, the non-integrable real functions we are discussing in this
paper can be expressed as regulated Fourier series, as given in
Equation (8), thus using the summation rule that was
presented in [#!CAoRFIII!#],
![\begin{displaymath}
f(\theta)
=
\frac{\alpha_{0}}{2}
+
\lim_{\rho\to 1_{(-)...
...
\alpha_{k}\cos(k\theta)
+
\beta_{k}\sin(k\theta)
\right],
\end{displaymath}](img227.png) |
(49) |
which is equivalent to the fact that the non-integrable real functions
which we discussed here can be obtained as the
![]() limits of
the real parts of inner analytic functions. We see therefore that the
class of non-integrable real functions which we are examining here is also
contained in the extended Fourier theory presented in [#!CAoRFIII!#].
limits of
the real parts of inner analytic functions. We see therefore that the
class of non-integrable real functions which we are examining here is also
contained in the extended Fourier theory presented in [#!CAoRFIII!#].