Fixed Boundary Conditions

**Figure 5:** The same fixed-boundary lattice, showing a possible cluster that might have been built in it, with part of it connected to the boundary.
$\begin{figure}\centering \epsfig{file=cluster-fixed.fps,scale=0.7,angle=0} \end{figure}$

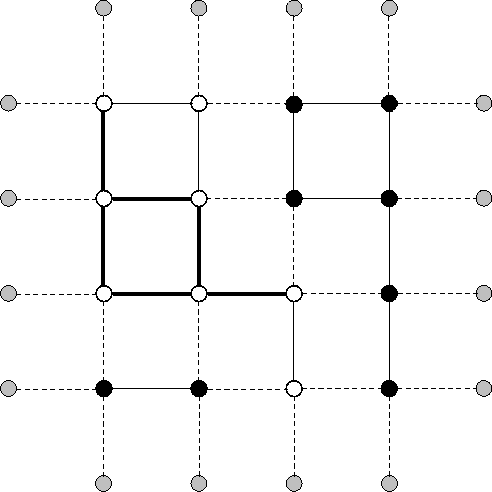
Let us now discuss what happens when we use a lattice with fixed instead of periodical boundary conditions. In this case the lattice has a boundary, where the field is kept at fixed values, which are not necessarily constant over the boundary, and which, even in the Ising model, are not necessarily just $\pm 1$ . In figure 4 one can see an example of such a lattice, with all its sites and links dully classified. The sites at the external boundary are shown in gray. Note that all the links to the sites at the boundary are represented by dashed lines, because one cannot ever activate these links, since that would force us to flip the fields at the boundary, and of course changing the fields at the boundary is not allowed under these circumstances.

One can see without difficulty that one can use the algorithm to build clusters in the usual way in the interior, once the links to the external boundary are marked as non-candidates for activation. Once the cluster is built, there are two possibilities: if the cluster includes no sites that are connected to the boundary sites, then one can go ahead and flip it as usual; if the cluster does include one or more sites connected to the external boundary, then flipping it will change a part of the action which is being ignored by the building algorithm, namely the terms relating to links connecting to the boundary sites. In this last case the situation is similar to the situation discussed in the previous section for the case of external sources, namely there is a part of the action that has to be taken into account separately.

In figure 5 one can see an example of a cluster built on the lattice, including a few sites that are connected to the boundary. The same type of solution used in the previous section applies in this case as well, but in this case the relevant separation of the action is two parts is

$\begin{displaymath} S[\psi]=S_{i}[\psi]+S_{b}[\psi] =-\beta\sum_{\ell_{i}}\psi_{-}\psi_{+}-\beta\sum_{\ell_{b}}\psi_{-}\psi_{+} \end{displaymath}$

where $\ell_{i}$ are the links strictly in the interior of the lattice and $\ell_{b}$ are those connecting the interior to the boundary. The interior part $S_{i}$ of the action is taken into consideration by the cluster-building algorithm, and the boundary part $S_{b}$ can be taken into account by a Metropolis test done afterwards, giving the probability that the cluster will be flipped. Here is the algorithm for this case:

Choose a single site of the interior the of lattice for starting to build the cluster, in a random way.
Consider all the links connected to that initial site, which are not connected to the external boundary; the $\ell_{-}$ links are never to be activated; activate the $\ell_{+}$ links with the probability $p_{+}=1-\exp(-2\beta\psi_{-}\psi_{+})$ , thus forming a first cluster of sites, that is, updating the cluster from a single site to possibly a few sites.
Given the set of sites added to the cluster in the previous update of the cluster (which is not the whole cluster), consider all the links that connect those sites to sites that are still outside the cluster, and which are not in the external boundary; among these, activate the $\ell_{+}$ links with the probability $p_{+}$ , thus enlarging (updating) the cluster.
Loop back to step until the set of links left for activation trial in the next round of the loop is empty; this means that you stop this loop at the first instance of step that adds no new sites to the cluster.
Calculate the variation $\Delta S_{b}$ of the boundary term of the action caused by flipping the cluster just built; this will of course be zero if there are no sites in the cluster connected to sites in the boundary.
If it happens that $\Delta S_{b}\leq 0$ , then flip the cluster with probability equal to .
If $\Delta S_{b}>0$ , then flip the cluster with probability $\exp(-\Delta S_{b})$ ; if the update is rejected, repeat the current configuration in the stochastic sequence.
Loop back to step , in order to build and possibly flip a new cluster.

One can see that, just as in the case of external sources, in this case also the algorithm is inevitably somewhat less efficient than the pure Wolff algorithm, in terms of diffusion speed through configuration space. This will happen mostly in the rather unlikely case when one has very large values at the boundary, and also for very small lattices, since the ratio of the number of boundary sites to the number of internal sites is much larger on small lattices, specially in the larger dimensions. Just as in the case of external sources, in this case also we have no control over the rejection rate, although this tends to be a lesser problem here than in the case of the presence of a bulk term in the action, as is the case of the external-sources term. Of course, one can easily combine fixed boundary conditions with the presence of external sources, by simply considering for the Metropolis test all parts of the action which are not taken into consideration by the cluster-building algorithm.