Next: Arbitrary External Sources Up: The Wolff Algorithm with Previous: The Wolff Algorithm with
The traditional Metropolis algorithm, when applied do the Ising models close to their critical points, suffers from severe critical slowing down problems. This is due to its single-site updating procedure, which is good for updating the short-wavelength components of the configurations, but very bad at updating the long-wavelength components. Near the critical point the long-wavelength components play an important role due to the emergence of long-distance correlations, and in these circumstances the algorithm tends to diffuse only very slowly through the configuration space of the model. This increases the autocorrelations along the stochastic sequence of configurations and severely degrades the statistical quality of the results.
This is always a problem is the case of quantum field theory, since in that theory we are interested primarily in the critical region of the statistical models. If we are to use the Ising model in the analysis of problems in quantum field theory, we must use simulation techniques that do not suffer from such problems. The cluster algorithms are the answer to our needs, and among them the Wolff algorithm is particularly well suited for the task, due to its simplicity and efficiency. Cluster algorithms are characterized by the updating of whole sets of sites, or clusters, at a time, and in doing this they solve the problem of critical slowing down. The problem of how to make collective updates with a low rate of rejection and in such a way that the required statistical distribution is still produced correctly is a very difficult one, which was solved by the inventors of the cluster algorithms.
In this section we will describe the basic algorithm and show that it satisfied the condition of detailed balance, thus converging to the correct distribution. After that we will generalize the algorithm to the case in which we introduce external sources in the systems, as well as to the case in which we use fixed rather than the more usual periodical boundary conditions. This last topic will also lead us to consider the use of truncated clusters, a variation of the algorithm which may be useful under some circumstances.
Let us start by reviewing the fundamentals of the Metropolis algorithm.
In order to do that we must first establish some notation. Consider a
model in quantum field theory defined by an action functional ![]() ,
where
,
where ![]() is the field. This action determines the distribution of
probabilities for all the possible configurations
is the field. This action determines the distribution of
probabilities for all the possible configurations ![]() of the field, which
is given by
of the field, which
is given by
![]() , where
, where ![]() is a normalization
constant and the dependence on the field can be represented either by
is a normalization
constant and the dependence on the field can be represented either by
![]() or by
or by ![]() . What a simulation algorithm does is to establish
a probability
. What a simulation algorithm does is to establish
a probability
![]() for going from a configuration
for going from a configuration ![]() to
a configuration
to
a configuration ![]() on a single iteration of the algorithm. By iterating
the algorithm indefinitely one produces a sequence of configurations with
a distribution of probabilities that is supposed to approach
on a single iteration of the algorithm. By iterating
the algorithm indefinitely one produces a sequence of configurations with
a distribution of probabilities that is supposed to approach ![]() .
.
In order for this to work, it suffices that the algorithm satisfy two
conditions: ergodicity and detailed balance. Although not strictly
necessary, these conditions are sufficient to ensure convergence to the
correct distribution. Ergodicity means that any configuration ![]() should
be reachable from any other configuration
should
be reachable from any other configuration ![]() in a finite number of
iterations of the algorithm. In other words, the algorithm should never
get stuck in any particular configuration that it is unable to leave, and
there should be no configuration that it cannot reach from some other
configuration. This means that the algorithm should be able to diffuse
through the whole space of possible configurations of the field, without
leaving out any points or regions within it. Note that no statement is
made here about how fast it is able to diffuse. Of course, in practice
the quality of the algorithm will depend on it being able to do so fast,
because the space of configurations is usually very large.
in a finite number of
iterations of the algorithm. In other words, the algorithm should never
get stuck in any particular configuration that it is unable to leave, and
there should be no configuration that it cannot reach from some other
configuration. This means that the algorithm should be able to diffuse
through the whole space of possible configurations of the field, without
leaving out any points or regions within it. Note that no statement is
made here about how fast it is able to diffuse. Of course, in practice
the quality of the algorithm will depend on it being able to do so fast,
because the space of configurations is usually very large.
The condition of detailed balance is the one which will mostly concern us
here. It is a relation between the probability
![]() of
going from the configuration
of
going from the configuration ![]() to the configuration
to the configuration ![]() and the
probability
and the
probability
![]() of doing the reversed update, that is,
of going from
of doing the reversed update, that is,
of going from ![]() to
to ![]() , and involves the probabilities
, and involves the probabilities ![]() and
and
![]() of the two configurations involved, within the ensemble of all
possible configurations. It states that the ratio of these two
probabilities should satisfy the condition
of the two configurations involved, within the ensemble of all
possible configurations. It states that the ratio of these two
probabilities should satisfy the condition
![\begin{displaymath}
\frac{W[C\rightarrow C']}{W[C'\rightarrow C]}=\frac{P[C']}{P[C]}.
\end{displaymath}](img13.gif)
Since the probabilities of the configurations can be written in terms of the action, this condition can be translated into
![\begin{displaymath}
\frac{W[C\rightarrow C']}{W[C'\rightarrow C]}
=\frac{\exp(-S[C'])}{\exp(-S[C])}=\exp(-S[C']+S[C])=\exp(-\Delta S),
\end{displaymath}](img14.gif)
where ![]() is the change in the action due to the update of the
configuration. It is possible to show by elementary means, in a simple
one-dimensional case, that this condition is sufficient to guarantee that
the set of configurations produced by the algorithm converges to the
correct distribution. However, that is not our focus here, and we will
simply take it as a given fact. Let us now describe in detail the usual
Metropolis algorithm for a single local update in the Ising model, and
show that it satisfies this condition. Starting from some initial
configuration, the Metropolis single-site updating algorithm is given by
the following sequence of steps:
is the change in the action due to the update of the
configuration. It is possible to show by elementary means, in a simple
one-dimensional case, that this condition is sufficient to guarantee that
the set of configurations produced by the algorithm converges to the
correct distribution. However, that is not our focus here, and we will
simply take it as a given fact. Let us now describe in detail the usual
Metropolis algorithm for a single local update in the Ising model, and
show that it satisfies this condition. Starting from some initial
configuration, the Metropolis single-site updating algorithm is given by
the following sequence of steps:
As one can see, the algorithm is very simple and easily generalizable to
more complex models. It is also possible to improve it in various rather
technical ways, that help in some cases but that do not solve the central
problem of critical slowing down caused by the local update. It is now
easy to verify that this algorithm satisfies the condition of detailed
balance. We must consider three cases, depending on whether the variation
of the action is positive, zero or negative. If the update is such that
![]() , then we have for its probability
, then we have for its probability
![]() ; in this case the reversed update is such that
; in this case the reversed update is such that
![]() , so that we have for its probability
, so that we have for its probability
![]() ;
it therefore follows that
;
it therefore follows that
![\begin{displaymath}
\frac{W[C\rightarrow C']}{W[C'\rightarrow C]} =\frac{\exp(-\Delta
S)}{1}=\exp(-\Delta S),
\end{displaymath}](img24.gif)
as required by the condition. If the update is such that ![]() ,
then the probability for the update is
,
then the probability for the update is
![]() , and the
probability for the reversed update is
, and the
probability for the reversed update is
![]() , where
, where
![]() is the variation of the
action in the reversed update; it therefore follows that
is the variation of the
action in the reversed update; it therefore follows that
![\begin{displaymath}
\frac{W[C\rightarrow C']}{W[C'\rightarrow C]} =\frac{1}{\exp(\Delta
S)}=\exp(-\Delta S),
\end{displaymath}](img28.gif)
 |
just as in the previous case. If ![]() , then we also have
, then we also have
![]() , and hence
, and hence
![]() , so
that the ratio of the two updating probabilities is equal to
, so
that the ratio of the two updating probabilities is equal to ![]() ; since
in this case
; since
in this case
![]() is also equal to
is also equal to ![]() , we see that
in all three cases the condition is satisfied.
, we see that
in all three cases the condition is satisfied.
In order to discuss the Wolff algorithm, we must now establish a few more concepts and notations. The basic idea of the algorithm will be to first built a cluster of sites according to certain rules, and then to flip the whole cluster. The cluster will be built by the ``activation'' of some of the links between two neighboring sites, and requires that we classify the links according to whether it connects two sites where the field has the same orientation, or opposite orientations. At first, let us consider only lattices with periodical boundary conditions and the model in the absence of any external sources. Later on we will extend the algorithm to these other cases. We should recall here that the Ising model is defined by the action
![\begin{displaymath}
S[\psi]=-\beta\sum_{\ell}\psi_{-}\psi_{+},
\end{displaymath}](img34.gif)
where
![]() is the free parameter of the model, the sum is
over the links and
is the free parameter of the model, the sum is
over the links and ![]() ,
, ![]() are the values of the field at
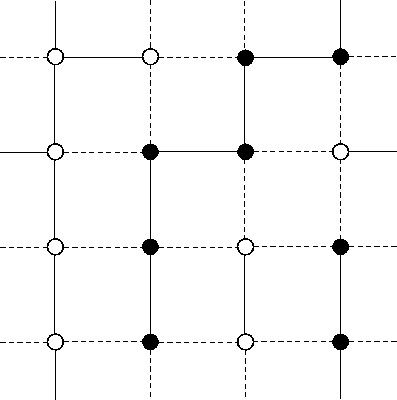
the two ends of a given link. In figure 1 one can
see an example of a two-dimensional periodical lattice with all its sites
and links dully classified. The sites where the field is positive are
shown as black circles and those where the field is negative as white
circles. The links that connect two sites with the same orientation are
shown as solid lines, and those connecting sites with opposite
orientations as dashed lines. Note that this is true for the border links
as well, which establish the periodical boundary conditions. The links
represented by solid lines will be denoted by
are the values of the field at
the two ends of a given link. In figure 1 one can
see an example of a two-dimensional periodical lattice with all its sites
and links dully classified. The sites where the field is positive are
shown as black circles and those where the field is negative as white
circles. The links that connect two sites with the same orientation are
shown as solid lines, and those connecting sites with opposite
orientations as dashed lines. Note that this is true for the border links
as well, which establish the periodical boundary conditions. The links
represented by solid lines will be denoted by ![]() in the formulas,
and those represented by dashed lines by
in the formulas,
and those represented by dashed lines by ![]() . According to the
algorithm only
. According to the
algorithm only ![]() links can be activated to form clusters, so the
sets of sites connected by solid lines illustrate the clusters that can
be formed in this particular configuration. We may now state the Wolff
algorithm, which is given by the following sequence of steps:
links can be activated to form clusters, so the
sets of sites connected by solid lines illustrate the clusters that can
be formed in this particular configuration. We may now state the Wolff
algorithm, which is given by the following sequence of steps:
Note that in steps ![]() and
and ![]() , since only
, since only ![]() links can be
activated, the argument of the exponential is negative and thus
links can be
activated, the argument of the exponential is negative and thus
![]() is a number in the interval
is a number in the interval ![]() .
Therefore, so is the probability
.
Therefore, so is the probability
![]() .
Note also that during the construction of the cluster a certain site may
be approached by the growing cluster from two or more different
directions, along different links. If that site does not get linked to
the cluster at the first trial, it might still get linked at a later
trial. The algorithm implies that the same link is never tried more than
once for activation, but a single site my be tried more than once for
linking to the cluster, if it has more than one link able to be
activated. Finally, observe that during construction it might happen that
two sites already included in the cluster are connected by a link that
has not yet been tried. That link will in fact never be tried by the
algorithm, and may be considered as automatically activated, that is,
they can simply be activated with probability
.
Note also that during the construction of the cluster a certain site may
be approached by the growing cluster from two or more different
directions, along different links. If that site does not get linked to
the cluster at the first trial, it might still get linked at a later
trial. The algorithm implies that the same link is never tried more than
once for activation, but a single site my be tried more than once for
linking to the cluster, if it has more than one link able to be
activated. Finally, observe that during construction it might happen that
two sites already included in the cluster are connected by a link that
has not yet been tried. That link will in fact never be tried by the
algorithm, and may be considered as automatically activated, that is,
they can simply be activated with probability ![]() at the end of the
construction. A simple cluster that could result from the algorithm is
shown in figure 2, with its sites and activated
links, which are shown in a thicker solid line.
at the end of the
construction. A simple cluster that could result from the algorithm is
shown in figure 2, with its sites and activated
links, which are shown in a thicker solid line.
Let us now show that this algorithm satisfied the condition of detailed
balance. In order to do this, given a certain cluster, we must calculate
the probability that it will be built and flipped. We will denote the
cluster by ![]() and the boundary of the cluster, that is, the set of
links that connect the cluster with sites outside the cluster, by
and the boundary of the cluster, that is, the set of
links that connect the cluster with sites outside the cluster, by
![]() .
In figure 3 one can see a larger lattice with a cluster
that could have been built by the algorithm, as well as its boundary,
illustrated by the thick dotted line which crosses all the links that
connect the cluster to sites outside the cluster. Since the probability
of flipping a cluster is
.
In figure 3 one can see a larger lattice with a cluster
that could have been built by the algorithm, as well as its boundary,
illustrated by the thick dotted line which crosses all the links that
connect the cluster to sites outside the cluster. Since the probability
of flipping a cluster is ![]() , once it has been built, we must simply
calculate the total probability of building a certain given cluster. The
process of building the cluster might start at any of its sites, so we
start the calculation with the probability that one of the sites of the
cluster will be chosen in step
, once it has been built, we must simply
calculate the total probability of building a certain given cluster. The
process of building the cluster might start at any of its sites, so we
start the calculation with the probability that one of the sites of the
cluster will be chosen in step ![]() of the algorithm. Let us call this
probability
of the algorithm. Let us call this
probability ![]() , and there is no need to further elaborate on it.
, and there is no need to further elaborate on it.
Irrespective of where the construction starts, the probability that the
given cluster will be built is the product of the probabilities that each
one of its internal links will be activated, times the product of the
probabilities that each one of the links of its borders will not be
activated. Now, all the internal links are ![]() links, so the
probability that they will be activated is given by
links, so the
probability that they will be activated is given by
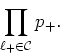
For the ![]() links in the border of the cluster not to be
activated we have the probability
links in the border of the cluster not to be
activated we have the probability
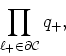
where
![]() is the complementary
probability to
is the complementary
probability to ![]() . Since the probability for the
. Since the probability for the ![]() links at
the border not to be activated is
links at
the border not to be activated is ![]() , this product is the complete
probability for the construction of the boundary. We have therefore the
complete probability for the construction of the cluster, and hence the
complete probability for the update of the configuration,
, this product is the complete
probability for the construction of the boundary. We have therefore the
complete probability for the construction of the cluster, and hence the
complete probability for the update of the configuration,
![\begin{displaymath}
W[C\rightarrow C']=p_{i}\left(\prod_{\ell_{+}\in{\cal C}}p_{+}\right)
\left(\prod_{\ell_{+}\in{\partial\cal C}}q_{+}\right).
\end{displaymath}](img53.gif)
Next we must consider the probability for the reversed update. Since the
same set of sites that makes up the cluster ![]() in the configuration
in the configuration ![]() also makes up the flipped cluster
also makes up the flipped cluster ![]() in the configuration
in the configuration ![]() , it is
clear that the probability
, it is
clear that the probability ![]() is the same in either case. Now,
repeating the argument used for the cluster
is the same in either case. Now,
repeating the argument used for the cluster ![]() we get for the
probability that the cluster
we get for the
probability that the cluster ![]() will be built
will be built
![\begin{displaymath}
W[C'\rightarrow C]=p_{i}\left(\prod_{\ell_{+}\in{\cal C}'}p_...
...right)
\left(\prod_{\ell_{+}\in{\partial\cal C}'}q_{+}\right).
\end{displaymath}](img55.gif)
Observe now that when we flip the fields certain mappings between links
take place. When we go from the cluster ![]() to the flipped cluster
to the flipped cluster
![]() , we can see that all the internal
, we can see that all the internal ![]() links of
links of ![]() become
internal
become
internal ![]() links of
links of ![]() , since the fields at both ends of each
link get flipped and hence their product does not change sign. This means
that the first products that appears in the two formulas above are equal,
and therefore that we may write the ratio of the two probabilities as
, since the fields at both ends of each
link get flipped and hence their product does not change sign. This means
that the first products that appears in the two formulas above are equal,
and therefore that we may write the ratio of the two probabilities as
![\begin{displaymath}
\frac{W[C\rightarrow C']}{W[C'\rightarrow C]}
=\frac{\prod_{...
...tial\cal C}}q_{+}}{\prod_{\ell_{+}\in{\partial\cal C}'}q_{+}}.
\end{displaymath}](img56.gif)
For the links at the border, however, we have that the ![]() links
of
links
of
![]() become the
become the ![]() links of
links of
![]() , and that the
, and that the ![]() links of
links of
![]() become the
become the ![]() links of
links of
![]() , since for these
links only the field at one end gets flipped and therefore the sign of
the product changes. In addition to this, the term of the action
corresponding to each link changes sign, so that the factor
, since for these
links only the field at one end gets flipped and therefore the sign of
the product changes. In addition to this, the term of the action
corresponding to each link changes sign, so that the factor ![]() gets
mapped to
gets
mapped to ![]() . If we write the ratio above in terms of the action
terms,
. If we write the ratio above in terms of the action
terms,
![\begin{displaymath}
\frac{W[C\rightarrow C']}{W[C'\rightarrow C]}
=\frac{\prod_{...
..._{\ell_{+}\in{\partial\cal C}'}\exp(-2\beta\psi_{-}\psi_{+})},
\end{displaymath}](img60.gif)
we see that we can decompose each one of the two products in two parts,
![\begin{displaymath}
\frac{W[C\rightarrow C']}{W[C'\rightarrow C]}=
\frac{\prod_{...
...d_{\ell_{+}\in{\partial\cal C}'}\exp(-\beta\psi_{-}\psi_{+})}.
\end{displaymath}](img61.gif)
Now, due to the mappings of the boundary links which we just discussed, we have that the following two equations hold,
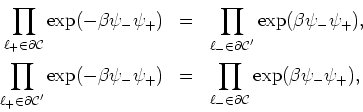
so that the ratio of updating probabilities may be written as
![\begin{eqnarray*}
\frac{W[C\rightarrow C']}{W[C'\rightarrow C]} & = &
\frac{\pro...
...\prod_{\ell_{-}\in{\partial\cal C}}\exp(\beta\psi_{-}\psi_{+})}.
\end{eqnarray*}](img63.gif)
Note that in this way we have completed the set of boundary links in both the numerator and the denominator, so that we may write
![\begin{displaymath}
\frac{W[C\rightarrow C']}{W[C'\rightarrow C]}
=\frac{\prod_{...
...}
{\exp(\sum_{\ell\in{\partial\cal C}}\beta\psi_{-}\psi_{+})}.
\end{displaymath}](img64.gif)
What we see here in the argument of the two exponentials in the last form
of this equation is the negative of the part of the action that
corresponds to the boundary links, which we may denote by
![]() . We may therefore write
the ratio of the two updating probabilities as
. We may therefore write
the ratio of the two updating probabilities as
![\begin{displaymath}
\frac{W[C\rightarrow C']}{W[C'\rightarrow C]}
=\frac{\exp(-S_{B}[C'])}{\exp(-S_{B}[C'])}=\exp(-\Delta S_{B}).
\end{displaymath}](img66.gif)
Since in the flipping of a cluster the parts of the action corresponding
to links that are either completely internal to the cluster or completely
external to it do not change at all, the only variation of the action is
that due to the boundary links, which means that
![]() ,
and hence we get the final relation
,
and hence we get the final relation
![\begin{displaymath}
\frac{W[C\rightarrow C']}{W[C'\rightarrow C]}=\exp(-\Delta S),
\end{displaymath}](img68.gif)
which is indeed the condition of detailed balance, as we set out to show. Please note how important it is for this demonstration the fact that the update of a cluster changes the action exclusively at the boundary links of the cluster, and not at its bulk, that is, at its interior sites and links.