Next: A Regular Sine Series Up: Appendix: Examples of Center Previous: Appendix: Examples of Center
Consider the Fourier series of the one-cycle unit-amplitude sawtooth wave,
which is just the linear function ![]() between
between ![]() and
and ![]() .
As is well known it is given by the sine series
.
As is well known it is given by the sine series
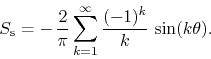
The corresponding FC series is then
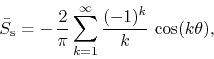
the complex ![]() series is given by
series is given by
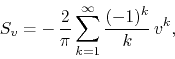
and the complex power series ![]() is given by
is given by
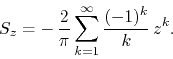
The ratio test tells us that the disk of convergence of ![]() is the
unit disk. If we consider the inner analytic function
is the
unit disk. If we consider the inner analytic function ![]() within this
disk we observe that
within this
disk we observe that ![]() , as expected. We have for this function
, as expected. We have for this function
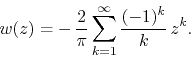
Being given by a monotonic series of step ![]() modified by the factor of
modified by the factor of
![]() , this function has a single dominant singularity at
, this function has a single dominant singularity at ![]() ,
where it diverges to infinity, as one can easily verify
,
where it diverges to infinity, as one can easily verify
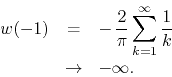
We must therefore use a single factor of ![]() in the construction of
the center series,
in the construction of
the center series,
![\begin{eqnarray*}
C_{z}
& = &
-\,
\frac{2}{\pi}\,
(z+1)
\sum_{k=1}^{\infty...
... \sum_{k=1}^{\infty}
\frac{(-1)^{k}}{k(k+1)}\,
z^{k}
\right].
\end{eqnarray*}](img244.png)
Unlike the original series, with coefficients that behave as ![]() , this
series has coefficients that go to zero as
, this
series has coefficients that go to zero as ![]() when
when ![]() ,
and therefore is absolutely and uniformly convergent to a continuous
function. This shows, in particular, that our evaluation of the set of
dominant singularities of
,
and therefore is absolutely and uniformly convergent to a continuous
function. This shows, in particular, that our evaluation of the set of
dominant singularities of ![]() was in fact correct. We have therefore
for
was in fact correct. We have therefore
for ![]() the representation
the representation
![\begin{displaymath}
S_{z}
=
\frac{2}{\pi}\,
\frac{z}{z+1}
\left[
1
-
\sum_{k=1}^{\infty}
\frac{(-1)^{k}}{k(k+1)}\,
z^{k}
\right],
\end{displaymath}](img245.png)
with the singularity factored out and where the series involved is absolutely and uniformly convergent, and therefore converges much faster than the original one.
We may now take the real and imaginary parts of the ![]() series in
order to obtain faster-converging representation of the original DP
Fourier series and its FC series. We have on the unit circle
series in
order to obtain faster-converging representation of the original DP
Fourier series and its FC series. We have on the unit circle
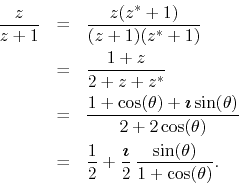
If we write this in terms of ![]() we get
we get
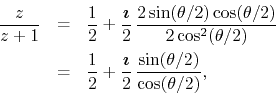
and therefore
![\begin{eqnarray*}
S_{v}
& = &
\frac{1}{\pi}
\left[
1
+
\mbox{\boldmath$\i...
...}{k(k+1)}\,
\sin\!\left(\frac{2k+1}{2}\,\theta\right)
\right].
\end{eqnarray*}](img249.png)
The original DP function is given by the imaginary part,
![\begin{displaymath}
f_{\rm s}(\theta)
=
\frac{1}{\pi\cos(\theta/2)}
\left[
...
...k(k+1)}\,
\sin\!\left(\frac{2k+1}{2}\,\theta\right)
\right],
\end{displaymath}](img250.png)
and the corresponding FC function
![]() is given by the real part,
is given by the real part,
![\begin{displaymath}
f_{\rm c}(\theta)
=
\frac{1}{\pi\cos(\theta/2)}
\left[
...
...k(k+1)}\,
\cos\!\left(\frac{2k+1}{2}\,\theta\right)
\right].
\end{displaymath}](img252.png)
Both of these series are absolutely and uniformly convergent.