Next: Appendix: Technical Proofs Up: Fourier Theory on the Previous: Acknowledgements
It is interesting to point out that a certain lacunary (or lacunar) trigonometric series proposed by Riemann, as a possible example of a continuous function that is not differentiable anywhere, can be analyzed in the context of the relationship presented in this paper. Riemann proposed the sine series
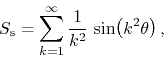
from which we can construct the FC cosine series
![]() ,
,
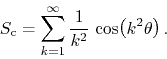
Both series pass the Weierstrass ![]() -test and are therefore uniformly
convergent to continuous functions over the whole periodic interval.
Their term-by-term derivatives, however, are not convergent at all,
-test and are therefore uniformly
convergent to continuous functions over the whole periodic interval.
Their term-by-term derivatives, however, are not convergent at all,
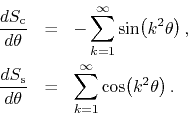
All these series can be understood as trigonometric series in which the
coefficients ![]() corresponding to values of
corresponding to values of ![]() which are not perfect
squares are all zero. Therefore, there are lots of missing terms, hence
the name ``lacunary'' series. Since the two trigonometric series
which are not perfect
squares are all zero. Therefore, there are lots of missing terms, hence
the name ``lacunary'' series. Since the two trigonometric series ![]() and
and ![]() are the FC series of each other, they can be used to
construct the complex power series
are the FC series of each other, they can be used to
construct the complex power series
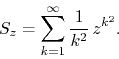
This is a lacunary power series which presumably has a countable infinity of soft singularities densely distributed over the unit circle. The ratio test tells us that the maximum disk of convergence of this series is indeed the open unit disk. We have therefore an inner analytic function defined on that disk,
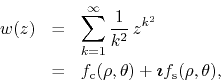
where
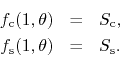
Since the trigonometric series are convergent on the whole unit circle,
due to Abel's theorem [6] the ![]() limits of this
function from within the unit disk exists everywhere on that circle. The
derivative
limits of this
function from within the unit disk exists everywhere on that circle. The
derivative ![]() of this function is also analytic on the open unit
disk, and is given by
of this function is also analytic on the open unit
disk, and is given by
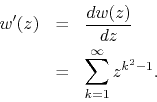
The non-differentiability of the function ![]() on the unit circle must
therefore be related to the non-existence of the
on the unit circle must
therefore be related to the non-existence of the ![]() limits of the
function
limits of the
function ![]() from within the unit disk. Note that in terms of
derivatives with respect to
from within the unit disk. Note that in terms of
derivatives with respect to ![]() we may write
we may write
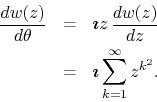
This relation holds true everywhere within the open unit disk. One might
therefore consider analyzing the differentiability of
![]() and
and
![]() on the unit circle by
examining the behavior of the
on the unit circle by
examining the behavior of the ![]() limits of the function
limits of the function
![]() , which is proportional to the logarithmic derivative of
, which is proportional to the logarithmic derivative of ![]() .
The expectation is that the function
.
The expectation is that the function ![]() has a densely distributed
countable infinity of borderline soft singularities over the unit circle.
It then follows that its logarithmic derivative has a densely distributed
countable infinity of borderline hard singularities over the unit circle,
and therefore fails to be defined at all points. This can be understood as
a consequence of the extended version of Abel's theorem [6],
so long as it can be shown that the series diverges to infinity everywhere
over the unit circle.
has a densely distributed
countable infinity of borderline soft singularities over the unit circle.
It then follows that its logarithmic derivative has a densely distributed
countable infinity of borderline hard singularities over the unit circle,
and therefore fails to be defined at all points. This can be understood as
a consequence of the extended version of Abel's theorem [6],
so long as it can be shown that the series diverges to infinity everywhere
over the unit circle.
The Riemann sine series has been widely studied [7], but its FC series less so, it would seem. There are many papers and results about lacunary functions related to lacunary power series [8], which could be of use here. In particular the Fabry and the Ostrowski-Hadamard gap theorems [9] seem to be directly relevant. Such a lacunary function can be characterized as one that cannot be analytically continued beyond the boundary of the maximum disk of convergence of its Taylor series. This would be the case if such a function had a densely distributed set of singularities over the unit circle. Note that using the correspondence established in this paper we may construct from any lacunary trigonometric series a corresponding lacunary power series, and vice-versa, so that these two subjects are completely identified with each other.