Next: A Modified Ratio Test Up: Some Basic Convergence Results Previous: Strong Convergence
The situation in the strong convergence case suggests the following strong convergence test for an arbitrary DP Fourier series. Given for example a cosine series, and the corresponding FC series, one may write down the pair of extended series
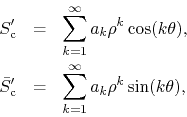
where ![]() is real. If it can be established that there is a
single point, with
is real. If it can be established that there is a
single point, with ![]() and any value of
and any value of ![]() , such that these
series are both convergent at that point, then the original cosine series
converges strongly to a
, such that these
series are both convergent at that point, then the original cosine series
converges strongly to a ![]() function over its whole domain, that
is, the whole periodic interval. The values
function over its whole domain, that
is, the whole periodic interval. The values ![]() and
and ![]() are sensible choices for the test, because the sine series is always
convergent for these values, so that only the cosine series has to be
actually tested. The same test holds if we start with a sine series, of
course. Additionally, the corresponding FC series are also strongly
convergent everywhere on the periodic interval to the respective FC
functions.
are sensible choices for the test, because the sine series is always
convergent for these values, so that only the cosine series has to be
actually tested. The same test holds if we start with a sine series, of
course. Additionally, the corresponding FC series are also strongly
convergent everywhere on the periodic interval to the respective FC
functions.
This same test can also be used to determine whether the given series is
strongly divergent, if we revert the condition on ![]() and use the test
with
and use the test
with ![]() , looking now for a point of divergence. In this case it is
enough that any one of the two DP trigonometric series of the FC pair
diverge at a single point in the interior of the unit disk to ensure that
both diverge almost everywhere over the unit circle.
, looking now for a point of divergence. In this case it is
enough that any one of the two DP trigonometric series of the FC pair
diverge at a single point in the interior of the unit disk to ensure that
both diverge almost everywhere over the unit circle.